fgoalattainРассмотрите возможность проектирования фильтра с линейно-фазовой конечной импульсной характеристикой (FIR). Задача состоит в том, чтобы сконструировать фильтр нижних частот с величиной 1 на всех частотах между 0 и 0,1 Гц и величиной 0 между 0,15 и 0,5 Гц.
Частотный отклик H (f) для такого фильтра определяется
| =∑n=0M−1a (n) cos (2.dfn), | (1) |
где A (f) - величина частотной характеристики. Одним из решений является применение метода достижения цели к величине частотной характеристики. Учитывая функцию, которая вычисляет величину ,fgoalattain будет пытаться изменять коэффициенты a (n) величины до тех пор, пока отклик величины не совпадет с требуемым откликом в пределах некоторого допуска. Функция, которая вычисляет отклик величины, приведена вfiltmin.m. Эта функция использует aкоэффициенты функции величины и wдискретизация интересующей частотной области.
Чтобы настроить задачу достижения цели, необходимо указать goal и weights для проблемы. Для частот от 0 до 0,1 цель равна единице. Для частот от 0,15 до 0,5 цель равна нулю. Частоты от 0,1 до 0,15 не указаны, поэтому цели или веса в этом диапазоне не нужны.
Эта информация хранится в переменной goal передано в fgoalattain. Длина goal совпадает с длиной, возвращаемой функцией filtmin. Чтобы цели были одинаково удовлетворены, обычно weight будет установлено значение abs(goal). Однако, поскольку некоторые из целей равны нулю, эффект от использования weight=abs(goal) будет форсировать цели с weight 0, чтобы быть удовлетворенными как жесткие ограничения, и цели с weight 1, возможно, недостигнут (см. Метод достижения цели). Потому что все цели близки по величине, используя weight единство для всех целей придаст им равный приоритет. (Использование abs(goal) для весов важнее, когда величина goal отличается более существенно.) Также, настройка
options = optimoptions('fgoalattain','EqualityGoalCount',length(goal)); указывает, что каждая цель должна быть как можно ближе к ее целевому значению (не больше и не меньше).
function y = filtmin(a,w) n = length(a); y = cos(w'*(0:n-1)*2*pi)*a ;
% Plot with initial coefficients
a0 = ones(15,1);
incr = 50;
w = linspace(0,0.5,incr);
y0 = filtmin(a0,w);
clf, plot(w,y0,'-.b');
drawnow;
% Set up the goal attainment problem
w1 = linspace(0,0.1,incr) ;
w2 = linspace(0.15,0.5,incr);
w0 = [w1 w2];
goal = [1.0*ones(1,length(w1)) zeros(1,length(w2))];
weight = ones(size(goal));
% Call fgoalattain
options = optimoptions('fgoalattain','EqualityGoalCount',length(goal));
[a,fval,attainfactor,exitflag]=fgoalattain(@(x)filtmin(x,w0),...
a0,goal,weight,[],[],[],[],[],[],[],options);
% Plot with the optimized (final) coefficients
y = filtmin(a,w);
hold on, plot(w,y,'r')
axis([0 0.5 -3 3])
xlabel('Frequency (Hz)')
ylabel('Magnitude Response (dB)')
legend('initial', 'final')
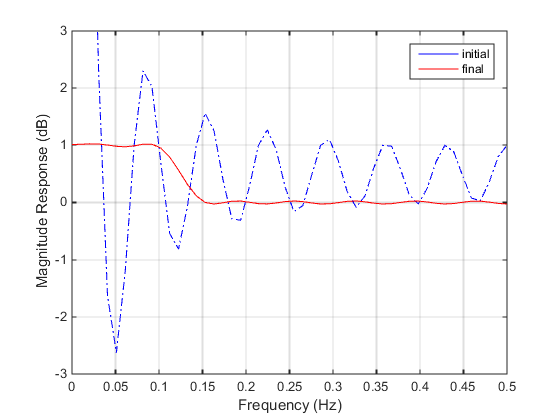
grid onСравните отклик величины, вычисленный с начальными коэффициентами, и конечные коэффициенты (отклик величины с коэффициентами начальной и конечной величины). Обратите внимание, что вы можете использовать firpm(Панель инструментов обработки сигналов) в программном обеспечении Toolbox™ обработки сигналов для проектирования этого фильтра.
Отклик на величину с начальными и конечными коэффициентами величины