solvepde возвращает StationaryResults или TimeDependentResults объект, свойства которого содержат решение и его градиент в узлах сети. Можно интерполировать решение и его градиент в другие точки геометрии с помощью interpolateSolution и evaluateGradient. Можно также вычислить поток решения в узлах сетки и в произвольных точках с помощью evaluateCGradient.
Примечание
solvepde не вычисляет компоненты потока раствора PDE. Чтобы вычислить поток решения в узлах сетки, используйте evaluateCGradient.
solvepdeeig возвращает EigenResults объект, свойства которого содержат собственные векторы решения, рассчитанные в узлах сетки. Можно интерполировать решение на другие точки с помощью interpolateSolution.
Размеры раствора, его градиент и поток раствора зависят от:
Количество точек геометрической оценки.
Для результатов, возвращенных solvepde или solvepdeeig, это количество узлов сети.
Для результатов, возвращенных interpolateSolution,evaluateGradient, и evaluateCGradient это количество точек запроса.
Количество уравнений.
Для результатов, возвращенных solvepde или solvepdeeig, это количество уравнений в системе.
Для результатов, возвращенных interpolateSolution,evaluateGradient, и evaluateCGradient, это число индексов уравнений запроса.
Количество раз для зависящей от времени задачи или количество режимов для задачи собственного значения.
Для результатов, возвращенных solvepde, это количество раз решения (указанное как вход в solvepde).
Для результатов, возвращенных solvepdeeig, это количество собственных значений.
Для результатов, возвращенных interpolateSolution, evaluateGradient, и evaluateCGradient, это количество раз запроса для зависящих от времени проблем или режимов запроса для проблем собственных значений.
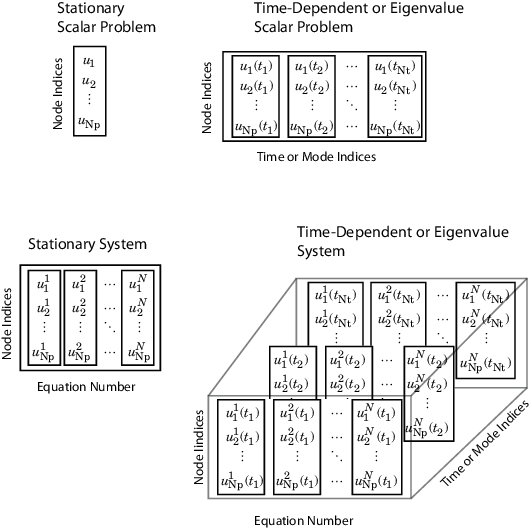
Предположим, у вас есть проблема, в которой:
Np - количество узлов в сетке.
Nt - количество раз для зависящей от времени задачи или количество режимов для задачи собственного значения.
N - количество уравнений в системе.
Предположим, что вы также вычисляете решение, его градиент или поток решения в других точках («точки запроса») в геометрии, используя interpolateSolution, evaluateGradient, или evaluateCGradientсоответственно. Здесь:
Nqp - количество точек запроса.
Nqt - количество раз запроса для зависящей от времени задачи или количество режимов запроса для задачи собственного значения.
Nq - количество индексов уравнений запросов.
В таблицах показано, как индексировать в решение, возвращаемое solvepde или solvepdeeig, где:
iP содержит индексы узлов.
iT содержит индексы времени для зависящей от времени задачи или номера режимов для задачи собственного значения.
iN содержит индексы уравнений.
В таблицах также показаны размеры решений, градиенты и поток решения в узловых местоположениях (возвращаемые solvepde,solvepdeeig, и evaluateCGradient) и размеры интерполированных решений и градиентов (возвращаемые interpolateSolution, evaluateGradient, и evaluateCGradient).
| Проблема стационарного PDE | Решение доступа и компоненты градиента | Размер NodalSolution, XGradients, YGradients, ZGradientsи компоненты потока в узловых точках | Размер решения, компоненты градиента и компоненты потока в точках запроса |
|---|---|---|---|
| Скаляр |
| Np-по-1 | Nqp-по-1 |
Система, N > 1 |
| Npоколо-N | Nqpоколо-N |
| Зависящая от времени проблема PDE | Решение доступа и компоненты градиента | Размер NodalSolution, XGradients, YGradients, ZGradientsи компоненты потока в узловых точках | Размер решения, компоненты градиента и компоненты потока в точках запроса |
|---|---|---|---|
| Скаляр |
| Npоколо-Nt | Nqpоколо-Nqt |
Система, N > 1 |
| Npоколо-Nоколо-Nt | Nqpоколо-Nqоколо-Nqt |
| Проблема собственного значения PDE | Доступ к собственным векторам | Размер Eigenvectors | Размер интерполированных собственных векторов |
|---|---|---|---|
| Скаляр |
| Npоколо-Nt | Nqpоколо-Nqt |
Система, N > 1 |
| Npоколо-Nоколо-Nt | Nqpоколо-Nqоколо-Nqt |
EigenResults | evaluateGradient | interpolateSolution | solvepde | solvepdeeig | StationaryResults | TimeDependentResults