Моделирование динамики трехфазной круглороторной или явно полюсной синхронной машины с использованием стандартных параметров в блоках pu
Simscape / Электрический / Специализированные Энергосистемы / Электрические Машины
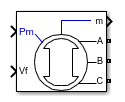
Блок Synchronous Machine pu Standard моделирует синхронную машину в режиме генератора или двигателя с использованием стандартных параметров в единицах pu. Режим работы диктуется признаком механической мощности (положительной для режима генератора или отрицательной для режима двигателя). Электрическая часть машины представлена моделью пространства состояния шестого порядка, а механическая часть такая же, как в блоке упрощенной синхронной машины.
Модель учитывает динамику обмоток статора, поля и демпфера. Эквивалентная схема модели представлена в опорной рамке ротора (qd-рамке). Обмотки статора соединены трепом с внутренней нейтральной точкой. Все параметры ротора и электрические величины просматриваются со статора и идентифицируются по заполненным переменным. Подстрочные индексы:
d, q - количество по осям d- и q
R, s - Количество ротора и статора
l, m - Индуктивность утечки и намагничивания
f, k - Количество обмоток возбуждения и демпфера
Электрическая модель машины показана на этих схемах.
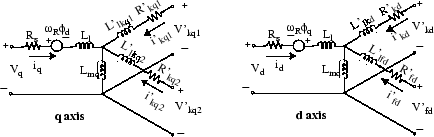
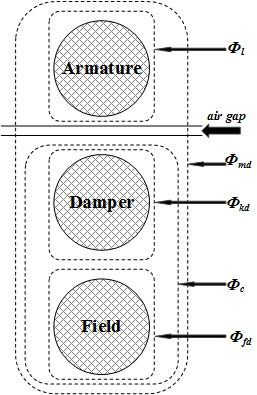
Традиционная теория синхронного моделирования машин для анализа устойчивости предполагает, что взаимные индуктивности между якорем, демпфером и полем на обмотках с прямой осью идентичны. Обычно обмотки демпфера находятся вблизи воздушного зазора, и в результате схемы демпфера, связывающие поток, почти равны якорю, связывающему поток. Эта гипотеза дает приемлемые результаты для широкого спектра исследований стабильности, особенно на стороне сети. Однако, когда речь идет о текущих полевых исследованиях, существует значительная ошибка. Эквивалентная схемная динамическая модель синхронной машины может включать в себя дополнительную индуктивность, представляющую разность между взаимными индуктивами «поле-демпфер» и «поле-якорь» на оси D [1]. Эта индуктивность обычно называется индуктивностью Каная. Индуктивность Каная соответствует потоку утечки, ФС, на следующем рисунке и интерпретируется как корректирующий элемент в эквивалентной модели, который может иметь отрицательное значение [2].
В стандарте IEEE 1110-2002 [3] представлены прямые и квадратичные оси динамической модели синхронной машины, как показано на диаграммах.
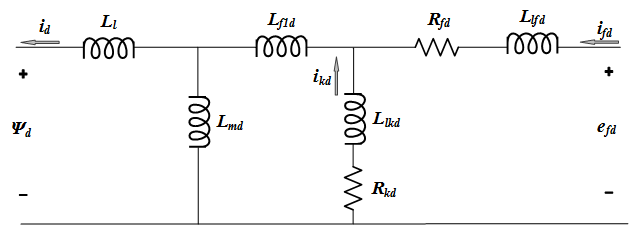
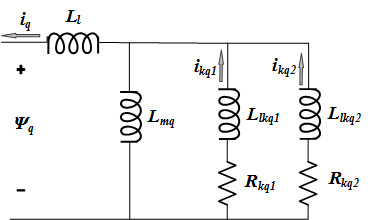
Соответствующими уравнениями являются:
В дискретных системах при установке для параметра модели дискретного решателя блока синхронной машины значения Trapezoidal non iterative, возможно, вам придется подключить небольшую паразитную резистивную нагрузку на клеммах машины, чтобы избежать цифровых колебаний. Большие времена выборки требуют больших нагрузок. Минимальная резистивная нагрузка пропорциональна времени выборки. Как правило, следует помнить, что с шагом времени 25 мкс в системе с частотой 60 Гц минимальная нагрузка составляет приблизительно 2,5% от номинальной мощности машины. Например, синхронная машина 200 МВА в энергосистеме, дискретизированная с временем выборки 50 мкс, требует приблизительно 5% резистивной нагрузки или 10 МВт. Если время выборки уменьшено до 20 мкс, достаточно резистивной нагрузки 4 МВт.
Однако если для параметра модели дискретного решателя блока синхронной машины задано значение Trapezoidal iterative (alg. loop), можно использовать ничтожно малую паразитную нагрузку (ниже 0,1% номинальной мощности) при сохранении численной устойчивости. Эта итеративная модель создает алгебраический цикл и приводит к более низкой скорости моделирования.
Укажите стандартные параметры, также известные как рабочие параметры, синхронной машины (такие как стационарные, переходные и/или субтрансцентные реактивы и временные константы) в качестве входных данных блока. Как правило, производители машин обеспечивают рабочие параметры.
В программном обеспечении анализа энергосистемы синхронные машинные уравнения обычно решаются с использованием метода прямого квадратурного нулевого преобразования. Метод трансляции данных вычисляет фундаментальные параметры из стандартных параметров [2], [3].
Preset model - Электрические и механические параметрыNo (по умолчанию) | 01: 50Hz 400V 8.1kVA 1500RPM | 02: 50Hz 400V 16kVA 1500RPM | ...Набор заданных электрических и механических параметров для различных номинальных значений мощности синхронной машины (кВА), межфазного напряжения (В), частоты (Гц) и номинальной частоты вращения (об/мин).
Выберите одну из предустановленных моделей для загрузки соответствующих электрических и механических параметров. Возможны следующие варианты:
01: 50Hz 400V 8.1kVA 1500RPM
02: 50Hz 400V 16kVA 1500RPM
03: 50Hz 400V 31.3kVA 1500RPM
04: 50Hz 400V 42.5kVA 1500RPM
05: 50Hz 400V 60kVA 1500RPM
06: 50Hz 400V 85kVA 1500RPM
07: 50Hz 400V 250kVA 1500RPM
08: 50Hz 400V 325kVA 1500RPM
09: 50Hz 400V 670kVA 1500RPM
10: 50Hz 400V 910kVA 1500RPM
11: 50Hz 400V 1320kVA 1500RPM
12: 50Hz 400V 2000kVA 1500RPM
13: 60Hz 460V 10.2kVA 1800RPM
14: 60Hz 460V 20kVA 1800RPM
15: 60Hz 460V 37.5kVA 1800RPM
16: 60Hz 460V 52.5kVA 1800RPM
17: 60Hz 460V 72.5kVA 1800RPM
18: 60Hz 460V 100kVA 1800RPM
19: 60Hz 460V 300kVA 1800RPM
20: 60Hz 460V 406kVA 1800RPM
21: 60Hz 460V 800kVA 1800RPM
22: 60Hz 460V 1075kVA 1800RPM
23: 60Hz 460V 1588kVA 1800RPM
24: 60Hz 460V 2500kVA 1800RPM
Выбрать No (по умолчанию), если не требуется использовать предустановленную модель или требуется изменить некоторые параметры предустановленной модели, как описано ниже.
При выборе заданной модели электрические и механические параметры на вкладке Параметры (Parameters) становятся недоступными. Чтобы начать работу с предварительно заданной модели и затем изменить параметры машины, выполните следующие действия.
Выберите предустановленную модель, которую требуется инициализировать.
Измените значение параметра «Предустановленная модель» на No. Это действие не изменяет параметры машины, но разрывает соединение с предварительно установленной моделью.
Измените необходимые параметры машины.
Mechanical input - Механический вводMechanical power Pm (по умолчанию) | Speed w | Mechanical rotational portСледует ли представлять механическую мощность, прикладываемую к валу, или частоту вращения ротора в качестве входного сигнала Simulink ® блока, или представлять вал машины с Simscape™ вращательным механическим портом.
Выбрать Mechanical power Pm чтобы указать механический вход питания в pu и открыть порт Pm. Скорость машины определяется постоянной инерции Н и разностью между механическим крутящим моментом Tm, который является результатом приложенной механической мощности Pm, и внутренним электромагнитным крутящим моментом Те. Когда скорость положительная, положительный сигнал механической мощности указывает режим генератора, а отрицательный сигнал указывает режим двигателя.
Выбрать Speed w для указания скорости входа в pu и открытия порта w. Скорость машины накладывается и механическая часть модели (постоянная инерции H) игнорируется. Использование скорости в качестве механического ввода позволяет моделировать механическую связь между двумя машинами.
На следующем рисунке показано, как моделировать жесткое соединение вала в двигателе-генераторе, где обе машины являются синхронными машинами.
Выход скорости машины 1 (двигателя) соединен со входом скорости машины 2 (генератора). На этом чертеже крутящий момент трения игнорируется в машине 2. Следовательно, его электромагнитный крутящий момент Te соответствует механическому крутящему моменту Tm, приложенному к валу машины 1. Соответствующая механическая входная мощность машины 1 вычисляется как Pm = Tm * w. Коэффициент Kw учитывает единицы скорости обеих машин (pu) и передаточное число коробки передач w2/w1. Коэффициент KT учитывает блоки крутящего момента обеих машин (pu) и номинальные значения машин. Кроме того, поскольку инерция J2 игнорируется в машине 2, J2 относится к скорости машины 1 и должна быть добавлена к инерции машины 1, J1.
Выбрать Mechanical rotational port для открытия механического поворотного порта Simscape, S, который позволяет соединять вал машины с другим валом машины или с другими блоками Simscape, имеющими механические поворотные порты.
На рисунке показано, как подключить блок источника идеального крутящего момента из библиотеки Simscape к порту вала машины, чтобы представить машину в режиме двигателя или генератора, когда частота вращения ротора положительная.
Rotor type - Тип ротораSalient-pole (по умолчанию) | RoundУкажите тип ротора: Salient-pole или Round (цилиндрический). Настройка влияет на количество цепей ротора на оси q (обмотки демпфера).
Use signal names to identify bus labels - Как идентифицировать метки шиныoff (по умолчанию) | onЕсли этот флажок установлен, на выходе измерения используются имена сигналов для идентификации меток шины. Эта опция используется для приложений, для которых метки сигналов шины должны содержать только буквенно-цифровые символы.
Если флажок снят, на выходе измерения используется определение сигнала для идентификации меток шины. Метки содержат неальфанумерные символы, несовместимые с некоторыми приложениями Simulink.
Nominal power, line-to-line voltage, frequency [ Pn(VA) Vn(Vrms) fn(Hz) ] - Номинальная мощность, межлинейное напряжение и частота[6e+04 400 50] (по умолчанию) | трехэлементный векторОбщая трехфазная кажущаяся мощность (VA), среднеквадратичное напряжение (pu), частота (Hz) и ток поля (pu).
Этот параметр идентичен параметру номинальной мощности, напряжения, частоты, тока поля [Pn (VA) Vn (Vrms) fn (Hz) ifn (A)] основного блока синхронной машины SI, за исключением того, что номинальный ток поля не указан. Это значение не требуется, так как блок Synchronous Machine pu Standard не нуждается в коэффициенте преобразования. Поскольку количества роторов рассматриваются из статора, они преобразуются в pu с использованием величин основания статора, полученных из предыдущих трех номинальных параметров.
Reactances [ Xd Xd' Xd'' Xq Xq'' Xl ] (pu) - Реактивные сопротивления[2.24 0.17 0.12 1.02 0.13 0.08] (по умолчанию) | шестиэлементный векторсинхронное реактивное сопротивление Xd по оси d, переходное реактивное сопротивление Xd 'и вычитаемое реактивное сопротивление Xd "; синхронное реактивное сопротивление Xq по оси q и субтрансцентное реактивное сопротивление Xq "; и реактивность Х1 утечки (все в pu).
Чтобы включить этот параметр, установите тип ротора в Salient-pole.
Reactances [ Xd Xd' Xd'' Xq Xq' Xq'' Xl ] (pu) - Реактивные сопротивления[ 1.81, 0.3, 0.23, 1.76, 0.65, 0.25, 0.15 ] (по умолчанию)синхронное реактивное сопротивление Xd по оси d, переходное реактивное сопротивление Xd 'и вычитаемое реактивное сопротивление Xd "; синхронное реактивное сопротивление Xq по оси q, переходное реактивное сопротивление Xq 'и субтрансцентное реактивное сопротивление Xq "; и реактивность Х1 утечки (все в pu).
Чтобы включить этот параметр, установите тип ротора в Round.
d axis - постоянная времени по d-осиShort-circuit (по умолчанию) | Open-circuitПостоянная времени для оси d.
q axis - постоянная времени по оси qShort-circuit (по умолчанию) | Open-circuitПостоянная времени для оси q.
[ Tdo' Tdo'' Tqo'' ] (s) - Временные константы в с[ 4.4849 0.0681 0.1 ] (по умолчанию) | трехэлементный векторКонстанты времени, все в s, для следующего:
d-осевая переходная разомкнутая цепь (Tdo ')
d-ось вычитание разомкнутой цепи (Tdo ")
q-ось вычитание разомкнутой цепи (Tqo ")
Чтобы включить этот параметр, установите тип ротора в Salient-pole, ось d к Open-circuitи ось q к Open-circuit.
[ Tdo' Tdo'' Tqo' Tqo'' ] (s) - Временные константы в с[ 8.0, 0.03, 1.0, 0.07 ] (по умолчанию) | четырехэлементный векторКонстанты времени, все в s, для следующего:
d-осевая переходная разомкнутая цепь (Tdo ')
d-ось вычитание разомкнутой цепи (Tdo ")
q-осевая переходная разомкнутая цепь (Tqo ')
q-ось вычитание разомкнутой цепи (Tqo ")
Чтобы включить этот параметр, установите тип ротора в Round, ось d к Open-circuitи ось q к Open-circuit.
[ Tdo' Tdo'' Tq'' ] (s) - Временные константы в с[ 4.49 0.0681 0.0513 ] (по умолчанию) | трехэлементный векторКонстанты времени, все в s, для следующего:
d-осевая переходная разомкнутая цепь (Tdo ')
d-ось вычитание разомкнутой цепи (Tdo ")
q-осевое вычитание короткого замыкания (Tq ")
Чтобы включить этот параметр, установите тип ротора в Salient-pole, ось d к Open-circuitи ось q к Short-circuit.
[ Tdo' Tdo'' Tq' Tq'' ] (s) - Временные константы в с[ 8.0, 0.03, 0.3371, 0.0295 ] (по умолчанию) | четырехэлементный векторКонстанты времени, все в s, для следующего:
d-осевая переходная разомкнутая цепь (Tdo ')
d-ось вычитание разомкнутой цепи (Tdo ")
q-осевое переходное короткое замыкание (Tq ')
q-осевое вычитание короткого замыкания (Tq ")
Чтобы включить этот параметр, установите тип ротора в Round, ось d к Open-circuitи ось q к Short-circuit.
[ Td' Td'' Tqo'' ] (s) - Временные константы в с[ 1.01, 0.053, 0.1 ] (по умолчанию) | трехэлементный векторКонстанты времени, все в s, для следующего:
d-осевое переходное короткое замыкание (Td ')
Вычитаемое короткое замыкание по оси d (Td ")
q-ось вычитание разомкнутой цепи (Tqo ")
Чтобы включить этот параметр, установите тип ротора в Salient-pole, ось d к Short-circuitи ось q к Open-circuit.
[ Td' Td'' Tqo' Tqo'' ] (s) - Временные константы в с[ 1.3201, 0.023, 1.0, 0.07 ] (по умолчанию) | четырехэлементный векторКонстанты времени, все в s, для следующего:
d-осевое переходное короткое замыкание (Td ')
Вычитаемое короткое замыкание по оси d (Td ")
q-осевая переходная разомкнутая цепь (Tqo ')
q-ось вычитание разомкнутой цепи (Tqo ")
Чтобы включить этот параметр, установите тип ротора в Round, ось d к Short-circuitи ось q к Open-circuit.
[ Td' Td'' Tq'' ] (s) - Временные константы в с[0.012 0.003 0.003] (по умолчанию) | трехэлементный векторКонстанты времени, все в s, для следующего:
d-осевое переходное короткое замыкание (Td ')
Вычитаемое короткое замыкание по оси d (Td ")
q-осевое вычитание короткого замыкания (Tq ")
Чтобы включить этот параметр, установите тип ротора в Salient-pole, ось d к Short-circuitи ось q к Short-circuit.
[ Td' Td'' Tq' Tq'' ] (s) - Временные константы в с[ 1.3201, 0.0231, 0.3371, 0.0295 ] (по умолчанию) | четырехэлементный векторКонстанты времени, все в s, для следующего:
d-осевое переходное короткое замыкание (Td ')
Вычитаемое короткое замыкание по оси d (Td ")
q-осевое переходное короткое замыкание (Tq ')
q-осевое вычитание короткого замыкания (Tq ")
Чтобы включить этот параметр, установите тип ротора в Round, ось d к Short-circuitи ось q к Short-circuit.
Stator resistance Rs (pu) - Сопротивление статора0.037875 (по умолчанию) | положительный скалярСопротивление статора Rs, в pu.
Inertia coefficient, friction factor, pole pairs [ H(s) F(pu) p()] - коэффициент инерции, коэффициент трения и пары полюсов;[0.1028 0.02056 2] (по умолчанию) | трехэлементный векторПостоянная инерции H (s), которая является отношением энергии, накопленной в роторе при номинальной скорости, к номинальной мощности машины, коэффициенту трения F (крутящий момент pu/скорость pu) и числу пар полюсов p. Крутящий момент трения Tf пропорционален частоте вращения ротора (Tf = F.λ, где все величины выражены в pu).
Чтобы включить этот параметр, установите параметр «Механический ввод» в значение Mechanical power Pm или Mechanical rotational port.
Pole pairs p () - пары полюсов20 (по умолчанию) | положительное целое числоКоличество пар полюсов синхронной машины.
Чтобы включить этот параметр, установите параметр «Механический ввод» в значение Speed w.
Initial conditions [ dw(%) th(deg) ia,ib,ic(pu) pha,phb,phc(deg) Vf(pu) ] - Исходные условия[ 0 0 0 0 0 0 0 0 1 ] (по умолчанию) | девятиэлементный векторНачальное отклонение Δλ скорости (в процентах от номинальной скорости), электрический угол ротора (в градусах), значения тока линии ia, ib, ic (pu) и фазовые углы pha, phb, phc (в градусах) и начальное напряжение поля Vf (pu). Эти значения можно вычислить автоматически с помощью инструмента Поток нагрузки (Load Flow) или инструмента Инициализация станка (Machine Initialization) блока powergui.
Simulate saturation - Имитация магнитного насыщенияon (по умолчанию) | offИмитируется ли магнитное насыщение ротора и статорного утюга.
Установите этот флажок, чтобы предоставить матрицу параметров для моделирования насыщения.
Снимите этот флажок, чтобы не допустить насыщения модели в моделировании. В этом случае соотношение между ifd и Vt является линейным (без насыщения).
[ ifd; vt] (pu) - Параметры кривой насыщения без нагрузки[0.6404,0.7127,0.8441,0.9214,0.9956,1.082,1.19,1.316,1.457;0.7,0.7698,0.8872,0.9466,0.9969,1.046,1.1,1.151,1.201] (по умолчанию) | векторПараметры кривой насыщения без нагрузки. Магнитное насыщение статора и роторного утюга моделируется кусочно-линейной зависимостью, определяющей точки на кривой насыщения без нагрузки. Первая строка этой матрицы содержит значения токов поля (в pu). Второй ряд содержит значения соответствующих клеммных напряжений (в pu). Первая точка (первый столбец матрицы) должна отличаться от [0,0]. Эта точка соответствует точке, где начинается эффект насыщения. Для насыщения номинальный ток поля и номинальное среднеквадратичное напряжение линии к линии являются базовыми значениями для тока поля и напряжения клеммы соответственно.
Щелкните График (Plot), чтобы просмотреть кривую насыщения без нагрузки.
Чтобы включить этот параметр, выберите «Моделирование насыщения».
Чтобы включить вкладку Дополнительно (Advanced), в блоке powergui установите для параметра Тип моделирования (Simulation type) значение Discrete и снимите флажок Автоматически обрабатывать дискретный решатель.
Sample time (-1 for inherited) - Время отбора проб для блока-1 (по умолчанию) | скалярВремя выборки, используемое блоком. Чтобы наследовать время выборки, указанное в блоке powergui, установите для этого параметра значение −1.
Discrete solver model - Метод интеграцииTrapezoidal non iterative (по умолчанию) | Trapezoidal iterative (alg. loop) | Trapezoidal robust | Backward Euler robustМетод интеграции, используемый блоком, если для параметра типа Solver блока powergui установлено значение Discrete.
Для модели дискретного решателя автоматически устанавливается значение Trapezoidal robust при выборе параметров Автоматически обрабатывать дискретный решатель и Дополнительные настройки решателя блоков блока powergui.
Trapezoidal non iterative и Trapezoidal iterative (alg. loop) методы больше не рекомендуются для дискретизации блока Synchronous Machine pu Standard. Trapezoidal non iterative требуется добавить незначительные шунтирующие нагрузки на клеммы станка, чтобы гарантировать стабильность моделирования, и Trapezoidal iterative (alg. loop) может не сойтись и вызвать остановку моделирования при увеличении количества машин в модели.
Trapezoidal robust и Backward Euler robust методы позволяют исключить необходимость использования паразитных нагрузок и моделировать машину без нагрузок. Для исключения топологических ошибок машин, подключенных к индуктивной цепи (например, автоматический выключатель, соединенный последовательно с машиной); машина моделирует незначительную внутреннюю нагрузку 0,01% номинальной мощности.
Trapezoidal robust метод несколько точнее, чем Backward Euler robust способ, особенно когда модель моделируется в большие времена выборки. Trapezoidal robust способ может производить небольшие демпфированные числовые колебания на напряжении машины в условиях холостого хода, а Backward Euler robust способ предотвращает колебания и поддерживает хорошую точность.
Дополнительные сведения о том, какой метод следует использовать в приложении, см. в разделе Моделирование дискретизированных электрических систем.
Параметры потока нагрузки используются для определения параметров блока для использования с инструментом «Поток нагрузки» блока powergui. Эти параметры потока нагрузки используются только для инициализации модели. Они не влияют ни на модель блока, ни на производительность моделирования.
Generator type - Тип машинного генератораPV (по умолчанию) | swing | PQТип генератора машины. Выбор:
swing - реализует генератор, контролирующий величину и фазовый угол его напряжения на клемме. Величина и угол опорного напряжения определяются параметрами напряжения шины Swing или шины PV и угла напряжения шины Swing блока шины Load Flow, подключенного к клеммам машины.
PV - Реализует генератор, управляющий его выходной активной мощностью P и величиной напряжения V. P задается параметром активной выработки мощности P (W) блока. V определяется параметром напряжения шины качания или шины PV блока шины потока нагрузки, подключенного к клеммам машины. Можно управлять минимальной и максимальной реактивной мощностью, генерируемой блоком, с помощью параметров Минимальная реактивная мощность Qmin (var) и Максимальная реактивная мощность Qmax (var).
PQ - Реализует генератор, контролирующий его выходную активную мощность P и реактивную мощность Q. P и Q задаются параметрами активной выработки мощности P (W) и реактивной выработки мощности Q (var) блока соответственно.
Active power generation P (W) - Активная мощность, вырабатываемая машиной0 (по умолчанию) | скалярАктивная мощность, генерируемая машиной, в ваттах. При работе машины в режиме двигателя указывается отрицательное значение.
Чтобы включить этот параметр, задайте для параметра Тип генератора значение PV или PQ.
Reactive power generation Q (var) - Реактивная мощность, вырабатываемая машиной0 (по умолчанию) | скалярРеактивная мощность, генерируемая машиной, в vars. Отрицательное значение указывает на то, что реактивная мощность поглощается машиной.
Чтобы включить этот параметр, задайте для параметра Тип генератора значение PQ.
Minimum reactive power Qmin (var) - Минимальная реактивная мощность, вырабатываемая машиной-inf (по умолчанию) | скалярМинимальная реактивная мощность, которая может быть сгенерирована машиной при поддержании напряжения на клемме на ее опорном значении. Это опорное напряжение определяется параметром напряжения шины качания или шины PV блока шины потока нагрузки, подключенного к клеммам машины. Значение по умолчанию: -inf, что означает отсутствие нижнего предела на выходе реактивной мощности.
Чтобы включить этот параметр, задайте для параметра Тип генератора значение PV.
Maximum reactive power Qmax (var) - Максимальная реактивная мощность, вырабатываемая машинойinf (по умолчанию) | скалярМаксимальная реактивная мощность, которая может быть сгенерирована машиной при поддержании напряжения на клемме на ее опорном значении. Это опорное напряжение определяется параметром напряжения шины качания или шины PV блока шины потока нагрузки, подключенного к клеммам машины. Значение по умолчанию: inf, что означает отсутствие верхнего предела на выходе реактивной мощности.
Чтобы включить этот параметр, задайте для параметра Тип генератора значение PV.
power_thermal В примере используется блок Synchronous Machine pu Standard для моделирования субсинхронизированного резонанса (SSR) в паровой турбине и регуляторе в сети с последовательной компенсацией.
[1] Канай, И.М. «Причины расхождений при расчете количества ротора и точных эквивалентных диаграмм синхронной машины». Транзакции IEEE ® по устройствам и системам питания. PAS-88, № 7 (1969): 1114-1120.
[2] Moeini, A., et al. «Синхронная модель Machine Stability, Обновление Метода Перевода Данных о Станд. IEEE 1110-2002». Сеансы панели стандартов IEEE. 2018.
[3] Руководство IEEE по методам моделирования синхронных генераторов и их применению при анализе стабильности энергосистемы. IEEE Std 1110-2002 (Редакция IEEE Std 1110-1991 [2003]): 1-72.
[4] Краузе, P.C. Анализ электрических машин. Раздел 12.5. Нью-Йорк: Макгроу-Хилл, 1986.
[5] Kundur, P. Стабильность и управление энергосистемой. Нью-Йорк, Макгроу-Хилл, 1994.
Система возбуждения | Гидравлическая турбина и регулятор | powergui | Упрощенная синхронная машина | Паровая турбина и регулятор | Синхронная машина pu Основные | Основные принципы SI синхронной машины