Синхронный двигатель постоянного магнита, определяемый в терминах связи магнитного потока
Simscape/Электрический/Электромеханический/Постоянный магнит
FEM-параметризованный блок PMSM реализует модель синхронного двигателя постоянного магнита (PMSM), определенную в терминах связи магнитного потока. Параметризация блока осуществляется путем предоставления табличных данных магнитного потока двигателя как функции тока и угла ротора. Так обычно экспортируют информацию о потоке сторонние пакеты магнитного метода конечных элементов (КЭМ). Из-за табличной формы поток может изменяться нелинейно как по углу ротора, так и по току. Поэтому этот блок можно использовать для моделирования PMSM с трапециевидным профилем обратной ЭДС, иногда называемым бесщеточным двигателем постоянного тока, а также обычной PMSM.
На рисунке показана эквивалентная схема для wye-connected PMSM. Когда поток постоянного магнита совмещается с магнитной осью А-фазы, угол ротора равен нулю.
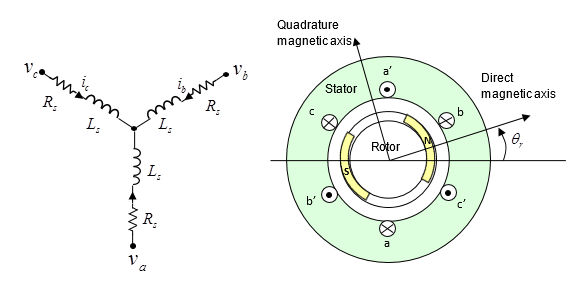
На практике поток, связывающий каждую из трех обмоток, зависит от всех трех токов и угла поворота ротора. Табулирование потока как функции четырех независимых переменных может привести к неэффективности моделирования и значительным требованиям к памяти для управления данными. Таким образом, блок позволяет выбрать один из следующих методов параметризации для потока и крутящего момента:
2-D данные частных производных - 2-D табличный поиск, с опциями для табуляции в терминах тока и угла ротора, или в терминах d-axis и q- осевые токи. Первый вариант предполагает постоянную взаимную индуктивность и поддерживает несинусоидальные задние emf-профили. Второй вариант предполагает синусоидальную обратную emf и фиксирует эффекты насыщения для внутренних PMSM (IPMSM).
3D данные о частной производной - 3D поиск по таблице, на основе постоянного тока, квадратурного тока и угла ротора. Предоставляются данные поиска потока для фазы. Блок использует преобразование Park для отображения трех токов обмотки статора на прямые и квадратурные токи. Этот способ уменьшает сложность данных по сравнению с 4-D поиском в таблице и, следовательно, приводит к повышению производительности моделирования.
Данные о частной производной 4-D - 4-D поиск по таблице, на основе трех статоров извилистый ток и угол ротора. Предоставляются данные поиска потока для фазы. Эта модель имеет лучшую точность из трех, но также является наиболее дорогостоящей с точки зрения производительности моделирования и требований к памяти.
3D данные о потокосцеплении - 3D поиск по таблице, на основе данных о потокосцеплении. Можно предоставить данные связывания потоков в различных форматах. Блок использует преобразование Park для отображения трех токов обмотки статора на прямые и квадратурные токи. Этот способ уменьшает сложность данных по сравнению с 4-D поиском в таблице и, следовательно, приводит к повышению производительности моделирования.
По умолчанию все варианты блоков реализуют для обмоток статора конфигурацию wye-raw. Однако можно переключиться на конфигурацию с дельта-раной, выбираемую с помощью параметра типа намотки. В конфигурации с дельта-намоткой фаза a соединяется между портами a и b, фаза b - между портами b и c и фаза c - между портами c и a.
Чтобы получить доступ к этим методам параметризации, щелкните правой кнопкой мыши блок в модели, выберите «Simscape» > «Block choices», а затем выберите требуемый вариант блока с тепловыми портами или без них. По умолчанию тепловые порты не отображаются. Дополнительные сведения см. в разделе Тепловые порты.
В этой модели данных 2-D потока предполагается, что поток, связывающий каждую обмотку, нелинейно зависит только от тока в той же самой обмотке плюс угол ротора. На практике это является разумным предположением для многих синхронных двигателей с постоянными магнитами; однако она менее точна для электродвигателей с переключаемым сопротивлением. Учитывая это предположение, потоки в трех обмотках являются:
[
где ia) - связь потока для А-фазной обмотки как функция угла ротора и А-фазного тока. Startr = 0 соответствует роторуd- ось, выровненная с А-фазным направлением положительного магнитного потока. Мс - взаимная индуктивность статор-статор.
Для улучшенной числовой производительности уравнения, осуществленные в блоке на самом деле, работают с частными производными потокосцепления относительно тока, ∂i, и угол ротора/ ∂ θr, а не поток непосредственно. Если пакет КЭМ не экспортирует эти частные производные, их можно определить с помощью сценария MATLAB ®. Пример этого см. в примере модели «Электромагнитный параметр с данными КЭМ» (Solenoid Parameterized with FEM Data) и в поддерживающем ее сценарии MATLAB.
Электрическими уравнениями для блока, определяемыми в терминах частных производных потока, являются:
dibdt) + Rsic
где
va, vb, vc - напряжения, прикладываемые к обмоткам статора A, B и C.
ia, ib, ic - токи статора в каждой из трех обмоток.
Rs - сопротивление каждой из обмоток статора.
Мс - взаимная индуктивность статор-статор.
являются частными производными связи потока относительно тока статора в каждой из трех обмоток.
- частная производная связи потока относительно угла ротора.
Блок может автоматически вычислить матрицу крутящего момента на основе предоставленной информации о потоке. Также можно задать матрицу Вычислить крутящий момент (Calculate torque matrix)? параметр для No и непосредственно определять крутящий момент как функцию тока и угла ротора. Дополнительные сведения см. на странице привязки блока КЭМ-параметризованного поворотного привода.
В этой модели данных 2-D потока предполагается, что поток, связывающий каждую обмотку, нелинейно зависит от всех токов обмотки статора, плюс предполагается, что связь потока постоянного магнита является синусоидальной. Внутренние магнитные PMSM (или IPMSM) обычно хорошо подходят под это предположение. Уравнения:
δm (id, iq)]
idiqLq (id, iq))
где
id и iq являются d-axis и q- осевые токи соответственно.
/ d/и/q/являются d-axis и q- осевые связи потоков соответственно.
β m - связь постоянного магнитного потока.
Ld и Lq являются d-axis и q- индуктивности оси соответственно. Предполагается, что они зависят от d-axis и q- осевые токи.
N - число пар полюсов.
T - электрический крутящий момент.
Работа с четырехмерными данными имеет как стоимость производительности моделирования, так и стоимость памяти. Чтобы уменьшить размер таблицы до трехмерного, 3-D модель данных использует преобразование Park для отображения трех токов на прямые и квадратурные токи:
sin (starte + 2ā3)] [iaibic]
В общем случае преобразование Park отображает прямые, квадратурные и нулевые токи. Однако ток нулевой последовательности обычно мал при нормальных рабочих условиях. Поэтому модель пренебрегает зависимостью членов связи потока от тока нулевой последовательности и определяет связь потока в терминах только прямых и квадратурных токов плюс угол ротора. Уравнение потока для модели 3-D данных:
iq, r − 4λ/( 3N))]
Электрические уравнения для блока также определяются в терминах частных производных потока, аналогично модели 4-D данных. Вы можете вычислить 3D данные о частной производной потокосцепления из 4-D использования данных о потокосцеплении ee_calculateFluxPartialDerivatives.
Поток, связывающий каждую из обмоток, является функцией тока в этой обмотке, токов в двух других обмотках и угла ротора. Для полной точности модель данных 4-D потока предполагает, что связь потока является функцией трех токов и угла ротора, поэтому выполняет четырехмерные табличные поиски. Уравнение потока:
ia, ib/r − 4/( 3N))]
где
а, b, с - флюсовые связи для обмоток статора А, В и С.
ia, ib, ic - токи статора в каждой из трех обмоток.
Λ r - угол поворота ротора. Δ r = 0 соответствует случаю, когда поток постоянного магнита совмещен с потоком обмотки статора А-фазы.
N - число пар полюсов.
Данные о связывании потоков принимают циклическими с Если, например, двигатель имеет шесть пар полюсов, то диапазон для данных равен 0 ≤ Startr ≤ 60 °. Необходимо предоставить данные как при 0, так и при 60 градусах, и поскольку данные являются циклическими, частные производные связи потоков должны быть одинаковыми в этих двух конечных точках.
Уравнение крутящего момента:
ic, startr)
Модель данных 4-D не имеет опции для блока для определения крутящего момента на основе связи потока. Из-за увеличения числовых накладных расходов в 4-D случае лучше предварительно рассчитать крутящий момент всего один раз, а не вычислять его каждый раз при выполнении моделирования.
Для улучшения числовых характеристик уравнения, реализованные в блоке, фактически работают с частными производными связи потока относительно трех токов и угла ротора, а не непосредственно потока. Если пакет КЭМ не экспортирует эти частные производные, их можно определить с помощью ee_calculateFluxPartialDerivatives.
Электрическими уравнениями для блока, определяемыми в терминах частных производных потока, являются:
где
va, vb, vc - напряжения, прикладываемые к обмоткам статора A, B и C.
ia, ib, ic - токи статора в каждой из трех обмоток.
Rs - сопротивление каждой из обмоток статора.
3D варианты данных о потокосцеплении позволяют Вам работать с сырыми данными о потокосцеплении, экспортируемыми от Вашего моторного средства проектирования конечного элемента (FE). Это в отличие от 3-D опций данных частных производных, для которых необходимо определить частные производные. Можно предоставить данные о связях потоков в различных форматах для поддержки различных соглашений об инструментах FE:
Таблица DQ-осей данных о связях потоков или A-фазных связях потоков - Некоторые инструменты поддерживают работу с связями потоков, разделенными на прямые (D) и квадратурные (Q) оси. Преимуществом этого подхода является то, что требуются данные для углов роторов в диапазоне от 0 до 360/N/3 градусов (где N - количество пар полюсов). Другие инструменты работают непосредственно со связями потока фазы A-, B- и C, и для этого можно импортировать только связь потока фазы A, для которой диапазон углов ротора должен быть в диапазоне от 0 до 360/N градусов. Неявное предположение об импорте только данных фазы A состоит в том, что данные фазы B и C являются одинаковыми, за исключением сдвинутых по фазе.
Табуляция с использованием декартовых или полярных координат тока - декартова табуляция подразумевает, что связь потока табулируется в терминах тока по оси D и тока по оси Q (плюс угол ротора). Альтернативно, полярная табуляция включает в себя табулирование связей потока в терминах величины тока, угла опережения тока относительно оси Q и угла ротора. Преимущество полярных координат заключается в том, что они более естественно отражают допустимые рабочие токи, тем самым избегая неиспользуемых табличных точек данных.
Эти соглашения приводят к четырем вариантам параметризации формата данных связи Flux:
D and Q axes flux linkages as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta)
D and Q axes flux linkages as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta)
A-phase flux linkage as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta)
A-phase flux linkage as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta)
Помимо выбора формата данных связи потока, используемого инструментом FE, необходимо выбрать версию преобразования Park, используемого инструментом. Четыре соглашения описаны ниже и соответствуют четырем опциям раскрывающегося меню «Park's convention for tabled data».
Примечание
При просмотре записанных значений для токов по осям D- и Q следует иметь в виду, что для каждой из этих опций формат преобразуется по мере необходимости, так что внутри блока FEM-Parameterized PMSM последовательно используется опция 1.
Это соглашение Парка, используемое внутри Simscape™ Electrical™ моторных и машинных блоков. Все остальные параметры преобразуются в этот формат.
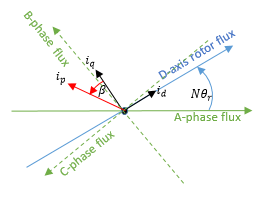
N: число пар полюсов
startr: угол ротора
токи id, iq: D-ось и Q-ось
ip: Величина тока = iq2
β: Текущий угол опережения = id/iq)
Соответствующее преобразование парка
N, r + 2ā3) 121212] [iaibic]
где ia, ib и ic - А-фазный, В-фазный и С-фазный токи соответственно.
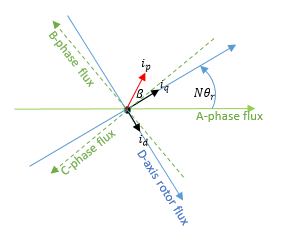
N: число пар полюсов
startr: угол ротора
токи id, iq: D-ось и Q-ось
ip: Величина тока = iq2
β: Текущий угол опережения = id/iq)
Соответствующее преобразование парка
+ 2í63) 121212] [iaibic]
где ia, ib и ic - А-фазный, В-фазный и С-фазный токи соответственно.
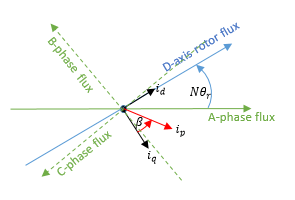
N: число пар полюсов
startr: угол ротора
токи id, iq: D-ось и Q-ось
ip: Величина тока = iq2
β: Текущий угол опережения = id/iq)
Соответствующее преобразование парка
+ 2ā3) 121212] [iaibic]
где ia, ib и ic - А-фазный, В-фазный и С-фазный токи соответственно.
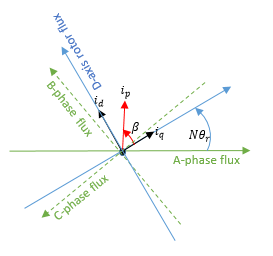
N: число пар полюсов
startr: угол ротора
токи id, iq: D-ось и Q-ось
ip: Величина тока = iq2
β: Текущий угол опережения = id/iq)
Соответствующее преобразование парка
N, r + 2ā3) 121212] [iaibic]
где ia, ib и ic - А-фазный, В-фазный и С-фазный токи соответственно.
Блок FEM-Parameterized PMSM моделирует потери железа в соответствии с выбранными методами параметризации для потока и крутящего момента.
Для 2-D данных частных производных, 3-D данных частных производных и 4-D вариантов данных частных производных с тепловыми портами или без них модель потерь железа основана на работе Меллера [1]. Потери железа делятся на два члена, один из которых представляет основную траекторию намагничивания, а другой - поперечную траекторию острия зуба, которая становится активной во время работы с ослабленным полем.
Термин, представляющий основной путь намагничивания, зависит от индуцированного среднеквадратичного напряжения статора, :
aexk1.5Vmrms1.5
Это доминирующий термин при работе без нагрузки. k - обратная постоянная ЭДС, относящаяся к среднеквадратичным вольтам на Гц. Определяется как Vmrms/f, где f - электрическая частота. Первый член с правой стороны - магнитные гистерезисные потери, второй - вихревые токовые потери и третий - избыточные потери. Три коэффициента, отображаемые на числителях, получаются из значений, которые предоставляются для гистерезиса с разомкнутым контуром, вихревых и избыточных потерь.
Термин, представляющий траекторию поперечной вершины зуба, становится важным, когда установлено поле размагничивания, и может быть определен из теста короткого замыкания на конечно-элементный анализ. Это зависит от среднеквадратичного значения, связанного с потоком наконечника поперечного зуба, *:
bexk1.5Vdrms * 1,5
Три числительных члена получаются из значений, которые вы предоставляете для гистерезиса короткого замыкания, вихревых и избыточных потерь.
Для данных связи 3-D потока с тепловыми портами или без них можно также моделировать потери железа на основе уравнения Штейнмеца. Метод Штейнметца масштабирует различные скорости двигателя или электрические частоты, так что данные о потерях железа требуются только в зависимости от токов двигателя. Если для параметра моделирования потерь железа задано значение Specify open and short circuit loss data (permanent magnet motors only)блок использует метод Штейнметца, но предполагает постоянные коэффициенты и отсутствие зависимости от пикового тока и продвижения по фазе тока. И наоборот, если для параметра Формат данных связи потока (Flux linkage data format) задано значение D and Q axes flux linkages as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta) или A-phase flux linkage as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta) затем блок составил таблицу коэффициентов с вектором величины пикового тока, I и вектором угла опережения тока, параметрами B, так что железные потери задаются:
kJs (Ip, β) f2 + kes (Ip, β) f1.5
где:
f - электрическая частота, в Hz.
khr (Ip, β) - коэффициент потери гистерезиса ротора, k_hr (I, B).
kJr (Ip, β) - коэффициент потери вихревого тока ротора, k_Jr (I, B).
ker (Ip, β) - коэффициент потери избыточного тока ротора, k_er (I, B).
khs (Ip, β) - коэффициент потерь гистерезиса статора, k_hs (I, B).
kJs (Ip, β) - коэффициент потери вихревого тока Статора, k_Js (I, B).
kes (Ip, β) - коэффициент потери избыточного тока статора, k_es (I, B).
Аналогично, если для параметра Формат данных связи потока (Flux linkage data format) задано значение: D and Q axes flux linkages as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta) или A-phase flux linkage as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta), то потери железа задаются:
(iD, iQ) f2 + kes (iD, iQ) f1.5
где:
khr (iD, iQ) - коэффициент потери гистерезиса ротора, k_hr (iD, iQ).
kJr (iD, iQ) - коэффициент потери вихревого тока ротора, k_Jr (iD, iQ).
ker (iD, iQ) - коэффициент потери избыточного тока ротора, k_er (iD, iQ).
khs (iD, iQ) - коэффициент потерь гистерезиса статора, k_hs (iD, iQ).
kJs (iD, iQ) - коэффициент потери вихревого тока Статора, k_Js (iD, iQ).
kes (iD, iQ) - коэффициент потери избыточного тока статора, k_es (iD, iQ).
Блок имеет четыре дополнительных тепловых порта, по одному для каждой из трех обмоток и по одному для ротора. По умолчанию эти порты скрыты. Чтобы открыть тепловые порты, щелкните правой кнопкой мыши блок в модели, выберите команду Simscape > Block choices, а затем выберите требуемый вариант блока с тепловыми портами: 2-D данные частных производных | Show thermal port, 3-D данные частных производных | Show thermal port, 4-D данные частных производных | Show thermal port или 3-D данные связи потоков | Show thermal port. Это действие отображает тепловые порты на значке блока и отображает параметры Температурная зависимость (Temperature Dependence) и Тепловой порт (Thermal Port). Эти параметры описаны далее на этой справочной странице.
Используйте тепловые порты для моделирования влияния сопротивления меди и потерь железа, которые преобразуют электроэнергию в тепло. Дополнительные сведения об использовании тепловых портов в блоках привода см. в разделе Моделирование тепловых эффектов во вращательных и поступательных приводах.
Этот блок имеет следующие ограничения:
Для модели 2-D данных взаимная индуктивность статор-статор, определяемая взаимной индуктивностью статора, значением параметра Ms, является постоянной при моделировании и не изменяется с углом ротора. Это означает, что блок подходит для моделирования большинства электродвигателей постоянного тока PMSM и без щеток, но не переключаемых электродвигателей сопротивления.
Модели данных 3-D и 4-D принимают симметрию, так что зависимость связи потока от токов и угла ротора для обмоток B и C может быть определена из зависимости для обмотки A.
Для модели данных 4-D при фиксации значений независимых параметров (трех токов и углов ротора) учитывайте требования к памяти. Опция линейной интерполяции использует меньше памяти, но опция плавной интерполяции более точна для заданного интервала независимых параметров.
Модель потерь железа предполагает синусоидальные токи.
[1] Меллер, П. Х., Р. Вробель и Д. Холлидей. «Вычислительно эффективная модель потерь железа для бесщеточных машин переменного тока, которая обеспечивает номинальный поток и ослабленную работу в полевых условиях». Конференция по электрическим машинам и приводам IEEE. Май 2009 года.
ee_calculateFluxPartialDerivatives | КЭМ-параметризованный линейный исполнительный механизм | КЭМ - параметризованный поворотный привод