Реализовать преобразование abc в dq0
Simscape / Электрический / Контроль / Математические Преобразования
Блок Park Transform преобразует компоненты временной области трехфазной системы в опорном кадре abc в прямые, квадратурные и нулевые компоненты во вращающемся опорном кадре. Блок может сохранять активные и реактивные мощности с мощностями системы в опорном кадре abc, реализуя инвариантную версию преобразования Парка. Для сбалансированной системы нулевая составляющая равна нулю.
Блок можно настроить для выравнивания оси a трехфазной системы по оси d- или q вращающейся опорной рамки в момент времени t = 0. На чертежах показано направление магнитных осей обмоток статора в abc-системе координат и вращающейся dq0-системе координат, где:
Ось a и ось q первоначально выровнены.
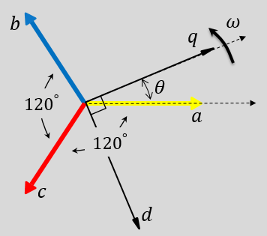
Ось a и ось d первоначально выровнены.
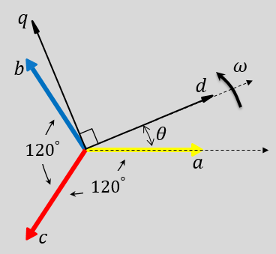
В обоих случаях угол
λ - угол между осями a и q для выравнивания по оси q или угол между осями a и d для выравнивания по оси d.
λ - скорость вращения опорного кадра d-q.
t - время (в с) от начальной юстировки.
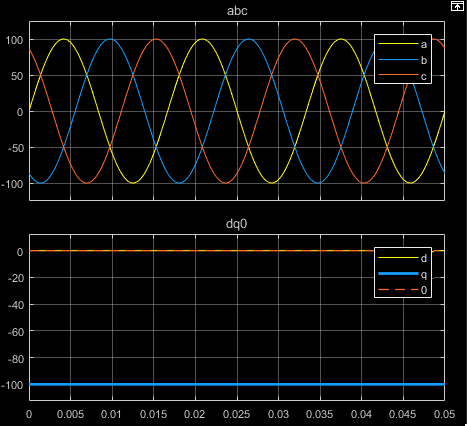
На рисунках показаны временные характеристики отдельных компонентов эквивалентных сбалансированных abc и dq0 для:
Выравнивание а-фазового вектора по оси q
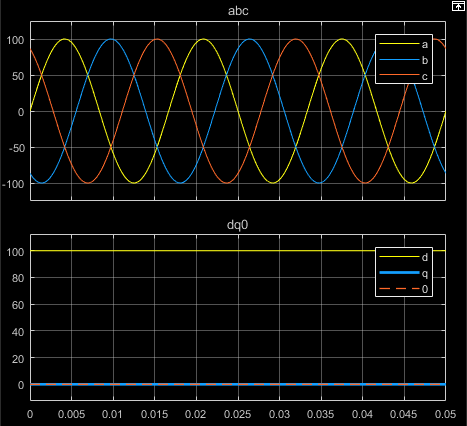
Выравнивание фазового вектора по оси d
Блок Park Transform реализует преобразование для выравнивания от фазы к оси q как
(start+ + 2ā3) 121212] [abc],
где:
a, b и c - компоненты трехфазной системы в опорном кадре abc.
d и q - компоненты двухосной системы в вращающейся опорной раме.
0 - нулевая составляющая двухосной системы в стационарной системе координат.
Для инвариантного по мощности выравнивания от фазы к оси q блок реализует преобразование, используя следующее уравнение:
(start+ 2ā3) 121212] [abc].
Для выравнивания a-фазы по d-оси блок реализует преобразование, используя следующее уравнение:
sin (start+ 2ā3) 121212] [abc].
Блок реализует инвариантное выравнивание a-фазы по d-оси как
sin (start+ 2ā3) 121212] [abc].
[1] Краузе, П., О. Васынчук, С. Д. Судхофф и С. Пекарек. Анализ электрических машин и приводных систем. Piscatawy, NJ: Wiley-IEEE Press, 2013.