Шестифазная синхронная машина
Simscape/Электрическая/Электромеханическая/Синхронная
Блок синхронной машины (шестифазной) моделирует шестифазную синхронную машину, также известную как двухзвездочная машина.
Шестифазная синхронная машина имеет две группы обмоток статора: группу ABC и группу XYZ. Эти две группы имеют сдвиг фазы на 30 градусов.
Эквивалентные схемы шестифазной синхронной машины для прямой оси, квадратурной оси и двух нулевых последовательностей:
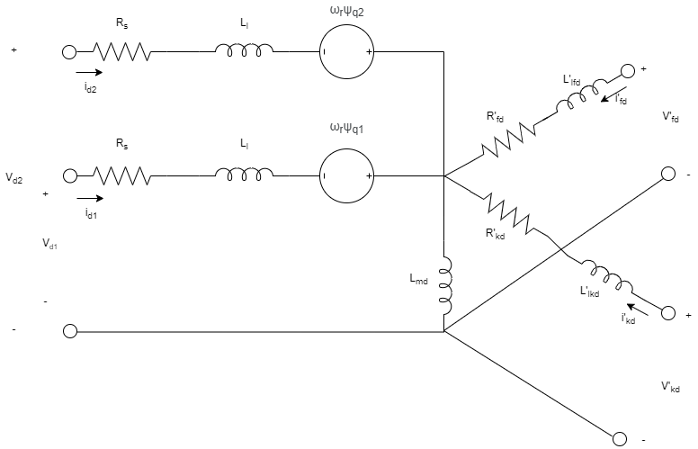
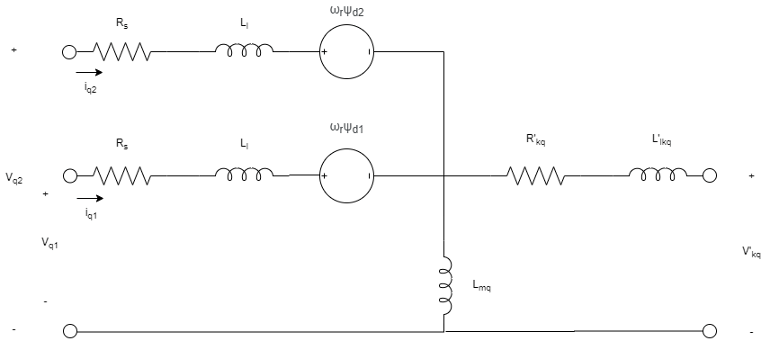
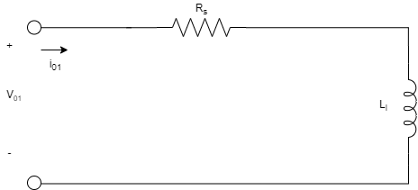
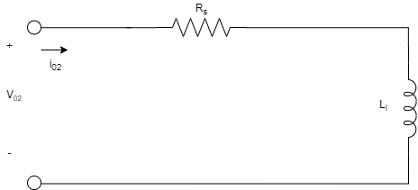
Уравнения синхронной машины выражены относительно синхронно вращающейся системы отсчета, определяемой:
_ offset,
где:
starte - электрический угол ротора.
N - число пар полюсов.
startr - механический угол ротора.
x_rotor_offset является 0 если вы определяете электрический угол ротора относительно оси d, или -pi/2 при определении электрического угла ротора относительно оси q.
Два преобразования Park отображают уравнения синхронной машины на вращающуюся опорную рамку относительно электрического угла. Преобразование Park для первой группы обмоток статора, группы ABC, определяется следующим образом:
sin (starte + 2ā3) 121212].
Преобразование Парка для второй группы обмоток статора, группы XYZ, определяется следующим образом:
− 5security6) sin (starte + security2) 121212].
Преобразования Park используются для определения уравнений синхронной машины на единицу измерения.
Уравнения напряжения статора для группы ABC определяются:
где:
vd1, vq1 и v01 - напряжения статора ABC d-оси, q-оси и нулевой последовательности, определяемые:
vavbvc].
va, vb и vc - напряжения статора ABC, измеряемые от порта _ ABC к нейтральному порту n1.
λ base - базовая электрическая скорость на единицу.
Для группы ABC связи статора по d-оси, q-оси и нулевым последовательностям.
startr - частота вращения ротора на единицу.
Rs - сопротивление статора.
id1, iq1 и i01 - токи статора ABC d-оси, q-оси и нулевой последовательности, определяемые:
iAiBiC].
ia, ib и ic - токи статора ABC, протекающие от порта _ ABC к порту n1.
Уравнения напряжения статора для группы XYZ определяются:
где:
vd2, vq2 и v02 являются напряжениями статора XYZ d-оси, q-оси и нулевой последовательности, определяемыми:
vxvyvz].
vx, vy и vz - напряжения статора XYZ, измеренные от порта ~ XYZ до нейтрального порта n2.
Для группы XYZ связи статора по d-оси, q-оси и нулевым последовательностям представляют собой связи потока статора.
id2, iq2 и i02 - токи статора XYZ d-оси, q-оси и нулевой последовательности, определяемые:
iXiYiZ].
ix, iy и iz - токи статора XYZ, протекающие от порта ~ XYZ к порту n2.
Уравнения напряжения ротора определяются:
1ü based( кддт) = 0
1ü based, "kqdt = 0
где:
v 'fd - напряжение обмотки возбуждения, относящееся к стороне статора.
v 'kd и v' kq - напряжения обмотки демпфера по dq-осям, относящиеся к стороне статора. Все они равны 0.
в качестве магнитных потоков, связывающих цепь возбуждения, обмотку демпфера d-оси и обмотку демпфера q-оси.
R 'fd, R' kd и R 'kq - сопротивления цепи возбуждения ротора, обмотки демпфера d-оси и обмотки демпфера q-оси.
i 'fd, i' kd и i 'kq - токи обмотки демпфера по полю и dq-осям, относящиеся к стороне статора.
Уравнения связи статорного потока определяются:
id1+id2+i′fd+i′kd)
iq1+iq2+i′kq)
id1+id2+i′fd+i′kd)
iq1+iq2+i′kq)
где:
L1 - индуктивность утечки статора.
Lmd и Lmq - взаимные индуктивности d-оси статора и q-оси.
Уравнения связи потока ротора определяются:
id1+id2+i′fd+i′kd)
id1+id2+i′fd+i′kd)
iq1+iq2+i′kq)
где:
L 'lfd - индуктивность обмотки поля ротора.
L 'lkd - индуктивность обмотки демпфера ротора d-оси.
L '1kg - индуктивность обмотки заслонки q-оси ротора.
Крутящий момент ротора определяется:
Параметры «Переменные» позволяют задать приоритет и начальные целевые значения для переменных блока перед моделированием. Дополнительные сведения см. в разделе Установка приоритета и начальной цели для переменных блока.
Для этого блока параметры «Переменные» отображаются только в том случае, если в параметрах «Начальные условия» для параметра «Инициализация» установлено значение Set targets for rotor angle and Park's transform variables.
[1] Киферндорф, Ф., Бурзановская, Х., Канерва С., Сарио П. «Моделирование гармоник на основе ротора в двухзвездочных, намотанных, синхронных машинах». 2008 18-я Международная конференция по электрическим машинам: Виламура, 1-6.
[2] Burzanowska, H., Sario P, Stulz C., Joerg P. «Резервный привод с прямым управлением крутящим моментом (DTC) и двухзвездочный синхронный автомат, моделирование и проверки». 2007 Европейская конференция по силовой электронике и приложениям: Ольборг, 1-10.
Цепь поля синхронной машины | Измерение синхронной машины | Синхронная машина модели 1.0 | Синхронная машина модель 2.1 | Синхронная машина с круглым ротором | Явный полюс синхронной машины