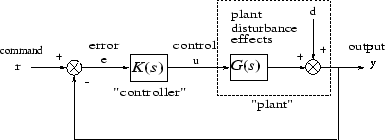
Рассмотрим систему управления с многопараметрической обратной связью, показанную на следующем рисунке. Чтобы количественно определить многовариантные пределы стабильности и производительность таких систем, можно использовать сингулярные значения матриц функций передачи с обратной связью от r до каждого из трех выходов e, u и y, т.е..
defL (s) (I + L (s)) − 1 = I − S (s)
где L (s) является матрицей функции передачи цикла
| K (s). | (1) |
Блок-схема системы управления с многопараметрической обратной связью
Две матрицы S (s) и T (s) известны как функция чувствительности и функция комплементарной чувствительности соответственно. Матрица R (ы) не имеет общего имени. Сингулярные графики Боде каждой из трех матриц S (s), R (s) и T (s) передаточных функций играют важную роль в надежной конструкции системы управления с несколькими переменными. Сингулярные значения матрицы L (s) функции передачи цикла важны, поскольку L (s) определяет матрицы S (s) и T (s).
Сингулярные значения S (jλ) определяют затухание возмущения, поскольку S (s) фактически является функцией передачи с обратной связью от возмущения d к выходному сигналу установки y - см. Блок-схему системы управления с многопараметрической обратной связью. Таким образом, спецификация характеристик ослабления возмущений может быть записана как
| (jλ) | | (2) |
где jλ) | - требуемый коэффициент затухания возмущений. W1 (jλ) | зависеть от частоты, можно задать различные коэффициенты затухания для каждой частоты.
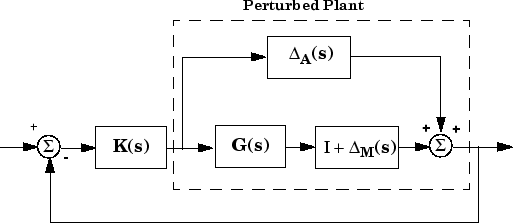
Сингулярные графики Боде R (s) и T (s) используются для измерения пределов устойчивости многовариантных схем обратной связи перед аддитивными возмущениями ΔA растений и мультипликативными возмущениями ΔM растений соответственно. См. следующий рисунок.
Рассмотрим, как сингулярный график Боде комплементарной чувствительности T (s) определяет запас устойчивости для мультипликативных возмущений ΔM. Предел мультипликативной устойчивости по определению является «размером» наименьшего стабильного ΔM (s), который дестабилизирует систему на приведенном ниже рисунке, когда ΔA = 0.
Аддитивная/мультипликативная неопределенность
Принимая в качестве определения «размера» ΔM (jλ)) (ΔM), имеется следующая полезная характеристика «мультипликативной» устойчивости:
Мультипликативная надежность:
Размер наименьшей дестабилизирующей мультипликативной неопределенности ΔM (s) равен:
T (jλ)).
Чем меньше (jλ)), тем больше будет размер наименьшего дестабилизирующего мультипликативного возмущения, и, следовательно, тем больше будет запас устойчивости.
Аналогичный результат доступен для связи запаса устойчивости в условиях аддитивных растительных возмущений ΔA (s) с R (s), если (jλ)) за определение «размера» ΔA (jλ) на частоте λ.
Аддитивная устойчивость:
Размер наименьшей дестабилизирующей аддитивной неопределенности ΔA составляет:
(jλ)).
Как следствие теорем о надежности 1 и 2, обычно определяют пределы устойчивости систем управления посредством сингулярных неравенств значений, таких как
| (jλ) | | (3) |
| (jλ) | | (4) |
где | W2 (jλ) | и | W3 (jλ) | - соответствующие размеры наибольших ожидаемых аддитивных и мультипликативных возмущений растений.
Обычной практикой является сведение последствий всей неопределенности растений в единое фиктивное мультипликативное возмущение ΔM, чтобы можно было записать требования к конструкции управления.
|W3−1 (jω) |
как показано в спецификациях сингулярного значения для L, S и T.
Интересно отметить, что в верхней половине рисунка (выше линии 0 дБ),
(jλ))
в нижней половине Спецификации сингулярного значения для L, S и T (ниже линии 0 дБ),
(jλ)).
Это является результатом того, что
−1≈L (s) − 1
если ) ≫1, и
) −1≈L (s)
если ) ≪1.
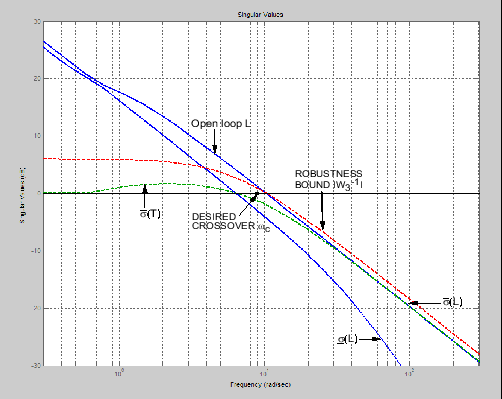
Спецификации сингулярных значений для L, S и T
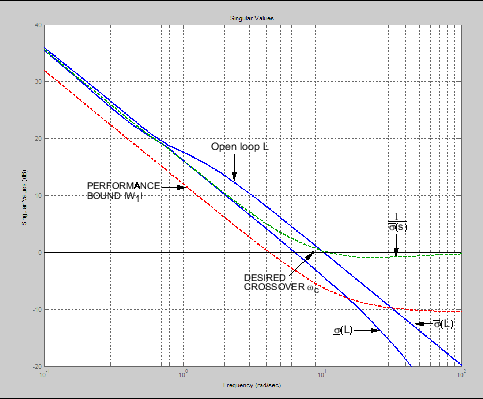
Таким образом, нередки случаи, когда спецификации по ослаблению возмущений и пределу мультипликативной устойчивости выражаются непосредственно в терминах запрещенных областей для графиков Боде, таких как
Для тех, кому более удобны классические однокольцевые концепции, существуют важные связи между предугадываемыми () полями мультипликативной устойчивости
1 + L (jλ) |
именно такую величину вы получаете из М-кругов диаграммы Николса. Таким образом, T‖∞ представляет собой многоточечное обобщение резонансной пиковой величины с замкнутым контуром, которое, как признают специалисты по классическому управлению, тесно связано с коэффициентом демпфирования доминирующих полюсов с замкнутым контуром. Также, оказывается, что можно соотнести T‖∞S‖∞ с классическим запасом GM усиления и запасом λ M фазы в каждом контуре обратной связи многовариантной системы обратной связи Блок-схемы многовариантной системы управления обратной связью по формулам:
12‖T‖∞).
(См. раздел [6].) Эти формулы действительны при условии, что S‖∞ и T‖∞ больше 1, как обычно. Поля применяются, даже когда возмущения усиления или возмущения фазы возникают одновременно в нескольких каналах обратной связи.
Нормы бесконечности S и T также дают допуски снижения коэффициента усиления. Допуск уменьшения усиления gm определяется как минимальная величина, на которую коэффициенты усиления в каждом контуре должны быть уменьшены для дестабилизации системы. Верхние границы на gm следующие:
Команда loopsyn позволяет разработать стабилизирующий контроллер обратной связи, чтобы оптимально формировать частотную характеристику разомкнутого контура системы управления обратной связью MIMO так, чтобы максимально соответствовать требуемой форме контура Gd. Основной синтаксис loopsyn команда синтеза контроллера формирования петель:
K = loopsyn(G,Gd)
Здесь G - матрица передаточной функции LTI модели установки MIMO, Gd - целевая требуемая форма цикла для функции передачи цикла L=G*K, и K является оптимальным контроллером формирования петель. Контроллер LTI K имеет свойство, которое формирует цикл L=G*K чтобы он соответствовал частотной характеристике Gd как можно ближе при условии, что компенсатор должен стабилизировать модель установки G.