Чтобы увидеть, как loopsyn на практике команда работает над поиском компромиссов в отношении надежности и производительности, снова рассмотрим модель самолета NASA HiMAT, взятую из работы Сафонова, Лауба и Хартманна [8]. Продольная динамика самолета HiMAT, обрезанного на 25000 футов и 0,9 Маха, неустойчива и имеет два режима фугоида правой полуплоскости. Линейная модель имеет реализацию состояния-пространства G (s ) = C ( Is - A) -1B с шестью состояниями, с первыми четырьмя состояниями, представляющими угол атаки (α) и угол ориентации (
ag = [
-2.2567e-02 -3.6617e+01 -1.8897e+01 -3.2090e+01 3.2509e+00 -7.6257e-01;
9.2572e-05 -1.8997e+00 9.8312e-01 -7.2562e-04 -1.7080e-01 -4.9652e-03;
1.2338e-02 1.1720e+01 -2.6316e+00 8.7582e-04 -3.1604e+01 2.2396e+01;
0 0 1.0000e+00 0 0 0;
0 0 0 0 -3.0000e+01 0;
0 0 0 0 0 -3.0000e+01];
bg = [0 0;
0 0;
0 0;
0 0;
30 0;
0 30];
cg = [0 1 0 0 0 0;
0 0 0 1 0 0];
dg = [0 0;
0 0];
G = ss(ag,bg,cg,dg);Управляющими переменными являются исполнительные механизмы (δe и δc). Выходными переменными являются угол атаки (α) и угол ориентации (start).
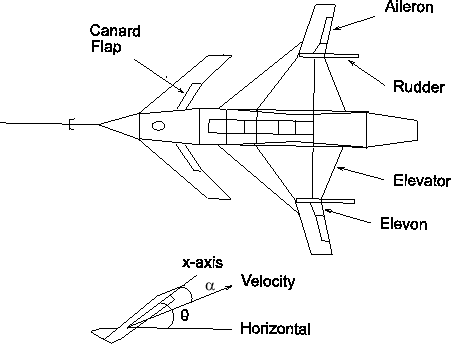
Конфигурация самолета и геометрия вертикальной плоскости
Эта модель хороша на частотах ниже 100 рад/с с менее чем 30% вариацией между истинным самолетом и моделью в этом диапазоне частот. Однако, как отмечено в [8], он не улавливает надежно очень высокочастотное поведение, поскольку он был получен, рассматривая летательный аппарат как жесткое тело и пренебрегая слегка затухающими режимами изгиба фюзеляжа, которые происходят где-то от 100 до 300 рад/с. Эти немодулированные режимы изгиба могут привести к отклонению в 20 дБ (т.е. 1000%) между частотной характеристикой модели и фактическим самолетом для частоты λ > 100 рад/с. Другие эффекты, такие как задержки времени исполнительного механизма управления и проскальзывание топлива, также способствуют неточности модели на еще более высоких частотах, но доминирующими немодулированными эффектами являются режимы изгиба фюзеляжа. Эти немодулированные режимы изгиба можно рассматривать как мультипликативную неопределённость размера 20 дБ, и проектировать свой контроллер с помощью шлейфа, убедившись, что коэффициент усиления контура составляет менее -20 дБ при и за его пределами, на частоте λ > 100 рад/с.
Расчетные спецификации с единственным значением:
Технические требования к надежности: наклон скатывания -20 дБ/декада и коэффициент усиления контура -20 дБ при скорости 100 рад/с
Спецификация производительности: максимально минимизировать функцию чувствительности.
Обе характеристики можно адаптировать, приняв за желаемую форму петли
Gd (s) = 8/с
s = zpk('s'); % Laplace variable s Gd = 8/s; % desired loop shape % Compute the optimal loop shaping controller K [K,CL,GAM] = loopsyn(G,Gd); % Compute the loop L, sensitivity S and complementary sensitivity T: L = G*K; I = eye(size(L)); S = feedback(I,L); % S=inv(I+L); T = I-S; % Plot the results: % step response plots step(T);title('\alpha and \theta command step responses');

% frequency response plots figure; sigma(L,'r--',Gd,'k-.',Gd/GAM,'k:',Gd*GAM,'k:',{.1,100}) legend('\sigma(L) loopshape',... '\sigma(Gd) desired loop',... '\sigma(Gd) \pm GAM, dB');

figure; sigma(T,I+L,'r--',{.1,100}) legend('\sigma(T) robustness','1/\sigma(S) performance')

Число ± GAM, дБ (т.е. 20log10 (GAM)) указывает точность, с которой loopsyn проект управления соответствует целевому требуемому контуру:
(λ > λ c).