Аппроксимация минимальной степени (MDA) Hankel без балансировки
GRED = hankelmr(G) GRED = hankelmr(G,order) [GRED,redinfo] = hankelmr(G,key1,value1,...) [GRED,redinfo] = hankelmr(G,order,key1,value1,...)
hankelmr возвращает модель сокращенного заказа GRED из G и массив структуры redinfo содержит границу ошибки уменьшенной модели и сингулярные значения Ханкеля исходной системы.
Граница ошибки вычисляется на основе сингулярных значений Ханкеля G. Для стабильной системы сингулярные значения Hankel указывают соответствующую энергию состояния системы. Следовательно, уменьшенный порядок может быть непосредственно определен путем исследования системы Hankel SV's,
Только с одним входным аргументом G, функция покажет график сингулярных значений Ханкеля исходной модели и предложит уменьшить номер заказа модели.
Этот метод гарантирует привязку ошибки к бесконечной норме аддитивной ошибки ∥G-GRED∥ ∞ для хорошо кондиционированной модели уменьшил проблемы [1]:
Примечание
Похоже, что этот метод похож на процедуры снижения аддитивной модели balancmr и schurmr, но на самом деле она может производить более надежную модель уменьшенного порядка, когда желаемая модель уменьшенного порядка имеет почти управляемые и/или наблюдаемые состояния (имеет сингулярные значения Ханкеля, близкие к точности машины). hankelmr затем выберет оптимальную уменьшенную систему, чтобы удовлетворить критерию ограничения ошибок, независимо от порядка, который можно наивно выбрать в начале.
В этой таблице описаны входные аргументы для hankelmr.
Аргумент | Описание |
|---|---|
G | Модель LTI должна быть уменьшена (без каких-либо других входных данных построят график ее сингулярных значений Ханкеля и предложат уменьшить порядок) |
ORDER | (Необязательно) целое число для требуемого порядка уменьшенной модели или, необязательно, вектор, упакованный с требуемыми заказами для пакетных прогонов |
Пакетное выполнение серии различных моделей сокращенного заказа может быть создано путем указания order = x:y, or a vector of integers. По умолчанию вся антистабильная часть системы сохраняется, поскольку с точки зрения стабильности управления избавление от нестабильного состояния (состояний) опасно для моделирования системы.
'MaxError' может быть указан таким же образом, как альтернатива для 'ORDER'. В этом случае уменьшенный порядок будет определен, когда сумма хвостов Hankel sv достигнет 'MaxError'.
Аргумент | Стоимость | Описание |
|---|---|---|
'MaxError' | Действительное число или вектор различных ошибок | Сокращение для достижения H∞ ошибки. При наличии, |
'Weights' |
| Оптимальный массив ячеек 1x2 с весами LTI |
'Display' |
| Отображение сингулярных графиков Hankel (по умолчанию |
'Order' | Целое число, вектор или массив ячеек | Порядок уменьшенной модели. Используйте, только если не указан в качестве второго аргумента. |
Веса на входе и/или выходе исходной модели могут заставить алгоритм уменьшения модели сосредоточиться на некотором частотном диапазоне интересов. Но веса должны быть стабильными, минимальными по фазе и обратимыми.
В этой таблице описываются выходные аргументы.
Аргумент | Описание |
|---|---|
GRED | Модель сокращенного заказа LTI. Становится многомерным массивом, когда вход является последовательным массивом различных порядков модели. |
REDINFO | Массив STRUCT с 4 полями:
|
G может быть стабильным или нестабильным, непрерывным или дискретным.
Примечание
Если size(GRED) не равен указанному порядку. Оптимальный алгоритм Hankel MDA выбрал наилучшую минимальную степень приближения, которую он может найти в пределах допустимой точности машины.
Учитывая непрерывную или дискретную, стабильную или нестабильную систему, G, следующие команды могут получить набор моделей уменьшенного порядка на основе выбранных вами вариантов:
rng(1234,'twister'); G = rss(30,5,4); [g1, redinfo1] = hankelmr(G); % display Hankel SV plot % and prompt for order (try 15:20) [g2, redinfo2] = hankelmr(G,20); [g3, redinfo3] = hankelmr(G,[10:2:18]); [g4, redinfo4] = hankelmr(G,'MaxError',[0.01, 0.05]); for i = 1:4 figure(i); eval(['sigma(G,g' num2str(i) ');']); end
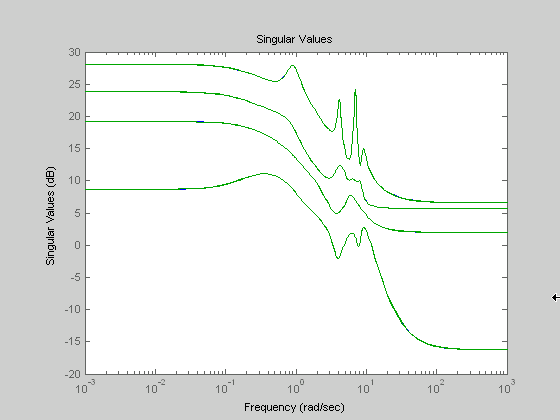
График сингулярного значения Bode G (30 состояний, 5 выходов, 4 входа) показывает график сингулярного значения Bode случайной системы G с 20 состояниями, 5 выходными и 4 входами. Система ошибок между G и его Zeroth порядка Hankel MDA имеет бесконечность норму, равную функции всех проходов, как показано в All-Pass Error System между G и Zeroth Order G Anticausal.
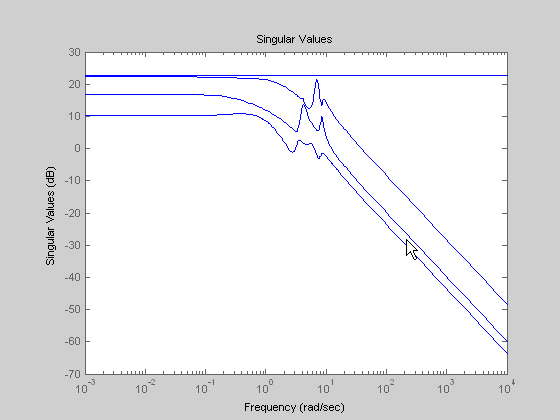
График Zeroth порядка Hankel MDA и его система ошибок sigma получаются с помощью команд
[g0,redinfo0] = hankelmr(G,0); sigma(G-redinfo0.Ganticausal)
Это интересное всепроходное свойство уникально в сокращении модели Hankel MDA.
График модели сингулярного значения G (30 состояний, 5 выходов, 4 входа)
Всепроходная система ошибок между G и нулевым порядком G Anticausal
Учитывая состояние-пространство (A, B, C, D) системы и k, желаемый уменьшенный порядок, следующие этапы будут производить преобразование подобия для усечения исходной системы состояния-пространства до модели с уменьшенным k-м порядком.
Найдите грамматики управляемости и наблюдаемости P и Q.
Сформировать дескриптор
α2I
где , и состояние дескриптора-пробел
Возьмите SVD дескриптора E и разбейте результат на k-ый порядок формы усечения
[ΣE0000] [VE1TVE2T]
Примените преобразование к описательной системе state-space выше
Сформируйте эквивалентную модель состояния-пространства.
C1−C2A22†A21D1−C2A22†B2]
Последний k-ый порядок Hankel MDA является стабильной частью вышеуказанной реализации состояния-пространства. Его антикаузальная часть хранится в redinfo.Ganticausal.
Доказательство алгоритма Hankel MDA можно найти в [2]. Система ошибок между исходной системой G и G0 Hankel MDA нулевого порядка является полной функцией [1].
[1] Перчаточник, К., «Все оптимальное приближение нормы Ганкеля линейных многовариантных систем и их -ошибочные границы L», интервал. J. Control, том 39, № 6, стр. 1145-1193, 1984.
[2] Сафонов, М.Г., Р.Я. Чянг и Д.Ж.Н. Limebeer, «Оптимальное сокращение модели Hankel для неминалимальных систем», IEEE Trans. on Automat. Контр., том 35, № 4, апрель 1990, стр. 496-502.