Вычислить L2 норму системы непрерывного времени в обратной связи с дискретной системой времени
[gaml,gamu] = sdhinfnorm(sdsys,k) [gaml,gamu] = sdhinfnorm(sdsys,k,delay) [gaml,gamu] = sdhinfnorm(sdsys,k,delay,tol)
[gaml,gamu] = sdhinfnorm(sdsys,k) вычисляет индуцированную L2 норму установки LTI непрерывного времени, sdsys, в обратной связи с дискретным контроллером времени, k, подключенный через идеальный пробоотборник и удержание нулевого порядка (см. рисунок ниже). sdsys должны быть строго правильными, так что постоянный коэффициент усиления обратной связи должен быть равен нулю. Выходы, gamu и gaml, являются верхней и нижней границами на индуцированной норме L2 системы с замкнутым контуром дискретизированных данных.
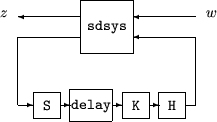
[gaml,gamu] = sdhinfnorm(sdsys,k,h,delay) включает входной аргумент delay. delay - неотрицательное целое число, связанное с количеством вычислительных задержек контроллера. Значение задержки по умолчанию равно 0.
[gaml,gamu] = sdhinfnorm(sdsys,k,h,delay,tol) включает входной аргумент, tol, которая определяет разницу между верхней и нижней границами при завершении поиска. Значение по умолчанию tol составляет 0,001.
Рассмотрим функцию передачи с разомкнутым контуром и непрерывным временем p = 30/s(s+30) и контроллер непрерывного времени k = 4/(s+4). Замкнутая система непрерывного времени имеет пиковую величину на частоте 1.
p = ss(tf(30,[1 30])*tf([1],[1 0]));
k = ss(tf(4,[1 4]));
cl = feedback(p,k);
norm(cl,'inf')
ans =
1
Первоначально контроллер должен быть реализован с частотой дискретизации 1,5 Гц. Норма выборки данных замкнутой системы с дискретным контроллером времени равна 1,0.
kd = c2d(k,0.75,'zoh');
[gu,gl] = sdhinfnorm([1; 1]*p*[1 1],-kd);
[gu gl]
ans =
3.7908 3.7929
Из-за большой разницы в норме между системой с замкнутым контуром непрерывного времени и данных выборки частота дискретизации контроллера увеличивается с 1,5 Гц до 5 Гц. Норма выборки данных новой системы с замкнутым контуром составляет 3,79.
kd = c2d(k,0.2,'zoh');
[gu,gl] = sdhinfnorm([1; 1]*p*[1 1],-kd);
[gu gl]
ans =
1.0044 1.0049
sdhinfnorm использует вариации формул, описанных в документе Бамие и Пирсона, для получения эквивалентной дискретно-временной системы. (Эти изменения делаются для улучшения численного кондиционирования алгоритмов.) Предварительным шагом является определение того, меньше ли норма системы непрерывного времени за один период выборки без контроля, чем заданное значение. Это требует поиска и в вычислительном отношении является относительно дорогостоящим шагом.
Bamieh, B.A., и J.B. Pearson, «Общие рамки линейных периодических систем с применением к выборочному контролю данных», IEEE Transactions on Automatic Control, Vol. AC-37, 1992, pp. 418-435.