Вы можете использовать musyn команда для проектирования надежного контроллера для неопределенной установки, как описано в документе Проектирование надежного контроллера с использованием синтеза Mu. Алгоритм, используемый musyn - итеративный процесс, называемый D-K итерацией. В этом процессе функция:
Использует синтез H∞ для поиска контроллера, который минимизирует коэффициент усиления номинальной системы по замкнутому контуру.
Выполняет анализ надежности для оценки надежной H∞ производительности системы с замкнутым контуром. Эта величина выражается как масштабированная H∞ норма, включающая динамические масштабирования, называемые D и G масштабированием (шаг D).
Поиск нового контроллера для минимизации масштабированной нормы H∞, полученной на шаге 2 (шаг K).
Повторяет шаги 2 и 3 до тех пор, пока надежная производительность не перестанет улучшаться.
И шаг D, и шаг K являются математически интенсивными вычислениями. Ниже приведены подробности алгоритма.
На шаге D musyn вычисляет верхнее граничное H∞ производительности для текущего контроллера К. Шаг D начинается с надежного анализа производительности для неопределенной системы с замкнутым контуром T = LFT (P, K), как показано на следующей диаграмме.
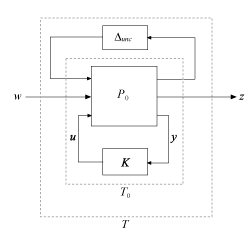
Введение блока Δperf рабочих характеристик преобразует анализ надежности-производительности Т в анализ надежности-стабильности контура обратной связи на следующей диаграмме.
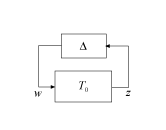
Здесь Δ является дополненной структурой неопределенности
).
musyn вычисляет, что является верхней границей производительности надежного H∞. Для этого musyn выбирает частотную сетку {start1,..., startN}. Только для Т со сложной неопределенностью ,musyn вычисляет на каждой частоте
1 ‖.
Частотно-зависимые матрицы D, которые коммутируются с Δ, называются D масштабами. является наибольшим результатом по всем частотам в сетке,
vet i.
При использовании musyn, можно получить доступ к результатам шага D.
Дефолт musyn на дисплее для каждой итерации в Peak MU столбец.
musyn возвращает каждой итерации в PeakMU области info выходной аргумент.
musyn возвращает Di в DG области info выходной аргумент.
Для визуализации частотной зависимости Di установите 'Display' вариант musynOptions кому 'full'.
Для получения дополнительной информации о вычислениях и интерпретациях, приведенных в Надежный показатель производительности для синтеза Mu».
musyn соответствует рациональной функции D (s) последовательности масштабирования {Di}. Подгонка дает количество мкФ, называемое масштабированной производительностью H∞,
D−1‖∞.
Поскольку аппроксимация не точна, мкФ обычно несколько больше .
Получить доступ к результатам посадки можно несколькими способами.
Дефолт musyn отображает мкФ для каждой итерации в DG Fit столбец.
musyn возвращает мкФ для каждой итерации в PeakMUFit области info выходной аргумент.
musyn возвращает функции фитинга в dr и dc поля info выходной аргумент.
Чтобы визуализировать частотную зависимость функций фитинга, установите 'Display' вариант musynOptions кому 'full'.
T0 зависит от выбора контроллера K соотношением T0 = LFT (P0, K). Поэтому минимизация мкФ по отношению к К является масштабированной проблемой синтеза H∞. Таким образом, на этапе Кmusyn использование hinfsyn или hinfstruct вычислить контроллер К *, который минимизирует мкФ. Минимизированное количество является масштабированной нормой H∞. Чтобы алгоритм достиг прогресса, новый контроллер должен улучшить надежную производительность, полученную на этапе D :
D−1‖∞<μ¯.
В противном случае прогресс недостаточен для компенсации ошибок подгонки. Таким образом musyn завершает процесс итерации D-K, когда K * не улучшает надежную производительность в пределах допуска, заданного 'TolPerf' вариант musynOptions.
Получить доступ к результатам шага K можно несколькими способами.
Дефолт musyn показывает масштабированную норму H∞ для каждой итерации в K Step столбец.
musyn возвращает новый контроллер в K из info выходной аргумент и соответствующая масштабированная норма H∞ для каждой итерации в gamma поле.
Когда система имеет как реальную, так и сложную неопределенность и вы устанавливаете 'MixedMU' вариант musynOptions кому 'on', musyn использует дополнительное G-масштабирование, чтобы улучшить вычисление Алгоритм в этом случае называется смешанным синтезом .
Для смешанной неопределенности, musyn вычисляет i и масштабирования Dr (starti), Dc (starti) и Gcr (starti) таким образом, что
starti)) (T0 (jü i) I) ≤0
на каждой частоте в сетке.
musyn подгоняет данные масштабирования D и G путем построения рациональной функции
00dc (s))
такой, что
dr (s), dc (s) и (s) являются стабильными со стабильными обратными.
dr (s) и dc (s) аппроксимируют квадратные корни диагональных элементов Dr (
F приблизительно удовлетворяет
, J = (Ir00 − Ic).
Наконец, масштабированная производительность H∞ определяется как
∞,
где s) - преобразованная система,
s) T0 (s) dc (s)).
Для точного аппроксимации D и G, = Поэтому в μF≥μ¯.
Поскольку преобразованная система все еще является линейной дробной функцией контроллера K, этап K для случая со смешанной мкМ продолжается вычислением контроллера K *, который T¯‖∞.
При использовании musyn, вы можете получить доступ к D и G масштабам несколькими способами.
musyn возвращает данные масштабирования D и G в DG области info выходной аргумент.
musyn возвращает функции фитинга в dr, dc, и PSI поля info выходной аргумент.
Чтобы визуализировать частотную зависимость данных масштабирования и функций аппроксимации, установите 'Display' вариант musynOptions кому 'full'.
musyn | musynOptions | musynperf