Цифровые фильтры с импульсной характеристикой конечной длительности (все-нулевые или КИХ-фильтры) имеют как преимущества, так и недостатки по сравнению с фильтрами импульсной характеристики бесконечной длительности (БИХ).
Фильтры FIR имеют следующие основные преимущества:
Основным недостатком КИХ-фильтров является то, что для достижения заданного уровня производительности они часто требуют гораздо более высокого порядка фильтрации, чем БИХ-фильтры. Соответственно, задержка этих фильтров часто намного больше, чем для БИХ-фильтра равной производительности.
Фильтры FIR
Метод проектирования фильтра | Описание | Функции фильтра |
|---|---|---|
Работа с окнами | Применить окно к усеченному обратному преобразованию Фурье указанного фильтра «кирпичной стены» | |
Многополосный с переходными полосами | Равномерный или наименьший подход квадратов по поддиапазонам частотного диапазона | |
Ограниченные наименьшие квадраты | Минимизация квадратичной интегральной ошибки во всем диапазоне частот с учетом ограничений максимальной погрешности | |
Произвольный ответ | Произвольные ответы, включая нелинейные фазовые и сложные фильтры | |
Приподнятый косинус | Низкопроходная реакция с плавным синусоидальным переходом |
За исключением cfirpm, все функции проектирования фильтров FIR предназначены только для линейных фазовых фильтров. Коэффициенты фильтра, или «отводы», таких фильтров подчиняются либо четному, либо нечетному соотношению симметрии. В зависимости от этой симметрии и от того, является ли порядок n фильтра четным или нечётным, линейный фазовый фильтр (хранится в векторе длины n + 1 b) имеет определенные внутренние ограничения на его частотную характеристику.
| Тип фильтра линейной фазы | Порядок фильтрации | Симметрия коэффициентов | Ответ H (f), f = 0 | Ответ H (f), f = 1 (Найквист) |
|---|---|---|---|---|
Тип I | Даже | даже: 1,..., n + 1 | Без ограничений | Без ограничений |
Тип II | Странный | даже: 1,..., n + 1 | Без ограничений | H (1) |
Тип III | Даже | нечетные: = 1,..., n + 1 | H (0) | H (1) |
Тип IV | Странный | нечетные: = 1,..., n + 1 | H (0) | Без ограничений |
Фазовая задержка и групповая задержка линейных фазовых КИХ-фильтров равны и постоянны в полосе частот. Для линейно-фазового КИХ-фильтра порядка n групповая задержка равна n/2, и отфильтрованный сигнал просто задерживается на n/2 временных шага (и величина его преобразования Фурье масштабируется по амплитудной характеристике фильтра). Это свойство сохраняет форму волны сигналов в полосе пропускания; то есть фазовое искажение отсутствует.
Функции fir1, fir2, firls, firpm, fircls, и fircls1 все линейные фильтры FIR типов I и II по умолчанию. rcosdesign проектирует только фильтры типа I. Оба firls и firpm линейные фазовые фильтры FIR типа III и IV конструкции 'hilbert' или 'differentiator' флаг. cfirpm может конструировать линейный фазовый фильтр любого типа, а также нелинейные фазовые фильтры.
Примечание
Поскольку частотная характеристика фильтра типа II равна нулю на частоте Найквиста («высокая» частота), fir1 не проектирует фильтры верхних и верхних частот типа II. Для нечетных значений n в этих случаях, fir1 добавляет 1 к порядку и возвращает фильтр типа I.
Рассмотрим идеальный, или «кирпичная стена», цифровой фильтр нижних частот с частотой отсечения, равной λ 0 рад/с. Этот фильтр имеет 1 амплитуды на всех частотах с величиной, меньшей λ 0, и 0 амплитуды на частотах с величиной, находящейся в диапазоне λ 0 и λ. Его последовательность импульсной характеристики h (n)
ejωndω=12π∫−ω0ω0ejωndω=sinω0nπn
Этот фильтр не может быть реализован, так как его импульсная характеристика является бесконечной и некаузальной. Чтобы создать импульсную характеристику с конечной длительностью, усечите ее, применив окно. Сохраняя центральный участок импульсной характеристики в этом усечении, получается линейный фазовый КИХ-фильтр. Например , фильтр длиной 51 с частотой отсечки нижних частот, которая составляет 0,4 δ рад/с, является
b = 0.4*sinc(0.4*(-25:25));
Примененное здесь окно представляет собой простое прямоугольное окно. По теореме Парсеваля, это фильтр длины 51, который лучше всего аппроксимирует идеальный фильтр нижних частот, в интегрированном смысле наименьших квадратов. Следующая команда отображает частотную характеристику фильтра в FVTool:
fvtool(b,1)
Обратите внимание, что ось Y, показанная на рисунке ниже, находится в квадрате величины. Это можно задать, щелкнув правой кнопкой мыши на метке оси и выбрав в меню Значение в квадрате (Magnitude Squared).
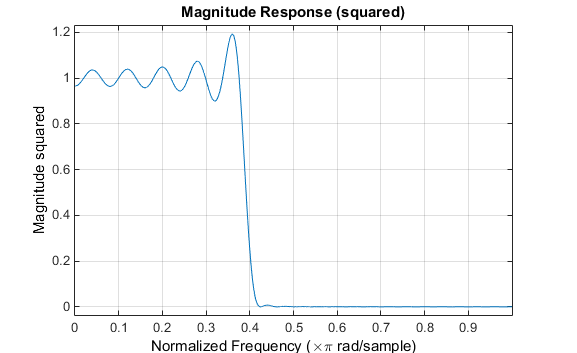
В ответе возникают звон и рябь, особенно вблизи края полосы. Этот «эффект Гиббса» не исчезает по мере увеличения длины фильтра, но непрямоугольное окно уменьшает его величину. Умножение на окно во временной области вызывает свертку или сглаживание в частотной области. Примените к фильтру окно Hamming длиной 51 и просмотрите результат с помощью команды FVTool:
b = 0.4*sinc(0.4*(-25:25)); b = b.*hamming(51)'; fvtool(b,1)
Обратите внимание, что ось Y, показанная на рисунке ниже, находится в квадрате величины. Это можно задать, щелкнув правой кнопкой мыши на метке оси и выбрав в меню Значение в квадрате (Magnitude Squared).
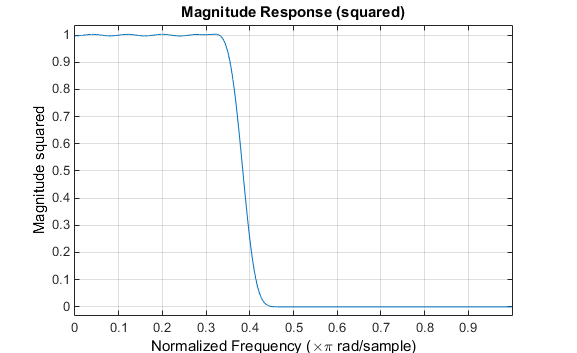
Использование окна Хэмминга значительно уменьшает количество вызывных сигналов. Это улучшение происходит за счет ширины перехода (версия с окном занимает больше времени, чтобы наклониться от полосы пропускания к полосе останова) и оптимальности (версия с окном не минимизирует интегрированную ошибку в квадрате).
fir1 использует аппроксимацию наименьших квадратов для вычисления коэффициентов фильтра и затем сглаживает импульсную характеристику окном. Обзор окон и их свойств см. в разделе Windows. fir1 напоминает функции проектирования БИХ-фильтров тем, что формулируется для проектирования фильтров в стандартных конфигурациях диапазонов: lowpass, bandpass, high pass, bandstop.
Заявления
n = 50; Wn = 0.4; b = fir1(n,Wn);
создать вектор строки b содержащий коэффициенты порядка n Фильтр с хэмминговым окном. Это низкочастотный линейный фазовый КИХ-фильтр с частотой отсечки Wn. Wn - число между 0 и 1, где 1 соответствует частоте Найквиста, равной половине частоты дискретизации. (В отличие от других методов, здесь Wn соответствует точке 6 дБ.) Для фильтра верхних частот просто добавьте 'high' в список параметров функции. Для полосового или полосового фильтра укажите Wn в виде двухэлементного вектора, содержащего граничные частоты полосы пропускания. Приложить 'stop' для конфигурации bandstop.
b = fir1(n,Wn,window) использует окно, указанное в векторе столбца window для проекта. Вектор window должно быть n+1 элементы длиной. Если окно не указано, fir1 применяет окно Хэмминга.
Оценка порядка окна Кайзера. kaiserord функция оценивает порядок фильтра, частоту отсечки и бета-параметр окна Кайзера, необходимый для соответствия заданному набору спецификаций. Учитывая вектор рёбер полосы частот и соответствующий вектор величин, а также максимально допустимую пульсацию, kaiserord возвращает соответствующие входные параметры для fir1 функция.
fir2 функция также проектирует оконные КИХ-фильтры, но с произвольно сформированной кусочно-линейной частотной характеристикой. Это в отличие от fir1, который проектирует фильтры только в стандартных конфигурациях нижних, верхних и полосовых частот.
Команды
n = 50; f = [0 .4 .5 1]; m = [1 1 0 0]; b = fir2(n,f,m);
вернуть вектор строки b содержащий n+1 коэффициенты порядка n КИХ-фильтр, частотно-амплитудные характеристики которого совпадают с заданными векторами f и m. f - вектор частотных точек в диапазоне от 0 до 1, где 1 представляет частоту Найквиста. m - вектор, содержащий заданную амплитудную характеристику в точках, указанных в f. (Аналогом IIR этой функции является yulewalk, который также проектирует фильтры на основе произвольных кусочно-линейных амплитудных откликов. Дополнительные сведения см. в разделе Конструкция фильтра IIR.)
firls и firpm функции предоставляют более общие средства определения идеального указанного фильтра, чем fir1 и fir2 функции. Эти функции конструируют трансформаторы Гильберта, дифференциаторы и другие фильтры с нечетными симметричными коэффициентами (линейная фаза типа III и типа IV). Они также позволяют включать переходные или «не волнующие» области, в которых ошибка не минимизирована, и выполнять зависящее от полосы взвешивание минимизации.
firls функция является расширением fir1 и fir2 функция заключается в том, что она минимизирует интеграл квадрата ошибки между заданной частотной характеристикой и фактической частотной характеристикой.
firpm функция реализует алгоритм Паркса - Макклеллана, который использует алгоритм обмена Ремеза и теорию аппроксимации Чебышёва для проектирования фильтров с оптимальными соответствиями между заданными и фактическими частотными откликами. Фильтры оптимальны в том смысле, что минимизируют максимальную ошибку между заданной частотной характеристикой и фактической частотной характеристикой; иногда их называют минимаксными фильтрами. Фильтры, сконструированные таким образом, демонстрируют чёткое поведение в своей частотной характеристике и, следовательно, также известны как чёткие фильтры. Алгоритм проектирования КИХ-фильтра Паркса-Макклеллана, возможно, является наиболее популярной и широко используемой методологией проектирования КИХ-фильтра.
Синтаксис для firls и firpm то же самое; единственное отличие заключается в их схемах минимизации. В следующем примере показано, как фильтры проектируются с помощью firls и firpm отражают эти различные схемы.
Режим работы по умолчанию firls и firpm используется для проектирования фильтров линейной фазы типа I или типа II в зависимости от того, является ли требуемый порядок четным или нечетным, соответственно. Примером нижних частот с аппроксимированной амплитудой 1 от 0 до 0,4 Гц и аппроксимированной амплитудой 0 от 0,5 до 1,0 Гц является
n = 20; % Filter order f = [0 0.4 0.5 1]; % Frequency band edges a = [1 1 0 0]; % Amplitudes b = firpm(n,f,a);
от 0,4 до 0,5 Гц, firpm не выполняет минимизацию ошибок; это переходная полоса или область «не волнуют». Полоса перехода сводит к минимуму ошибку больше в полосах, которые вас волнуют, за счет более медленной скорости перехода. Таким образом, фильтры этих типов имеют присущий им компромисс, аналогичный конструкции КИХ посредством оконной обработки.
Для сравнения наименьших квадратов с одинаковой конструкцией фильтра используйте firls для создания аналогичного фильтра. Напечатать
bb = firls(n,f,a);
и сравнить их частотные характеристики с помощью FVTool:
fvtool(b,1,bb,1)
Обратите внимание, что ось Y, показанная на рисунке ниже, находится в квадрате величины. Это можно задать, щелкнув правой кнопкой мыши на метке оси и выбрав в меню Значение в квадрате (Magnitude Squared).
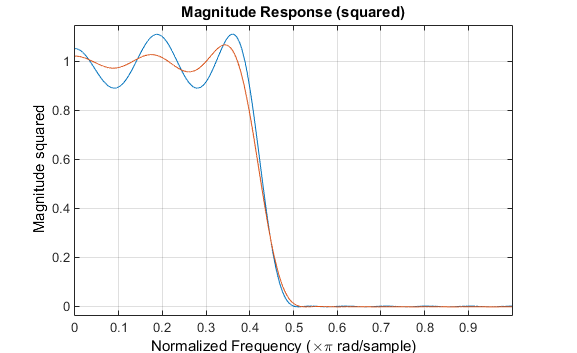
Фильтр разработан с firpm проявляет чёткое поведение. Также обратите внимание, что firls фильтр имеет лучший отклик по большей части полосы пропускания и полосы останова, но на краях полосы (f = 0.4 и f = 0.5), ответ дальше от идеала, чем firpm фильтр. Это показывает, что firpm максимальная ошибка фильтра над полосой пропускания и полосой останова меньше, и фактически она является наименьшей возможной для этой конфигурации края полосы частот и длины фильтра.
Считайте полосы частот линиями на коротких частотных интервалах. firpm и firls используйте эту схему для представления любой кусочно-линейной частотно-ответной функции с любыми переходными полосами. firls и firpm проектирование низкочастотных, высокопроходных, полосовых и полосовых фильтров; пример полосы пропускания:
f = [0 0.3 0.4 0.7 0.8 1]; % Band edges in pairs a = [0 0 1 1 0 0]; % Bandpass filter amplitude
Технически, эти f и a векторы определяют пять полос:
Две стопорные полосы, от 0,0 до 0,3 и от 0,8 до 1,0
Полоса пропускания от 0,4 до 0,7
Две переходные полосы, от 0,3 до 0,4 и от 0,7 до 0,8
Примеры фильтров верхних и нижних частот:
f = [0 0.7 0.8 1]; % Band edges in pairs a = [0 0 1 1]; % Highpass filter amplitude f = [0 0.3 0.4 0.5 0.8 1]; % Band edges in pairs a = [1 1 0 0 1 1]; % Bandstop filter amplitude
Пример многополосного полосного фильтра:
f = [0 0.1 0.15 0.25 0.3 0.4 0.45 0.55 0.6 0.7 0.75 0.85 0.9 1]; a = [1 1 0 0 1 1 0 0 1 1 0 0 1 1];
Другой возможностью является фильтр, который имеет в качестве переходной области линию, соединяющую полосу пропускания с полосой останова; это может помочь контролировать отклик «бегущей» величины в широких переходных регионах:
f = [0 0.4 0.42 0.48 0.5 1]; a = [1 1 0.8 0.2 0 0]; % Passband, linear transition, % stopband
Оба firls и firpm позволяют сделать более или менее акцент на минимизации погрешности в определенных полосах частот относительно других. Для этого задайте весовой вектор, следующий за частотным и амплитудным векторами. Пример низкопроходного равнопроходного фильтра с в 10 раз меньшей пульсацией в полосе останова, чем полоса пропускания
n = 20; % Filter order f = [0 0.4 0.5 1]; % Frequency band edges a = [1 1 0 0]; % Amplitudes w = [1 10]; % Weight vector b = firpm(n,f,a,w);
Допустимый весовой вектор всегда равен половине длины f и a векторы; на полосу должен быть ровно один вес.
При вызове с завершающим 'h' или 'Hilbert' опция, firpm и firls конструировать фильтры FIR с нечётной симметрией, то есть фильтры типа III (для чётного порядка) или типа IV (для нечётного порядка) линейные фазовые фильтры. Идеальный преобразователь Гильберта обладает свойством антисимметрии и амплитудой 1 во всем диапазоне частот. Попробуйте следующие приблизительные трансформаторы Гильберта и постройте их график с помощью FVTool:
b = firpm(21,[0.05 1],[1 1],'h'); % Highpass Hilbert bb = firpm(20,[0.05 0.95],[1 1],'h'); % Bandpass Hilbert fvtool(b,1,bb,1)
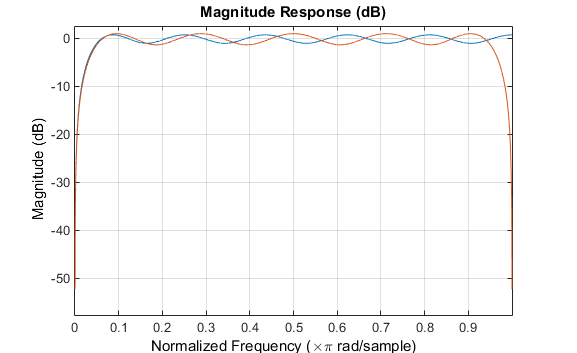
Можно найти задержанное преобразование Гильберта сигнала x пропуская его через эти фильтры.
fs = 1000; % Sampling frequency t = (0:1/fs:2)'; % Two second time vector x = sin(2*pi*300*t); % 300 Hz sine wave example signal xh = filter(bb,1,x); % Hilbert transform of x
Аналитический сигнал, соответствующий x является сложным сигналом, который имеет x как его реальная часть и преобразование Гильберта x в качестве его мнимой части. Для этого метода FIR (альтернатива hilbert функция), необходимо задержать x на половину порядка фильтра для создания аналитического сигнала:
xd = [zeros(10,1); x(1:length(x)-10)]; % Delay 10 samples xa = xd + j*xh; % Analytic signal
Этот метод не работает непосредственно для фильтров нечетного порядка, которые требуют неинтегрированной задержки. В этом случае hilbert функция, описанная в преобразовании Гильберта, оценивает аналитический сигнал. В качестве альтернативы используйте resample функция задержки сигнала на неинтегрированное число выборок.
Дифференцирование сигнала во временной области эквивалентно умножению преобразования Фурье сигнала на мнимую линейную функцию. То есть, чтобы дифференцировать сигнал, пропустить его через фильтр, который имеет отклик H (λ) = jλ. Аппроксимировать идеальный дифференциатор (с задержкой) с помощью firpm или firls с 'd' или 'differentiator' вариант:
b = firpm(21,[0 1],[0 pi],'d');
Для фильтра типа III полоса дифференциации должна останавливаться без частоты Найквиста, и амплитудный вектор должен отражать это изменение, чтобы обеспечить правильный наклон:
bb = firpm(20,[0 0.9],[0 0.9*pi],'d');
В 'd' режим, firpm взвешивает ошибку на 1/λ в ненулевых диапазонах амплитуд, чтобы минимизировать максимальную относительную ошибку. firls весит ошибку на (1/λ) 2 в ненулевых диапазонах амплитуд в 'd' режим.
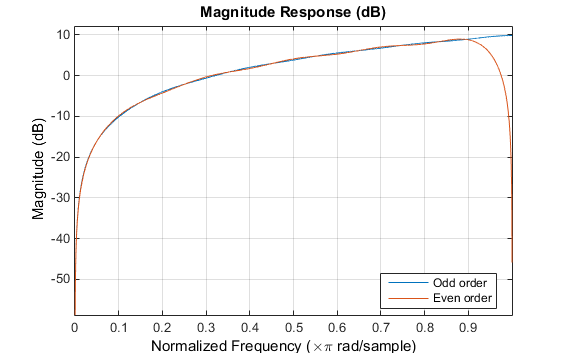
На следующих графиках показаны отклики величины для указанных выше дифференциаторов.
fvtool(b,1,bb,1) legend('Odd order','Even order','Location','best')
Функции проектирования КИХ-фильтра с ограничением по наименьшим квадратам (CLS) реализуют метод, который позволяет проектировать КИХ-фильтры без явного определения переходных полос для отклика величины. Возможность опустить спецификацию переходных полос полезна в нескольких ситуациях. Например, может быть неясно, где должна появиться жестко определенная переходная полоса, если шумовая и сигнальная информация появляются вместе в одной и той же полосе частот. Аналогично, может иметь смысл опустить спецификацию переходных полос, если они кажутся только для контроля результатов явлений Гиббса, которые появляются в отклике фильтра. Для обсуждения этого метода см. Selesnick, Lang и Burrus [2].
Вместо того, чтобы определить полосы пропускания, полосы задерживания и регионы перехода, метод CLS принимает частоту среза (для highpass, lowpass, полосно-пропускающих, или bandstop случаев), или полоса пропускания и края полосы задерживания (для многополосных случаев), для ответа, который Вы определяете. Таким образом, метод CLS определяет переходные области неявно, а не явно.
Ключевой особенностью метода CLS является то, что он позволяет определить верхний и нижний пороги, которые содержат максимально допустимую пульсацию в отклике величины. Учитывая это ограничение, метод применяет метод минимизации ошибок наименьшего квадрата в частотном диапазоне отклика фильтра, а не в определенных диапазонах. Минимизация ошибок включает в себя любые области неоднородности в идеальной реакции «кирпичной стены». Дополнительное преимущество заключается в том, что метод позволяет указать произвольно небольшие пики, возникающие в результате явления Гиббса.
Существует две функции набора инструментов, реализующие этот метод проектирования.
Описание | Функция |
|---|---|
Конструкция фильтра FIR с наименьшим квадратным диапазоном | |
Ограниченная конструкция фильтра с наименьшим квадратом для низкочастотных и высокочастотных линейных фазовых фильтров |
Для получения подробной информации о синтаксисе вызова для этих функций см. описание их ссылок в справочнике по функциям.
Основные функции проектирования CLS, fircls1, использует этот метод для проектирования низкочастотных и высокочастотных фильтров FIR. В качестве примера рассмотрим проектирование фильтра с импульсной характеристикой порядка 61 и частотой отсечки 0,3 (нормализованной). Кроме того, определите верхнюю и нижнюю границы, ограничивающие процесс конструирования, как:
Максимальное отклонение полосы пропускания от 1 (пульсация полосы пропускания) 0,02.
Максимальное отклонение полосы останова от 0 (пульсация полосы останова) 0,008.
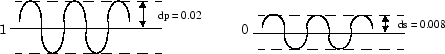
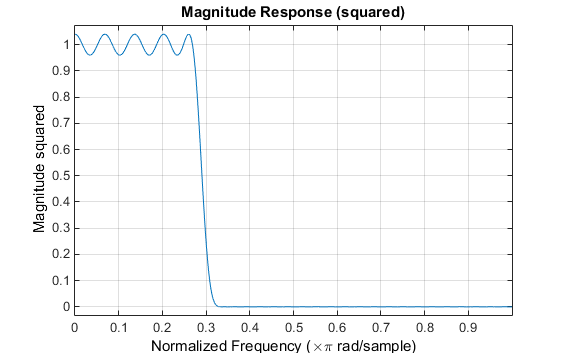
Для решения этой проблемы с конструкцией используйте fircls1используйте следующие команды:
n = 61; wo = 0.3; dp = 0.02; ds = 0.008; h = fircls1(n,wo,dp,ds); fvtool(h,1)
Обратите внимание, что ось Y, показанная ниже, находится в квадрате величины. Это можно задать, щелкнув правой кнопкой мыши на метке оси и выбрав в меню Значение в квадрате (Magnitude Squared).
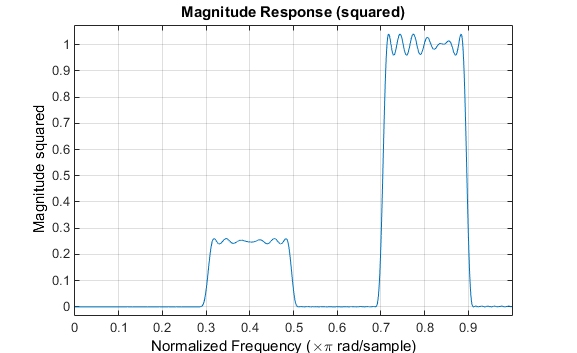
fircls использует тот же метод для проектирования КИХ-фильтров с заданной кусочно-постоянной амплитудной характеристикой. В этом случае можно задать вектор ребер полосы и соответствующий вектор амплитуд полосы. Кроме того, можно указать максимальное количество пульсаций для каждой полосы.
Например, предположим, что спецификации для вызова фильтра:
От 0 до 0,3 (нормализовано): амплитуда 0, верхняя граница 0,005, нижняя граница -0,005
От 0,3 до 0,5: амплитуда 0,5, верхняя граница 0,51, нижняя граница 0,49
От 0,5 до 0,7: амплитуда 0, верхняя граница 0,03, нижняя граница -0,03
От 0,7 до 0,9: амплитуда 1, верхняя граница 1,02, нижняя граница 0,98
От 0,9 до 1: амплитуда 0, верхняя граница 0,05, нижняя граница -0,05
Сконструировать фильтр CLS с порядком 129 импульсной характеристики, который соответствует следующим спецификациям:
n = 129; f = [0 0.3 0.5 0.7 0.9 1]; a = [0 0.5 0 1 0]; up = [0.005 0.51 0.03 1.02 0.05]; lo = [-0.005 0.49 -0.03 0.98 -0.05]; h = fircls(n,f,a,up,lo); fvtool(h,1)
Обратите внимание, что ось Y, показанная ниже, находится в квадрате величины. Это можно задать, щелкнув правой кнопкой мыши на метке оси и выбрав в меню Значение в квадрате (Magnitude Squared).
Взвешенная конструкция фильтра CLS позволяет проектировать низкочастотные или высокочастотные фильтры FIR с относительным взвешиванием минимизации ошибок в каждой полосе. fircls1 функция позволяет задать границы полосы пропускания и полосы останова для функции взвешивания наименьших квадратов, а также константу k задает отношение коэффициента отсчета полосы останова к коэффициенту взвешивания полосы пропускания.
Например, рассмотрим спецификации, которые вызывают фильтр FIR с порядком импульсной характеристики 55 и частотой отсечки 0,3 (нормализованный). Также допустим максимально допустимую пульсацию полосы пропускания 0,02 и максимально допустимую пульсацию полосы останова 0,004. Кроме того, добавьте требования к взвешиванию:
Край полосы пропускания для весовой функции 0,28 (нормализовано)
Край полосы останова для весовой функции 0,32
Минимизация весовых ошибок в полосе останова в 10 раз больше, чем в полосе пропускания
Чтобы подойти к этому с помощью fircls1, тип
n = 55; wo = 0.3; dp = 0.02; ds = 0.004; wp = 0.28; ws = 0.32; k = 10; h = fircls1(n,wo,dp,ds,wp,ws,k); fvtool(h,1)
Обратите внимание, что ось Y, показанная ниже, находится в квадрате величины. Это можно задать, щелкнув правой кнопкой мыши на метке оси и выбрав в меню Значение в квадрате (Magnitude Squared).
cfirpm функция проектирования фильтра обеспечивает инструмент для проектирования фильтров FIR с произвольными сложными ответами. Он отличается от других функций конструкции фильтра тем, как задана частотная характеристика фильтра: он принимает имя функции, которая возвращает характеристику фильтра, вычисленную по сетке частот. Эта возможность делает cfirpm очень универсальная и мощная технология для конструкции фильтра.
Этот метод конструирования может быть использован для получения нелинейно-фазовых КИХ-фильтров, асимметричных частотно-ответных фильтров (со сложными коэффициентами) или более симметричных фильтров с пользовательскими частотными откликами.
Алгоритм проектирования оптимизирует ошибку Чебышёва (или минимакса), используя расширенный алгоритм Ремеза-обмена для начальной оценки. Если этому методу обмена не удается получить оптимальный фильтр, алгоритм переключается на алгоритм подъема-спуска, который берет на себя выполнение сходимости к оптимальному решению.
Рассмотрим многополосный фильтр со следующими специальными характеристиками частотной области.
Группа | Амплитуда | Взвешивание оптимизации |
|---|---|---|
[–1 –0.5] | [5 1] | 1 |
[–0.4 +0.3] | [2 2] | 10 |
[+0.4 +0.8] | [2 1] | 5 |
Линейно-фазовый многополосный фильтр может быть сконструирован с использованием предопределенной функции частотного отклика. multiband, следующим образом:
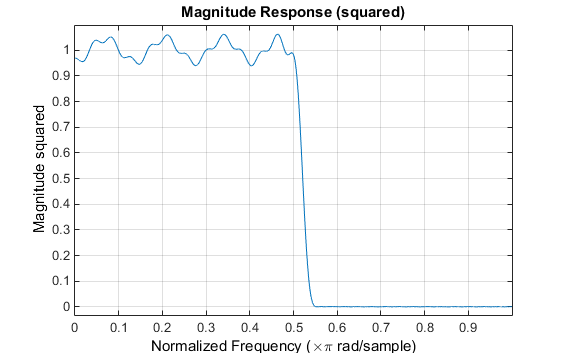
b = cfirpm(38, [-1 -0.5 -0.4 0.3 0.4 0.8], ... {'multiband', [5 1 2 2 2 1]}, [1 10 5]);
Для конкретного случая многополосного фильтра можно использовать краткую нотацию конструкции фильтра, подобную синтаксису для firpm:
b = cfirpm(38,[-1 -0.5 -0.4 0.3 0.4 0.8], ...
[5 1 2 2 2 1], [1 10 5]);
Как и с firpm, вектор ребер полосы передается в cfirpm. Этот вектор определяет полосы частот, в которых выполняется оптимизация; Следует отметить, что существуют две переходные полосы, от -0,5 до -0,4 и от 0,3 до 0,4.
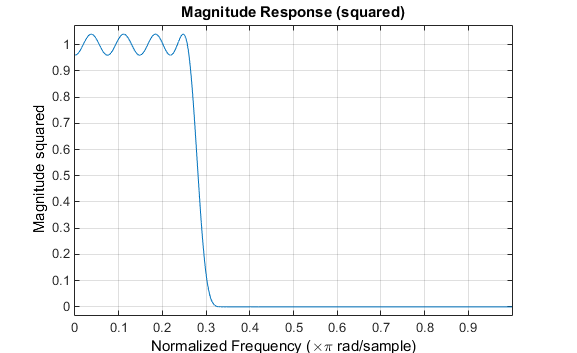
В любом случае частотную характеристику получают и строят с использованием линейного масштаба в FVTool:
fvtool(b,1)
Обратите внимание, что диапазон данных, показанный ниже, (-pi,pi).
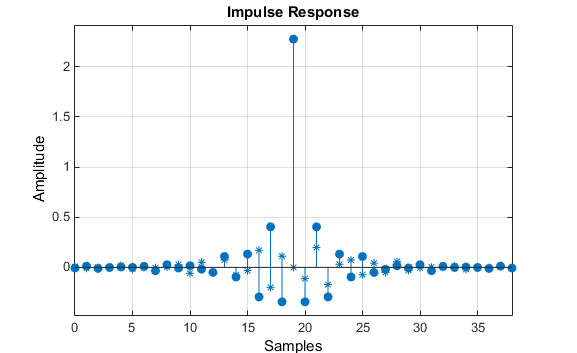
Отклик фильтра для этого многополосного фильтра является сложным, что ожидается из-за асимметрии в частотной области. Импульсная характеристика, которую можно выбрать на панели инструментов FVTool, показана ниже.
Рассмотрим конструкцию 62-отводного фильтра нижних частот с половинной отсечкой Найквиста. Если задать отрицательное значение смещения для lowpass функция конструкции фильтра, смещение групповой задержки для конструкции значительно меньше, чем полученное для стандартной линейно-фазовой конструкции. Эта конструкция фильтра может быть вычислена следующим образом:
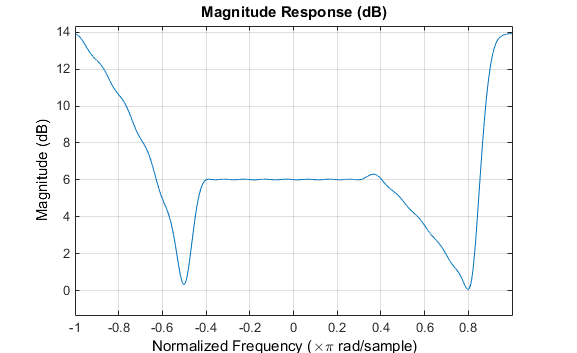
b = cfirpm(61,[0 0.5 0.55 1],{'lowpass',-16});
Результирующий отклик величины равен
fvtool(b,1)
Ось Y находится в квадрате величины, который можно задать, щелкнув правой кнопкой мыши на метке оси и выбрав в меню Значение в квадрате (Magnitude Squared).
Групповая задержка фильтра показывает, что смещение было уменьшено от N/2 кому N/2-16 (т.е. от 30.5 кому 14.5). Однако теперь задержка группы больше не является плоской в области полосы пропускания. Чтобы создать этот график, нажмите кнопку «Ответ на групповую задержку» на панели инструментов.
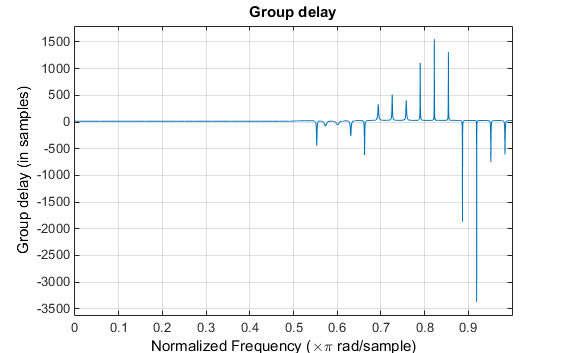
Если сравнить этот нелинейно-фазовый фильтр с линейно-фазовым фильтром, который имеет точно 14,5 выборки групповой задержки, результирующий фильтр будет порядка 2 * 14,5, или 29. Используяb = cfirpm(29,[0 0.5 0.55 1],'lowpass'), полоса пропускания и пульсация полосы останова намного больше для фильтра порядка 29. Эти сравнения помогут определить, какой фильтр более подходит для конкретного приложения.