Критически дискретизированные и избыточно дискретизированные банки вейвлет-фильтров

Банки вейвлет-фильтров - это особые случаи банков многоскоростных фильтров, называемых банками фильтров с древовидной структурой. В блоке фильтров два или более фильтра подаются на входной сигнал, и выходные сигналы фильтра обычно дискретизируются с понижением частоты. На следующем рисунке показаны два этапа или уровня набора фильтров анализа с критической выборкой из двухканального дерева. Фильтры изображены в области z.

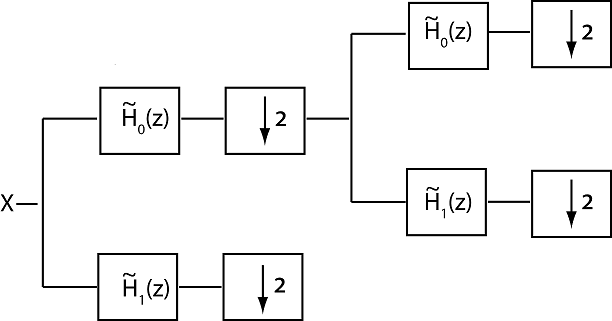
Функции системы фильтров ${\overset{}{}}_{H˜0} (z$ ) и ${\overset{}{}}_{} H˜1 ($ z) обычно предназначены для приблизительно разделения входного сигнала X на несвязанные поддиапазоны. В банках фильтров, структурированных в вейвлет-дереве, ${\overset{}{фильтр}}_{} H˜0$ (z) является фильтром нижних частот, или масштабированием, с ненулевой частотной характеристикой на интервале [-δ/2, λ/2] радианов/выборок или [-1/4, 1/4] циклов/выборок. ${\overset{Фильтр}{}}_{} H˜1$ (z) является фильтром верхних частот, или вейвлет, с ненулевым частотным откликом на интервале [-δ, -λ/2] ∪ [λ/2] радианов/выборок или [-1/2, -1/4] ∪ [1/4, 1/2] циклов/выборок. Блок фильтров выполняет итерацию на выходе фильтра анализа нижних частот для получения последовательных уровней, что приводит к приблизительной октавной фильтрации входного сигнала. Два фильтра анализа не идеальны, что приводит к наложению псевдонимов, которые должны быть отменены соответствующим образом разработанными фильтрами синтеза для идеальной реконструкции. Для набора ортогональных фильтров объединение масштабного фильтра и его четных сдвигов и вейвлет-фильтра и его четных сдвигов образует ортонормированный базис для пространства квадратно-суммируемых ${последовательностей}^{,} ℓ2$ (ℤ). Фильтры синтеза являются обратными по времени и сопряженными фильтрами анализа. Для банков биортогенных фильтров фильтры синтеза и их четные сдвиги образуют обратную или двойственную основу для фильтров анализа. При использовании двух фильтров анализа понижение дискретизации выходного сигнала каждого фильтра анализа на два на каждом этапе гарантирует, что общее количество выходных выборок равно количеству входных выборок. Случай, когда количество фильтров анализа равно коэффициенту понижающей дискретизации, называется критической выборкой. Банк фильтров анализа, в котором количество каналов больше, чем коэффициент понижающей дискретизации, является банком фильтров с избыточной выборкой.

Вейвлет-преобразование с двойной плотностью

Следующий рисунок иллюстрирует два уровня набора фильтров анализа с избыточной выборкой с тремя каналами и коэффициентом понижающей дискретизации, равным двум. Фильтры изображены в области z.

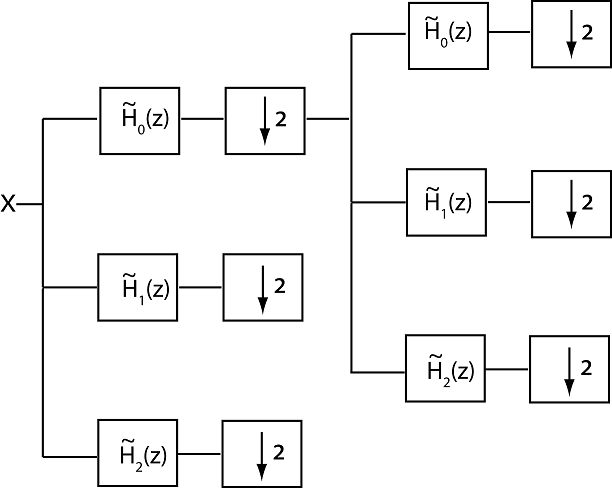
Предположим, что фильтр ${\overset{}{}}_{H˜0} (z$ ) является фильтром полуполосы нижних частот, а фильтры ${\overset{}{}}_{} H˜1 ($ z) ${\overset{}{и}}_{} H˜2$ (z) являются фильтрами полуполосы верхних частот.

Предположим, что три фильтра вместе с соответствующими фильтрами синтеза образуют идеальный банк фильтров реконструкции. Если дополнительно, ${\overset{}{}}_{H˜1} (z$ ) и ${\overset{}{}}_{} H˜2 ($ z) генерируют вейвлеты, удовлетворяющие следующему соотношению

$_{λ 1} (t)_{=} λ 2 (t -$ 1/2),

банк фильтров реализует вейвлет-преобразование с двойной плотностью. Предыдущее условие гарантирует, что целочисленные трансляции одного вейвлета падают на полпути между целыми трансляциями второго вейвлета. В теоретических терминах кадра вейвлет-преобразование с двойной плотностью реализует жесткое расширение кадра.

Следующий код иллюстрирует два вейвлета, используемых в вейвлет-преобразовании с двойной плотностью.

x = zeros(256,1);
df = dtfilters('filters1');
wt1 = dddtree('ddt',x,5,df,df);
wt2 = dddtree('ddt',x,5,df,df);
wt1.cfs{5}(5,1,1) = 1;
wt2.cfs{5}(5,1,2) = 1;
wav1 = idddtree(wt1);
wav2 = idddtree(wt2);
plot(wav1); hold on;
plot(wav2,'r'); axis tight;
legend('\psi_1(t)','\psi_2(t)')

Нельзя произвольно выбрать два вейвлет-фильтра для реализации вейвлет-преобразования с двойной плотностью. Три фильтра анализа и синтеза должны удовлетворять идеальным условиям реконструкции (PR). Для трех вещественных фильтров условия PR:

$\begin{array}{l} _{H0} (z)_{} H0 ({1/z}_{)} +_{H1} (z) {H1}_{} ({1/z}_{)} + H2 ( \\ z_{)} H2_{(} 1/z) =_{} 2H0 (z_{)} H0 (-_{} 1/z) +_{} H1 (z) \end{array}$ H1 (− 1/z) + H2 (z) H2 (− 1/z) = 0

Можно получить вейвлет-анализ и кадры синтеза для вейвлет-преобразования двойной плотности с 6 и 12 отводами, используя dtfilters.

[df1,sf1] = dtfilters('filters1');
[df2,sf2] = dtfilters('filters2');

df1 и df2 представляют собой трехколонные матрицы, содержащие фильтры анализа. Первый столбец содержит фильтр масштабирования, а второй и третий столбцы содержат вейвлет-фильтры. Соответствующие фильтры синтеза находятся в sf1 и sf2.

Для получения подробной информации о формировании вейвлет-кадров для вейвлет-преобразования с двойной плотностью см. [4] и [5].

Основными преимуществами вейвлет-преобразования с двойной плотностью по сравнению с критически дискретизированным дискретным вейвлет-преобразованием являются

Снижение чувствительности к сдвигу
Уменьшенные прямоугольные артефакты в преобразовании 2-D
Более плавные вейвлеты для заданного числа моментов исчезновения

Основные недостатки:

Увеличение вычислительных затрат
Неоргональное преобразование

Кроме того, несмотря на то, что он демонстрирует меньшую чувствительность к сдвигу, чем критически дискретизированный DWT, DWT двойной плотности не является инвариантным сдвигом, как комплексное вейвлет-преобразование двойного дерева. Вейвлет-преобразование двойной плотности также не имеет направленной избирательности ориентированных вейвлет-преобразований двойного дерева.

Комплексное вейвлетное преобразование с двойным деревом

Критически дискретизированное дискретное вейвлет-преобразование (DWT) страдает от отсутствия инвариантности сдвига в 1-D и направленной чувствительности в N-D. Эти недостатки можно устранить, используя приблизительно аналитические вейвлеты. Аналитический вейвлет определяется как

$_{ψc} (t)_{=} ψr {(t)}_{}$ +jψi (t)

где j обозначает мнимую единицу. Мнимая часть вейвлета, _{λ i} (t), является преобразованием Гильберта действительной части,, (_t). В частотной области аналитический вейвлет имеет поддержку только на половине частотной оси. Это означает, что аналитический вейвлет λ c (t) имеет только половину полосы пропускания действительного _{вейвлета} (t).

Невозможно получить точно аналитические вейвлеты, генерируемые КИХ-фильтрами. Преобразования Фурье компактно поддерживаемых вейвлетов не могут исчезнуть ни на одном наборе ненулевых измерений. Это означает, что преобразование Фурье не может быть нулевым на отрицательной частотной оси. Кроме того, эффективная двухканальная реализация банка фильтров DWT вытекает из следующего идеального условия реконструкции для масштабного фильтра, $_{H0} (^{} ej$

$|_{} H0^{(} {ejλ}^{)} |_{2} +^{| H0} (^{ej} (λ$ + δ)) | 2 = 2.

Если вейвлет, связанный с MRA, является аналитическим, функция масштабирования также является аналитическим. Это подразумевает, что

$_{H0} (^{} ejü) = 0$ −π≤ω<0,

из чего следует, что $|_{} H0^{(} {ejü}^{)} | 2 = 2$ 0≤ω≤π. В результате фильтр масштабирования будет allpass.

Предыдущие результаты показывают, что вы не можете найти компактно поддерживающий вейвлет, определенный фильтрами FIR, который является точно аналитическим. Однако можно получить вейвлеты, которые являются приблизительно аналитическими, путем объединения двух банков фильтров с древовидной структурой, если фильтры в преобразовании с двойным деревом тщательно сконструированы для удовлетворения определенных условий [1], [6].

Комплексное вейвлет-преобразование двойного дерева реализовано двумя отдельными двухканальными блоками КИХ-фильтров. Выход одного блока фильтров считается действительной частью, в то время как выход другого блока фильтров является мнимой частью. Поскольку комплексное вейвлет-преобразование двойного дерева использует два критически дискретизированных блока фильтров, избыточность является ^2d для d-мерного сигнала (изображения). Существует несколько критических соображений при реализации комплексного вейвлет-преобразования с двойным деревом. Для удобства см. два дерева: дерево A и дерево B.

Фильтры анализа на первом этапе каждого набора фильтров должны отличаться от фильтров, используемых на последующих этапах в обоих деревьях. Не важно, какие масштабные и вейвлет-фильтры используются в двух деревьях для этапа 1. В обоих деревьях можно использовать один и тот же первый каскад масштабирования и вейвлет-фильтров.
Фильтр масштабирования в дереве B для этапов ≥ 2 должен аппроксимировать задержку 1/2 выборки фильтра масштабирования в дереве A. Условие задержки половины выборки является необходимым и достаточным условием для соответствующего вейвлета дерева B, чтобы быть преобразованием Гильберта вейвлета дерева A. [3].

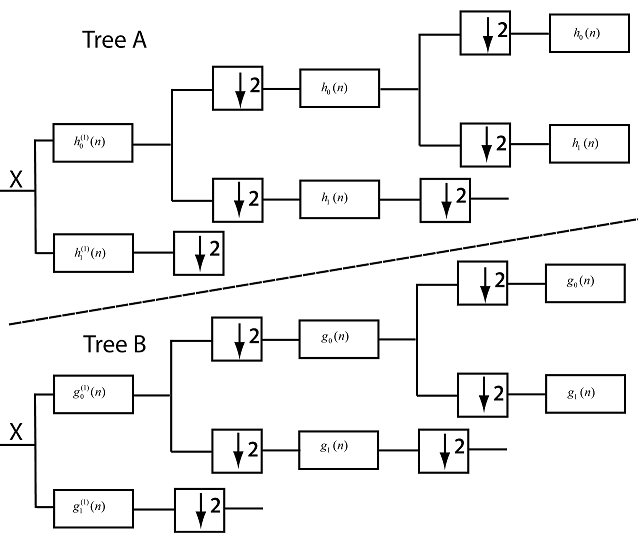
На следующем рисунке показаны три этапа набора фильтров анализа для 1-D комплексного вейвлет-преобразования двойного дерева. Фильтры масштабирования FIR для двух деревьев обозначаются как ${_{h0} (n),_{g0} (n$ )}. Импульсные фильтры КИХ для двух деревьев обозначаются как ${_{} h1 (n)_{,} g1$ (n)}. Два фильтра масштабирования предназначены для приблизительно удовлетворения условия задержки половины выборки.

$_{g0} (n)_{=} h0 (n$ − 1/2)

Надстрочный индекс (1) означает, что фильтры первой ступени должны отличаться от фильтров, используемых на последующих стадиях. Для первого этапа можно использовать любую допустимую пару масштабирование-вейвлет-фильтр. Фильтры ${_{h0} (n),_{g0} (n)$ } не могут быть произвольными фильтрами масштабирования и обеспечивают преимущества использования приблизительно аналитических вейвлетов.

2-D Вейвлет-преобразования с двойным деревом

Вейвлет-преобразование с двойным деревом с приблизительно аналитическими вейвлетами обеспечивает существенные преимущества по сравнению с разделяемым 2-D DWT для обработки изображения. Традиционный разделяемый 2-D DWT страдает картонными артефактами из-за симметричной частотной поддержки действительных (неаналитических) функций масштабирования и вейвлетов. Кроме того, критически дискретизированному разделяемому 2-D DWT не хватает инвариантности сдвига, как это делает 1-D критически дискретизированный DWT. Программное обеспечение Wavelet Toolbox™ поддерживает два варианта двойного дерева, которое преобразовывает 2-я небольшая волна, реальная ориентированная небольшая волна двойного дерева преобразовывают, и ориентированная 2-я небольшая волна комплекса двойного дерева преобразовывают. Оба подробно описаны в [6].

Действительное ориентированное двойное древовидное преобразование состоит из двух разделяемых (фильтрация строк и столбцов) блоков вейвлет-фильтров, работающих параллельно. Комплексное ориентированное 2-D вейвлет-преобразование требует четырех разделяемых блоков вейвлет-фильтров и, следовательно, технически не является двойным древовидным преобразованием. Однако оно упоминается как преобразование с двойным деревом, поскольку оно является естественным расширением 1-D сложного преобразования с двойным деревом. Для реализации реального ориентированного вейвлет-преобразования двойного дерева используйте 'realdt' опция в dddtree2. Для реализации ориентированного комплексного преобразования двойного дерева используйте 'cplxdt' вариант.

Как реальные ориентированные, так и ориентированные сложные преобразования двойного дерева чувствительны к направленным признакам изображения. Только ориентированное комплексное преобразование двойного дерева приблизительно инвариантно сдвигу. Инвариантность сдвига не является особенностью реального ориентированного преобразования двойного дерева.

Двойное дерево с двойной плотностью вейвлет-преобразований

Двойное древовидное вейвлет-преобразование объединяет свойства двойного вейвлет-преобразования плотности и двойного вейвлет-преобразования [2].

В 1-D, двойное древовидное вейвлет-преобразование двойной плотности состоит из двух трехканальных блоков фильтров. Два вейвлета в каждом дереве удовлетворяют условиям, описанным в Double-Density Wavelet Transform. В частности, целочисленные трансляции одного вейвлета падают на полпути между целочисленными трансляциями второго вейвлета. Кроме того, вейвлеты в дереве B являются приближенным преобразованием Гильберта вейвлетов в дереве A. Для реализации двойного вейвлетного преобразования с двойной плотностью дерева для 1-D сигналов используйте 'cplxdddt' опция в dddtree. Подобно вейвлет-преобразованию с двойным деревом, вейвлет-преобразование с двойным деревом с двойной плотностью обеспечивает как реальные ориентированные, так и сложные ориентированные вейвлет-преобразования в 2-D. Чтобы получить действительное ориентированное двойное дерево с двойной плотностью вейвлет-преобразования, используйте 'realdddt' опция в dddtree2. Чтобы получить комплексное ориентированное двойное дерево с двойной плотностью вейвлет-преобразования, используйте 'cplxdddt' вариант.

Ссылки

[1] Кингсбери, Н.Г. «Сложные вейвлеты для инвариантного анализа сдвига и фильтрации сигналов». Журнал прикладного и вычислительного гармонического анализа. Том 10, номер 3, май 2001 года, стр. 234-253.

[2] Селесник, I. «Двойное вейвлет-преобразование двойной плотности». Транзакции IEEE ® при обработке сигналов. Том 52, номер 5, май 2004, стр. 1304-1314.

[3] Селесник, I. «Проектирование примерных пар преобразований Гильберта вейвлет-баз». Транзакции IEEE по обработке сигналов, том 50, номер 5, стр. 1144-1152.

[4] Селесник, И. «Двойная плотность DWT» Вейвлеты в анализе сигналов и изображений: от теории к практике (А. А. Петросян, Ф. Г. Мейер, ред.). Норвелл, Массачусетс: Академические издательства Клювера:, 2001.

[5] Абдельнор, Ф. «Обработка сигналов симметричных вейвлетов и двойных кадров», том 92, номер 5, 2012, стр. 1216-1225.

[6] Селесник, я,. Р.Г. Баранюк и Н.Г. Кингсбери. «Комплексное вейвлет-преобразование двойного дерева». Журнал обработки сигналов IEEE. Том 22, номер 6, ноябрь 2005 г., стр. 123-151.

[7] Веттерли, М. «Вейвлеты, аппроксимация и сжатие». IEEE Signal Processing Magazine, том 18, номер 5, сентябрь 2001, стр. 59-73.

См. также

dddtree | dddtree2 | dualtree | dualtree2

Связанные темы

Сложные вейвлетные преобразования с двойным деревом

Документация