Линейно-квадратичное-интегральное управление
[K,S,e] = lqi(SYS,Q,R,N)
lqi вычисляет оптимальный закон управления с обратной связью состояний для цикла отслеживания, показанного на следующем рисунке.
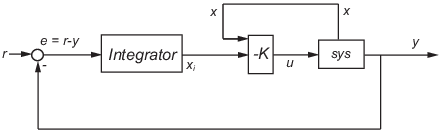
Для объекта sys с уравнениями пространства состояний (или их дискретным аналогом):
управление с обратной связью в состоянии имеет вид
где xi - выход интегратора. Этот закон управления гарантирует, что выходной y отслеживает опорную командную r. Для систем MIMO количество интеграторов равняется размерности выхода y.
[K,S,e] = lqi(SYS,Q,R,N) вычисляет оптимальную матрицу усиления K, заданную модель пространства состояний SYS для объекта управления и весовых матриц Q, R, N. Закон о контроле u = - Kz = - K [x; xi] минимизирует следующие функции затрат (для r = 0)
для непрерывного времени
для дискретного времени
В дискретном времени lqi вычисляет выходной xi интегратора с помощью прямой формулы Эйлера
где Ts - шаг расчета SYS.
Когда вы опускаете матрицу N, N установлено в 0. lqi также возвращает решение S связанного алгебраического уравнения Риккати и собственных значений с обратной связью e.
Для следующей системы в пространстве состояний с объектом с дополненным интегратором:
Данные задачи должны удовлетворять:
Пара (Aa, Ba) стабилизируема.
R > 0 и .
не имеет ненаблюдаемого режима на мнимой оси (или единичного круга в дискретном времени).
lqi поддерживает дескрипторные модели с несовпадающими E. Область выхода S от lqi - решение уравнения Риккати для эквивалентной модели явного пространства состояний
[1] P. C. Young and J. C. Willems, «An approach to the linear multivariable servomechanism problem», International Journal of Control, Volume 15, Issue 5, May 1972, pages 961-979.