Симулируйте коэффициенты регрессии и отклонение нарушения порядка байесовской линейной регрессионой модели
[ возвращает случайный вектор коэффициентов регрессии (BetaSim,sigma2Sim]
= simulate(Mdl)BetaSim) и случайное отклонение нарушения порядка (sigma2Sim), взятые из байесовской линейной регрессионой модели
Mdl β и σ2.
[ черпает из маргинальных апостериорных распределений, произведенных или обновленных путем включения данных предиктора BetaSim,sigma2Sim]
= simulate(Mdl,X,y)X и соответствующие данные отклика y.
Если Mdl является предшествующей моделью соединений, тогда simulate производит маргинальные апостериорные распределения путем обновления предыдущей модели с помощью информации о параметрах, которые она получает из данных.
Если Mdl является маргинальной апостериорной моделью, тогда simulate обновляет апостериоры с информацией о параметрах, которые они получают из дополнительных данных. Полная вероятность данных состоит из дополнительных данных X и yи данные, которые создали Mdl.
NaNs в данных указывают отсутствующие значения, которые simulate удаляет при помощи спискового удаления.
[ использует любой из комбинаций входных аргументов в предыдущих синтаксисах и дополнительные опции, заданные одним или несколькими аргументы пары "имя-значение". Для примера можно задать значение для β или σ2 для симуляции из conditional апостериорного распределения одного параметра, учитывая заданное значение другого параметра.BetaSim,sigma2Sim]
= simulate(___,Name,Value)
[ также возвращает значения из распределения скрытого режима, если BetaSim,sigma2Sim,RegimeSim]
= simulate(___)Mdl является байесовской линейной регрессионной моделью для выбора переменной стохастического поиска (SSVS), то есть, если Mdl является mixconjugateblm или mixsemiconjugateblm объект модели.
simulate невозможно получить значения из improper distribution, то есть распределения, плотность которого не интегрируется в 1.
Если Mdl является empiricalblm объект модели, тогда вы не можете задать Beta или Sigma2. Вы не можете симулировать из условных апостериорных распределений с помощью эмпирического распределения.
Каждый раз, когда simulate необходимо оценить апостериорное распределение (для примера, когда Mdl представляет собой предшествующее распределение, и вы поставляете X и y) и апостериор аналитически прослеживается, simulate симулирует непосредственно из апостериорной. В противном случае, simulate прибегает к симуляции Монте-Карло, чтобы оценить апостериор. Для получения дополнительной информации см. Апостериорная оценка и вывод.
Если Mdl является апостериорной моделью соединений, тогда simulate моделирует данные из него по-разному по сравнению с тем, когда Mdl является предшествующей моделью соединений, и вы поставляете X и y. Поэтому, если вы задаете одно и то же случайное начальное значение и генерируете случайные значения обоими способами, то вы можете не получить одинаковые значения. Однако соответствующие эмпирические распределения, основанные на достаточном количестве рисунков, фактически эквивалентны.
Этот рисунок показывает, как simulate уменьшает выборку при помощи значений NumDraws, Thin, и BurnIn.
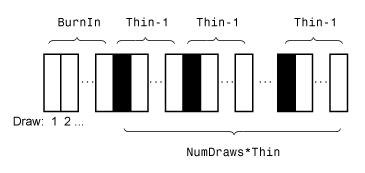
Прямоугольники представляют последовательные вытяжки из распределения. simulate удаляет белые прямоугольники из выборки. Оставшиеся NumDraws чёрные прямоугольники составляют выборку.
Если Mdl является semiconjugateblm объект модели, затем simulate выборки из апостериорного распределения путем применения пробоотборника Гиббса.
simulate использует значение по умолчанию Sigma2Start для σ2 и черпает значение β из π (β | σ2, X, y).
simulate рисует значение σ2 от π (σ2|<reservedrangesplaceholder3>,<reservedrangesplaceholder2>,<reservedrangesplaceholder1>) при помощи ранее сгенерированного значения β.
Функция повторяет шаги 1 и 2 до сходимости. Чтобы оценить сходимость, нарисуйте график трассировки выборки.
Если вы задаете BetaStart, затем simulate рисует значение σ2 от π (σ2|<reservedrangesplaceholder2>,<reservedrangesplaceholder1>,<reservedrangesplaceholder0> ) для запуска пробоотборника Гиббса.simulate не возвращает это сгенерированное значение σ2.
Если Mdl является empiricalblm объект модели, и вы не поставляете X и y, затем simulate черпает из Mdl.BetaDraws и Mdl.Sigma2Draws. Если NumDraws меньше или равно numel(Mdl.Sigma2Draws), затем simulate возвращает первое NumDraws элементы Mdl.BetaDraws и Mdl.Sigma2Draws как случайные рисунки для соответствующего параметра. В противном случае, simulate случайным образом повторяет NumDraws элементы из Mdl.BetaDraws и Mdl.Sigma2Draws.
Если Mdl является customblm объект модели, затем simulate использует дискретизатор MCMC, чтобы извлечь из апостериорного распределения. При каждой итерации программное обеспечение объединяет текущие значения коэффициентов регрессии и отклонения нарушения порядка в (Mdl.Intercept + Mdl.NumPredictors + 1) -by-1 вектор, и передает его в Mdl.LogPDF. Значение отклонения нарушения порядка является последним элементом этого вектора.
Для HMC-дискретизатора требуется как плотность журнала, так и его градиент. Градиент должен быть (NumPredictors+Intercept+1)-by-1 вектор. Если производные определенных параметров трудно вычислить, то в соответствующих местоположениях градиента задайте NaN вместо этого значения. simulate заменяет NaN значения с числовыми производными.
Если Mdl является lassoblm, mixconjugateblm, или mixsemiconjugateblm объект модели, и вы поставляете X и y, затем simulate выборки из апостериорного распределения путем применения пробоотборника Гиббса. Если вы не поставляете данные, то simulate выборки из аналитических, безусловных предварительных распределений.
simulate не возвращает начальные значения по умолчанию, которые она генерирует.
Если Mdl является mixconjugateblm или mixsemiconjugateblm, затем simulate сначала черпает из распределения режимов, учитывая текущее состояние цепи (значения RegimeStart, BetaStart, и Sigma2Start). Если вы рисуете одну выборку и не задаете значения для RegimeStart, BetaStart, и Sigma2Start, затем simulate использует значения по умолчанию и выдает предупреждение.
conjugateblm | customblm | diffuseblm | empiricalblm | lassoblm | mixconjugateblm | mixsemiconjugateblm | semiconjugateblm