Эмпирические, пользовательские и полунъюгатные предшествующие модели дают аналитически неразрешимые апостериорные распределения (для получения дополнительной информации см. «Аналитически неразрешимые апостериоры»). Чтобы суммировать апостериорное распределение для оценки и вывода, первая модель требует выборки Монте-Карло, в то время как две последние модели требуют выборки Марковской цепи Монте-Карло (MCMC). При оценке апостериоров с использованием выборки Монте-Карло, особенно выборки MCMC, можно столкнуться с проблемами, приводящими к выборкам, которые неадекватно представляют или не суммируют апостериорное распределение. В этом случае оценки и выводы, основанные на апостериорных рисунках, могут быть неправильными.
Даже если апостериор аналитически прослеживается или ваша выборка MCMC представляет истинную апостериорную скважину, ваш выбор предыдущего распределения может повлиять на апостериорное распределение нежелательными способами. Например, небольшое изменение предыдущего распределения, такое как небольшое увеличение значения предыдущего гиперпараметра, может оказывать большой эффект на апостериорные оценки или выводы. Если апостериор чувствителен к предшествующим предположениям, то интерпретации статистики и выводы, основанные на апостериоре, могут ввести в заблуждение.
Поэтому после получения апостериорного распределения из алгоритма дискретизации важно определить качество выборки. Кроме того, независимо от того, является ли апостериор аналитически отслеживаемым, важно проверить, насколько апостериор чувствителен к предшествующим допущениям распределения.
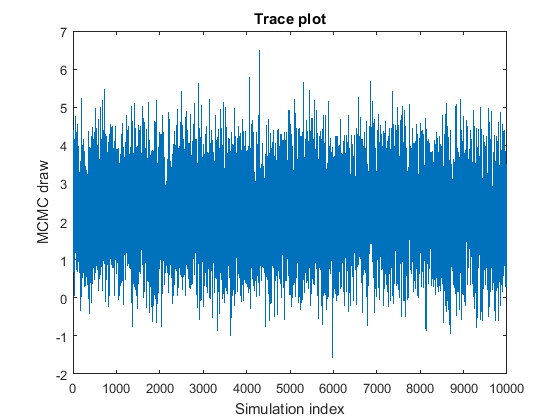
При построении выборки MCMC рекомендуется взять меньшую пилотную выборку, а затем просмотреть trace plots из нарисованных значений параметров, чтобы проверить, является ли выборка адекватной. Trace plots графики нарисованных значений параметров относительно индекса симуляции. Удовлетворительная выборка MCMC быстро достигает стационарного распределения и хорошо перемешивается, то есть исследует распределение широкими шагами, практически не запоминая предыдущего рисунка. Этот рисунок является примером удовлетворительной выборки MCMC.
Этот список описывает проблемные характеристики выборок MCMC, приводит пример того, что нужно искать на графике трассировки, и описывает, как решить проблему.
Выборка MCMC, по-видимому, перемещается к стационарному распределению, то есть отображается transient behavior.
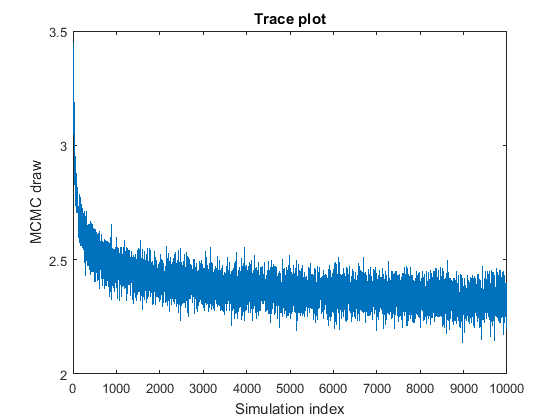
Чтобы устранить проблему, используйте один из следующих методов:
Задайте начальные значения для параметров, которые ближе к среднему значению стационарного распределения, или задайте значение, которое вы ожидаете в апостериоре, используя BetaStart и Sigma2Start Аргументы пары "имя-значение".
Задайте период burn-in, то есть число рисует начиная с начала, чтобы удалить из апостериорной оценки, используя BurnIn аргумент пары "имя-значение". Период горения должен быть достаточно большим, чтобы оставшийся образец напоминал удовлетворительный образец MCMC и достаточно маленьким, чтобы скорректированный размер выборки был достаточно большим.
MCMC выборка отображений высокую последовательную корреляцию. Следующие рисунки являются графиками трассировки и графиками автокорреляционной функции (ACF) (см. autocorr).
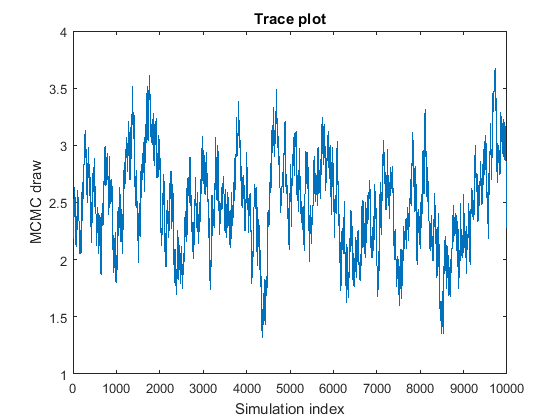
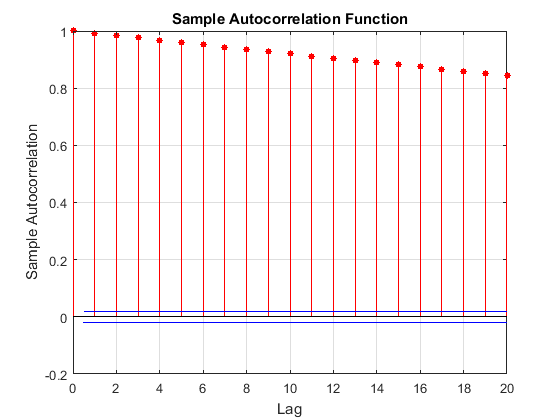
График трассировки показывает, что последующие выборки, по-видимому, являются функцией прошлых выборок. График ACF указывает на процесс с высокой автокорреляцией.
Такие выборки MCMC смешиваются плохо и занимают много времени, чтобы в достаточной степени исследовать распределение. Попробуйте следующее:
Если у вас достаточно ресурсов, то оценки, основанные на больших выборках MCMC, примерно верны.
Чтобы уменьшить высокую автокорреляцию, можно сохранить часть выборки MCMC, thinning используя Thin аргумент пары "имя-значение".
Для пользовательских предыдущих моделей попробуйте другой семплер при помощи 'Sampler' аргумент пары "имя-значение". Чтобы настроить параметры настройки сэмплера, создайте структуру опций сэмплера вместо этого с помощью sampleroptions, что позволяет вам задать дискретизатор и значения для его параметров настройки. Затем передайте структуру опций дискретизатора в estimate, simulate, или forecast при помощи 'Options' аргумент пары "имя-значение".
Выборка MCMC перескакивает из состояния в состояние.
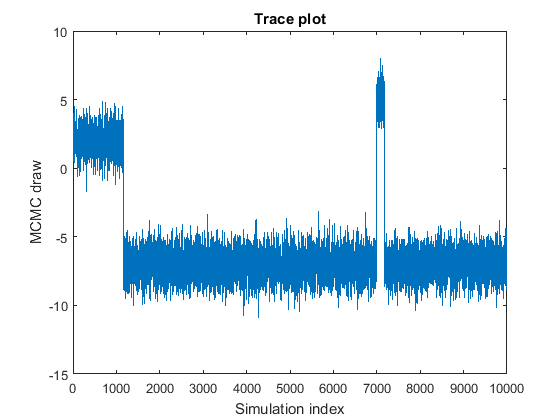
На графике показаны подвыборки с центром от значений 2, –7, и 5, которые хорошо перемешиваются. Это поведение может указывать на одно из следующих качеств:
По крайней мере, один из параметров не идентифицируется. Возможно, вам придется реформировать свою модель и предположения.
Могут быть проблемы с кодированием с вашим семплером Гиббса.
Стационарное распределение мультимодальное. В этом примере вероятность нахождения в состоянии с центром –7 является самым высоким, далее следуют 2и затем 5. Вероятность выхода из состояния с центром 7 низкая.
Если ваш предыдущий сильный, а размер выборки небольшой, тогда вы можете увидеть этот тип выборки MCMC, что не обязательно проблематично.
Марковская цепь не сходится к своему стационарному распределению.
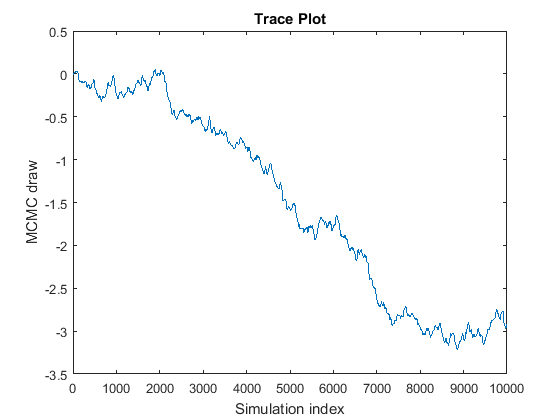
Кривая выглядит как случайная прогулка, потому что MCMC медленно исследует апостериор. Если возникает эта проблема, то апостериорные оценки, основанные на выборке MCMC, неправильны. Чтобы устранить проблему, попробуйте следующие методы:
Если у вас достаточно ресурсов, нарисуйте еще много выборки, а затем определите, оседает ли цепь и незначительно смешивается ли она. Если он оседает и относительно хорошо перемешивается, то удалите начальный фрагмент выборки и рассмотрите утончение остальной части выборки. Например, предположим, что вы рисуете 20000 выборки цепи на рисунке, а затем вы обнаруживаете, что цепь оседает вокруг -3 после 7000 рисует. Можно лечить ничьи 1:7000 как burn-in (BurnIn), а затем тонкий (Thin) остальные рисуют, чтобы достичь удовлетворительного уровня автокорреляции.
Репараметризовать предшествующее распределение. При оценке customblm объекты модели, можно задать репараметризацию отклонения нарушения порядка к шкале журнала с помощью Reparameterize аргумент пары "имя-значение".
Для пользовательских предыдущих моделей попробуйте другой семплер при помощи 'Sampler' аргумент пары "имя-значение". Чтобы настроить параметры настройки сэмплера, создайте структуру опций сэмплера вместо этого с помощью sampleroptions, что позволяет вам задать дискретизатор и значения для его параметров настройки. Затем передайте структуру опций дискретизатора в estimate, simulate, или forecast при помощи 'Options' аргумент пары "имя-значение".
В дополнение к графикам трассировки и ACF, estimate, simulate, и forecast оцените effective sample size. Если эффективный размер выборки составляет менее 1% от количества наблюдений, то эти функции выдают предупреждения. Для получения дополнительной информации см. раздел [1].
A sensitivity analysis включает определение того, насколько устойчивы апостериорные оценки к предшествующим и предположениям о распределении данных. То есть цель состоит в том, чтобы узнать, как замена начальных значений и предыдущих предположений разумными альтернативами влияет на апостериорное распределение и выводы. Если апостериорные и положительные значения не сильно варьируются по отношению к приложению, то апостериорные значения устойчивы к предшествующим предположениям и начальным значениям. Апостериоры и выводы, которые действительно варьируются в существенной степени с различными начальными предположениями, могут привести к неправильным интерпретациям.
Чтобы выполнить анализ чувствительности:
Идентифицируйте набор разумных предыдущих моделей. Включите диффузный (diffuseblm) модели и субъективные (conjugateblm или semiconjugateblm) модели, которые легче интерпретировать и разрешить включение предыдущей информации.
Для каждой из предыдущих моделей определите набор допустимых значений гиперзначений параметров. Например, для нормально-обратно-гамма-сопряженных или полуконъюгатных предшествующих моделей, выберите различные значения для предшествующей средней и ковариационной матрицы коэффициентов регрессии и формы и масштабных параметров обратного гамма-распределения дисперсии возмущения. Для получения дополнительной информации смотрите Mu, V, A, и B Аргументы пары "имя-значение" из bayeslm.
Для всех предыдущих допущений модели:
Сравните оценки и выводы среди моделей.
Если все оценки и выводы достаточно похожи, то апостериор является устойчивым.
Если оценки или выводы достаточно различны, тогда может возникнуть некоторая базовая проблема с выбранными априорными данными или вероятностью данных. Поскольку байесовская линейная регрессионая среда в Econometrics Toolbox™ всегда принимает, что данные Гауссовы, рассмотрим:
Добавление или удаление переменных предиктора из регрессионной модели
Делая априорные функции более информативными
Совершенно другие предыдущие допущения
Для получения дополнительной информации об анализе чувствительности см. [2], гл. 6.
[1] Гейер, К. Дж. Практическая марковская цепь Монте-Карло. Статистическая наука. Том 7, 1992, стр. 473-483.
[2] Гельман, А., Дж. Б. Карлин, Х. С. Стерн и Д. Б. Рубин. Байесовский анализ данных, 2-е. Эд. Бока Ратон, FL: Chapman & Hall/CRC, 2004.
estimate | forecast | simulate