Построение линейных инвариантных моделей времени

Программное обеспечение Model Predictive Control Toolbox™ поддерживает те же форматы модели LTI, что и программное обеспечение Control System Toolbox™. Вы можете использовать то, что наиболее удобно для вашего приложения, и преобразовать из одного формата в другой. Для получения дополнительной информации см. «Основные модели».

Модели передаточных функций

Передаточная функция (TF) связывает конкретную пару вход/выход. Для примера, если u (t) является объектом входа а y (t) является выход, передаточная функция, связывающая их, может быть:

$\frac{Y (s)}{U (s)} = G (s) = \frac{s + 2}{s^{2} + s + 10} e^{- 1.5 s}$

Этот TF состоит из numerator полинома, s + 2, многочлена знаменателя, s²+ s + 10, и задержка, которая 1,5 время модулей здесь. Определить G можно с помощью Control System Toolboxtf функция:

Gtf1 = tf([1 2], [1 1 10],'OutputDelay',1.5)

Transfer function:
                 s + 2
exp(-1.5*s) * ------------
              s^2 + s + 10

Модели нули/полюса/усиления

Как и формат TF, формат ноль/полюс/усиление (ZPK) связывает пару вход/выход. Различие, что числитель ZPK и полиномов знаменателя факторизированы, как в

$G (s) = 2.5 \frac{s + 0.45}{(s + 0.3) (s + 0.1 + 0.7 i) (s + 0.1 - 0.7 i)}$

(нули и/или полюсы являются комплексными числами в целом).

Вы задаете модель ZPK, задавая нули (нули ) (ы), полюс (ы) и усиление как в

poles = [-0.3, -0.1+0.7*i, -0.1-0.7*i];
Gzpk1 = zpk(-0.45,poles,2.5);

Модели в пространстве состояний

Формат в пространстве состояний удобен, если ваша модель является набором дифференциальных и алгебраических уравнений LTI. Например, рассмотрим следующую линеаризированную модель непрерывного реактора с мешалкой (CSTR), включающую экзотермическую (теплогенерирующую) реакцию [1].

$\frac{d {C^{'}}_{A}}{d t} = a_{11} {C^{'}}_{A} + a_{12} T^{'} + b_{11} {T^{'}}_{c} + b_{12} {C^{'}}_{A i}$

$\frac{d T^{'}}{d t} = a_{21} {C^{'}}_{A} + a_{22} T^{'} + b_{21} {T^{'}}_{c} + b_{22} {C^{'}}_{A i}$

где _CA - концентрация ключевого реагента, T - температура в реакторе, _Tc - температура хладагента, _CAi - концентрация реагента в сырье реактора и _aij и _bij являются постоянными. См. технологическую схему в CSTR Schematic. Простые числа (например, C _′ A) обозначают отклонение от номинального установившегося условия, при котором модель была линеаризирована.

Схема CSTR

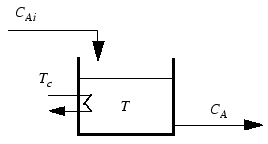
Измерение концентраций реагентов часто является трудным, если не невозможным. Предположим, что T является измеренным выходом, _CA является неизмеренным выходом, _Tc является манипулированной переменной и _CAi является неизмеренным нарушением порядка.

Модель подходит к общему формату пространства состояний

$\frac{d x}{d t} = A x + B u$

$y = C x + D u$

где

$x = [\begin{matrix} {C^{'}}_{A} \\ T^{'} \end{matrix}], u = [\begin{matrix} {T^{'}}_{c} \\ {C^{'}}_{A i} \end{matrix}], y = [\begin{matrix} T^{'} \\ {C^{'}}_{A} \end{matrix}]$

$A = [\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}], B = [\begin{matrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{matrix}], C = [\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}], D = [\begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix}]$

Следующий код показывает, как задать такую модель для некоторых определенных значений констант _aij и _bij:

A = [-0.0285  -0.0014
     -0.0371  -0.1476];
B = [-0.0850   0.0238
      0.0802   0.4462];
C = [0 1
     1 0];
D = zeros(2,2);
CSTR = ss(A,B,C,D);

Это задает модель пространства состояний в непрерывном времени. Если вы не задаете период выборки, применяется значение выборки по умолчанию, равное нулю. Можно также задать модели пространства состояний в дискретном времени. Можно задать задержки как в модели непрерывного времени, так и в модели дискретного времени.

Примечание

В примере CSTR матрица D равна нулю, и выход не реагирует мгновенно на изменение входа. Программное обеспечение Model Predictive Control Toolbox запрещает прямое (мгновенное) сквозное соединение от манипулируемой переменной до выхода. Например, модель CSTR может включать прямое сквозное соединение сигнала от неизмеренного нарушения порядка, _CAi, к _CA или T, но прямое сквозное соединение сигнала от _Tc к любому выходу будет нарушать это ограничение. Если модель имела прямое сквозное соединение от _Tc, можно добавить небольшую задержку на этом входе, чтобы обойти задачу.

Свойства объекта LTI

ss функция в последней линии вышеуказанного кода создает модель пространства состояний, CSTR, который является объектом LTI. tf и zpk команды Передаточной функции описанные в Модели и Zero/Pole/Gain Моделей также создают объекты LTI. Такие объекты содержат параметры модели, а также дополнительные свойства.

Свойства LTI для примера CSTR

Следующий код устанавливает некоторые из CSTR необязательные свойства модели:

CSTR.InputName = {'T_c','C_A_i'};
CSTR.OutputName = {'T','C_A'};
CSTR.StateName = {'C_A','T'};
CSTR.InputGroup.MV = 1;
CSTR.InputGroup.UD = 2;
CSTR.OutputGroup.MO = 1;
CSTR.OutputGroup.UO = 2;
CSTR

Первые три линии задают метки для переменных входа, вывода и состояния. Следующие четыре определяют тип сигнала для каждого входа и выхода. Обозначения MV, UD, MO, и UO средняя манипулируемая переменная, неизмеренное нарушение порядка, измеренный выход и неизмеренный выход. (Определения см. в разделе «Типы сигналов».) Для примера код задает, что вход 2 модели CSTR является неизмеренным нарушением порядка. Последняя линия приводит к отображению объекта LTI, генерируя следующие линии в MATLAB^® Командное окно:

A = 
            C_A        T
   C_A  -0.0285  -0.0014
   T    -0.0371  -0.1476
 
B = 
           T_c    C_Ai
   C_A  -0.085  0.0238
   T    0.0802  0.4462

C = 
        C_A    T
   T      0    1
   C_A    1    0
 
 
D = 
         T_c  C_Ai
   T       0     0
   C_A     0     0
 
Input groups:       
    Name    Channels
     MV        1    
     UD        2    
                    
Output groups:      
    Name    Channels
     MO        1    
     UO        2    
                    
Continuous-time model

Входные и выходные имена

Необязательный InputName и OutputName свойства влияют на отображения модели, как в приведенном выше примере. Программное обеспечение также использует InputName и OutputName свойства для маркировки графиков и таблиц. В этом контексте символ подчеркивания вызывает отображение следующего символа в виде индекса.

Входные и выходные типы

Общий случай. Как упоминалось в Signal Types, программное обеспечение Model Predictive Control Toolbox поддерживает три типа входа и два типа выхода. В проекте Model Predictive Control Toolbox обозначение входного и выходного типов определяет размерности контроллера и имеет другие важные последствия.

Например, предположим, что структура объекта была следующей:

Входные параметры объекта	Выходы объекта
Две манипулированные переменные (MVs)	Три измеренных выхода (MO)
Одно измеренное нарушение порядка (MD)	Два неизмеренных выхода (UO)
Два неизмеренных нарушения порядка (UD)

Получившийся контроллер имеет четыре входа (три MO и MD) и два выхода (MV). Это включает компенсацию с feedforward для измеренного нарушения порядка и принимает, что вы хотели включить неизмеренные нарушения порядка и выходы в проект регулятора.

Если вы не хотите, чтобы конкретный сигнал рассматривался как один из вышеуказанных типов, можно сделать одно из следующих:

Удалите сигнал перед использованием модели в проектировании контроллера.
Для выхода обозначите его как unmeasured, затем установите его вес равным нулю.
Для входов определите его как неизмеренное нарушение порядка, а затем задайте пользовательскую оценку состояния, которая игнорирует входы.
Примечание
По умолчанию программное обеспечение принимает, что неопределенные входы объекта управления являются манипулируемыми переменными, и неопределенные выходы измеряются. Таким образом, если бы вы не задали типы сигналов в приведенном выше примере, контроллер имел бы четыре входа (при условии, что все выходы объекта были измерены) и пять выходы (при условии, что все входы объекта были управляемыми переменными).

Для CSTR модели, допущения Model Predictive Control Toolbox по умолчанию неправильны. Вы должны задать его InputGroup и OutputGroup свойства, как показано в приведенном выше коде, или изменение настроек по умолчанию при загрузке модели в MPC Designer.

Использовать setmpcsignals для создания определения типа. Для примера:

CSTR = setmpcsignals(CSTR,'UD',2,'UO',2);

устанавливает InputGroup и OutputGroup к тем же значениям, что и в предыдущем примере. The CSTR отображение будет включать следующие линии:

Input groups:              
       Name        Channels
    Unmeasured        2    
    Manipulated       1    
                           


Output groups:             
       Name       Channels 
    Unmeasured       2     
     Measured        1

Заметьте, что setmpcsignals устанавливает незаданные входы в Manipulated и неопределенные выходы для Measured.

Характеристики модели LTI

Программное обеспечение Control System Toolbox обеспечивает функции для анализа моделей LTI. Некоторые из наиболее часто используемых перечислены ниже. Введите код примера в подсказке MATLAB, чтобы увидеть, как они работают для CSTR пример.

Пример	Предполагаемый результат
`dcgain(CSTR)`	Вычислите матрицу усиления для `CSTR` входные/выходные пары модели.
`impulse(CSTR)`	Графическое `CSTR` модульно-импульсная характеристика модели.
`linearSystemAnalyzer(CSTR)`	Откройте Linear System Analyzer с `CSTR` модель загружена. Затем можно отобразить характеристики модели путем выбора меню.
`pole(CSTR)`	Вычислите `CSTR` полюса модели (для проверки устойчивости и т.д.).
`step(CSTR)`	Графическое `CSTR` эталонная характеристика модели.
`zero(CSTR)`	Вычислите `CSTR` нули трансмиссии модели.

Ссылки

[1] Себорг, Д. Э., Т. Ф. Эдгар, и Д. А. Mellichamp, Process Dynamics and Control, 2nd Edition, Wiley, 2004, pp. 34-36 и 94-95.

См. также

setmpcsignals | ss | tf | zpk

Документация