Документация

pdeplot(model,'XYData',results.NodalSolution) строит графики решения model в узловых местоположениях в качестве цветной объемной поверхностной диаграммы с помощью 'jet' по умолчанию палитра.

pdeplot(model,'XYData',results.Temperature,'ColorMap','hot') строит графики температуры в узловых местоположениях для 2-D модели теплового анализа. Этот синтаксис создает цветную объемную поверхностную диаграмму с помощью 'hot' палитра.

pdeplot(model,'XYData',results.VonMisesStress,'Deformation',results.Displacement) строит графики напряжения фон Мизеса и показывает деформированную форму для 2-D модели структурного анализа.

pdeplot(model,'XYData',results.ModeShapes.ux) строит графики x-компонент модального смещения для 2-D модели структурного модального анализа.

pdeplot(model,'XYData',results.ElectricPotential) строит графики электрического потенциала в узловых местоположениях для 2-D модели электростатического анализа.

pdeplot(model) строит график mesh, указанной в model.

pdeplot(mesh) строит график mesh, заданный как Mesh свойство 2-D model объект типа PDEModel.

pdeplot(nodes,elements) строит графики mesh, заданные ее nodes и elements.

pdeplot(p,e,t) строит графики mesh, описанной p, e, и t.

pdeplot(___,Name,Value) строит график mesh, данных в узловых местоположениях или как mesh, так и данных, в зависимости от Name,Value аргументы в виде пар. Используйте любые аргументы из предыдущих синтаксисов.

Задайте по крайней мере один из FlowData (график векторного поля), XYData (график цветной поверхности), или ZData (3-D график высоты) пар имя-значение. В противном случае, pdeplot строит график mesh без данных. Можно объединить любое количество типов графиков.

Для тепловой модели можно построить график температуры или градиента температуры.
Для несущей модели можно построить график смещения, напряжения, деформации и напряжения фон Мизеса. В сложение можно показать деформированную форму и задать масштабный коэффициент для графика деформации.

h = pdeplot(___) возвращает указатель на график, используя любой из предыдущих синтаксисов.

Примеры

2-D Сетчатые графики

Создайте модель УЧП. Включите геометрию встроенной функции lshapeg. Создайте сетку геометрии и постройте график.

model = createpde;
geometryFromEdges(model,@lshapeg);
mesh = generateMesh(model);
pdeplot(model)

Figure contains an axes. The axes contains 2 objects of type line.

Также можно построить график mesh при помощи mesh как входной параметр.

pdeplot(mesh)

Figure contains an axes. The axes contains 2 objects of type line.

Другой подход состоит в том, чтобы использовать узлы и элементы mesh в качестве входных параметров для pdeplot.

pdeplot(mesh.Nodes,mesh.Elements)

Figure contains an axes. The axes contains an object of type line.

Отображение меток узлов. Использование xlim и ylim для масштабирования конкретных узлов.

pdeplot(model,'NodeLabels','on')
xlim([-0.2,0.2])
ylim([-0.2,0.2])

Figure contains an axes. The axes contains 2 objects of type line.

Отображение меток элемента.

pdeplot(model,'ElementLabels','on')
xlim([-0.2,0.2])
ylim([-0.2,0.2])

Figure contains an axes. The axes contains 2 objects of type line.

Графики решений

Создайте цветные 2-D и 3-D графики решения модели PDE.

Создайте модель УЧП. Включите геометрию встроенной функции lshapeg. Создайте сетку геометрии.

model = createpde;
geometryFromEdges(model,@lshapeg);
generateMesh(model);

Установите нулевые граничные условия Дирихле на всех ребрах.

applyBoundaryCondition(model,'dirichlet','Edge',1:model.Geometry.NumEdges,'u',0);

Задайте коэффициенты и решите УЧП.

specifyCoefficients(model,'m',0, ...
                          'd',0, ...
                          'c',1, ...
                          'a',0, ...
                          'f',1);
results = solvepde(model)

results = 
  StationaryResults with properties:

    NodalSolution: [1177x1 double]
       XGradients: [1177x1 double]
       YGradients: [1177x1 double]
       ZGradients: []
             Mesh: [1x1 FEMesh]

Доступ к решению в узловых местоположениях.

u = results.NodalSolution;

Постройте график 2-D решения.

pdeplot(model,'XYData',u)

Figure contains an axes. The axes contains an object of type patch.

Постройте график 3-D решения.

pdeplot(model,'XYData',u,'ZData',u)

Figure contains an axes. The axes contains an object of type patch.

График полей градиента решений

Постройте график градиента УЧП решения как график полей градиента.

Создайте модель УЧП. Включите геометрию встроенной функции lshapeg. Создайте сетку геометрии.

model = createpde;
geometryFromEdges(model,@lshapeg);
generateMesh(model);

Установите нулевые граничные условия Дирихле на всех ребрах.

applyBoundaryCondition(model,'dirichlet','Edge',1:model.Geometry.NumEdges,'u',0);

Задайте коэффициенты и решите УЧП.

specifyCoefficients(model,'m',0, ...
                          'd',0, ...
                          'c',1, ...
                          'a',0, ...
                          'f',1);
results = solvepde(model)

results = 
  StationaryResults with properties:

    NodalSolution: [1177x1 double]
       XGradients: [1177x1 double]
       YGradients: [1177x1 double]
       ZGradients: []
             Mesh: [1x1 FEMesh]

Доступ к градиенту решения в узловых местоположениях.

ux = results.XGradients;
uy = results.YGradients;

Постройте график градиента как график полей градиента.

pdeplot(model,'FlowData',[ux,uy])

Figure contains an axes. The axes contains an object of type quiver.

Составной график

Постройте график решения 2-D УЧП в 3-D с 'jet' раскраска и mesh, и включать график полей градиента. Получите указатели на объекты осей.

Создайте модель УЧП. Включите геометрию встроенной функции lshapeg. Создайте сетку геометрии.

model = createpde;
geometryFromEdges(model,@lshapeg);
generateMesh(model);

Установите нулевые граничные условия Дирихле на всех ребрах.

applyBoundaryCondition(model,'dirichlet','Edge',1:model.Geometry.NumEdges,'u',0);

Задайте коэффициенты и решите УЧП.

specifyCoefficients(model,'m',0, ...
                          'd',0, ...
                          'c',1, ...
                          'a',0, ...
                          'f',1);
results = solvepde(model)

results = 
  StationaryResults with properties:

    NodalSolution: [1177x1 double]
       XGradients: [1177x1 double]
       YGradients: [1177x1 double]
       ZGradients: []
             Mesh: [1x1 FEMesh]

Доступ к решению и его градиенту в узловых местоположениях.

u = results.NodalSolution;
ux = results.XGradients;
uy = results.YGradients;

Постройте график решения в 3-D с 'jet' раскраска и mesh, и включать градиент в качестве графика полей градиента.

h = pdeplot(model,'XYData',u,'ZData',u, ...
                  'FaceAlpha',0.5, ...
                  'FlowData',[ux,uy], ...
                  'ColorMap','jet', ...
                  'Mesh','on')

Figure contains an axes. The axes contains 2 objects of type patch, quiver.

h = 
  3x1 graphics array:

  Patch
  Quiver
  ColorBar

Решение для переходной тепловой модели

Решите 2-D переходную тепловую задачу.

Создайте переходную тепловую модель для этой задачи.

thermalmodel = createpde('thermal','transient');

Создайте геометрию и включите ее в модель.

SQ1 = [3; 4; 0; 3; 3; 0; 0; 0; 3; 3];
D1 = [2; 4; 0.5; 1.5; 2.5; 1.5; 1.5; 0.5; 1.5; 2.5];
gd = [SQ1 D1];
sf = 'SQ1+D1';
ns = char('SQ1','D1');
ns = ns';
dl = decsg(gd,sf,ns);
geometryFromEdges(thermalmodel,dl);
pdegplot(thermalmodel,'EdgeLabels','on','FaceLabels','on')
xlim([-1.5 4.5])
ylim([-0.5 3.5])
axis equal

Figure contains an axes. The axes contains 11 objects of type line, text.

Для квадратной области присвойте следующие тепловые свойства:

Теплопроводность $10 W / (m \cdot^{\circ} C)$
Массовая плотность составляет $2 kg / m^{3}$
Удельное тепло $0.1 J / ({kg \cdot}^{\circ} C)$

thermalProperties(thermalmodel,'ThermalConductivity',10, ...
                               'MassDensity',2, ...
                               'SpecificHeat',0.1, ...
                               'Face',1);

Для алмазной области присвойте следующие тепловые свойства:

Теплопроводность $2 W / (m \cdot^{\circ} C)$
Массовая плотность составляет $1 kg / m^{3}$
Удельное тепло $0.1 J / ({kg \cdot}^{\circ} C)$

thermalProperties(thermalmodel,'ThermalConductivity',2, ...
                               'MassDensity',1, ...
                               'SpecificHeat',0.1, ...
                               'Face',2);

Предположим, что алмазообразная область является источником тепла с плотностью $4 W / m^{2}$ .

internalHeatSource(thermalmodel,4,'Face',2);

Применить постоянную температуру $0^{\circ} C$ по сторонам квадратной пластины.

thermalBC(thermalmodel,'Temperature',0,'Edge',[1 2 7 8]);

Установите начальную температуру равной 0 ° C.

thermalIC(thermalmodel,0);

Сгенерируйте mesh.

generateMesh(thermalmodel);

Динамика для этой задачи очень быстрая. Температура достигает устойчивого состояния примерно за 0,1 секунды. Чтобы захватить интересную часть динамики, установите время решения на logspace(-2,-1,10). Эта команда возвращает 10 логарифмических интервалов времени решения между 0,01 и 0,1.

tlist = logspace(-2,-1,10);

Решить уравнение.

thermalresults = solve(thermalmodel,tlist)

thermalresults = 
  TransientThermalResults with properties:

      Temperature: [1481x10 double]
    SolutionTimes: [1x10 double]
       XGradients: [1481x10 double]
       YGradients: [1481x10 double]
       ZGradients: []
             Mesh: [1x1 FEMesh]

Постройте график решения с помощью изотермических линий с помощью контурного графика.

T = thermalresults.Temperature;
pdeplot(thermalmodel,'XYData',T(:,10),'Contour','on','ColorMap','hot')

Figure contains an axes. The axes contains 12 objects of type patch, line.

Построение графика деформированной формы для статической задачи плоскостной деформации

Создайте модель структурного анализа для статической задачи плоскостной деформации.

structuralmodel = createpde('structural','static-planestrain');

Создайте геометрию и включите ее в модель. Постройте график геометрии.

geometryFromEdges(structuralmodel,@squareg);
pdegplot(structuralmodel,'EdgeLabels','on')
axis equal

Figure contains an axes. The axes contains 5 objects of type line, text.

Задайте модуль Юнга и коэффициент Пуассона.

structuralProperties(structuralmodel,'PoissonsRatio',0.3, ...
                                     'YoungsModulus',210E3);

Задайте x-компонент принудительного перемещения для ребра 1.

structuralBC(structuralmodel,'XDisplacement',0.001,'Edge',1);

Задайте, что ребро 3 является фиксированным контуром.

structuralBC(structuralmodel,'Constraint','fixed','Edge',3);

Сгенерируйте mesh и решите проблему.

generateMesh(structuralmodel);
structuralresults = solve(structuralmodel);

Постройте график деформированной формы с помощью масштабного коэффициента по умолчанию. По умолчанию pdeplot внутренне определяет коэффициент шкалы на основе размерностей геометрии и величины деформации.

pdeplot(structuralmodel,'XYData',structuralresults.VonMisesStress, ...
                        'Deformation',structuralresults.Displacement, ...
                        'ColorMap','jet')

Figure contains an axes. The axes contains an object of type patch.

Постройте график деформированной формы с коэффициентом шкалы 500.

pdeplot(structuralmodel,'XYData',structuralresults.VonMisesStress, ...
                        'Deformation',structuralresults.Displacement, ...
                        'DeformationScaleFactor',500,...
                        'ColorMap','jet')

Figure contains an axes. The axes contains an object of type patch.

Построение графика деформированной формы без масштабирования.

pdeplot(structuralmodel,'XYData',structuralresults.VonMisesStress, ...
                        'ColorMap','jet')

Figure contains an axes. The axes contains an object of type patch.

Решение модальной структурной модели анализа

Найдите основной (самый низкий) режим 2-D консольного луча, принимая распространенность условия плоского напряжения.

Задайте следующие геометрические и структурные свойства балки вместе с модулем толщиной плоскости-напряжения.

length = 5;
height = 0.1;
E = 3E7;
nu = 0.3;
rho = 0.3/386;

Создайте модель плоскость-напряжение модели, присвойте геометрию и сгенерируйте mesh.

structuralmodel = createpde('structural','modal-planestress');
gdm = [3;4;0;length;length;0;0;0;height;height];
g = decsg(gdm,'S1',('S1')');
geometryFromEdges(structuralmodel,g);

Задайте максимальный размер элемента (пять элементов через толщину балки).

hmax = height/5;
msh=generateMesh(structuralmodel,'Hmax',hmax);

Задайте структурные свойства и граничные ограничения.

structuralProperties(structuralmodel,'YoungsModulus',E, ...
                                     'MassDensity',rho, ... 
                                     'PoissonsRatio',nu);
structuralBC(structuralmodel,'Edge',4,'Constraint','fixed');

Вычислите аналитическую основную частоту (Гц), используя теорию луча.

I = height^3/12;
analyticalOmega1 = 3.516*sqrt(E*I/(length^4*(rho*height)))/(2*pi)

analyticalOmega1 = 126.9498

Задайте частотную область значений, который включает аналитически вычисленную частоту и решите модель.

modalresults = solve(structuralmodel,'FrequencyRange',[0,1e6])

modalresults = 
  ModalStructuralResults with properties:

    NaturalFrequencies: [32x1 double]
            ModeShapes: [1x1 FEStruct]
                  Mesh: [1x1 FEMesh]

Решатель находит естественные частоты и значения модального смещения в узловых местоположениях. Для доступа к этим значениям используйте modalresults.NaturalFrequencies и modalresults.ModeShapes.

modalresults.NaturalFrequencies/(2*pi)

modalresults.ModeShapes

ans = 
  FEStruct with properties:

           ux: [6511x32 double]
           uy: [6511x32 double]
    Magnitude: [6511x32 double]

Постройте график y-составляющей решения для основной частоты.

pdeplot(structuralmodel,'XYData',modalresults.ModeShapes.uy(:,1))
title(['First Mode with Frequency ', ...
        num2str(modalresults.NaturalFrequencies(1)/(2*pi)),' Hz'])
axis equal

Figure contains an axes. The axes with title First Mode with Frequency 126.9416 Hz contains an object of type patch.

Решение электростатической модели анализа

Решите электромагнитную задачу и найдите электрический потенциал и распределение поля для 2-D геометрии, представляющей пластину с отверстием.

Создайте электромагнитную модель для электростатического анализа.

emagmodel = createpde('electromagnetic','electrostatic');

Импортируйте и постройте график геометрии, представляющей пластину с отверстием.

importGeometry(emagmodel,'PlateHolePlanar.stl');
pdegplot(emagmodel,'EdgeLabels','on')

Figure contains an axes. The axes contains an object of type line.

Задайте вакуумную диэлектрическую проницаемость в системе модулей СИ.

emagmodel.VacuumPermittivity = 8.8541878128E-12;

Задайте относительную диэлектрическую проницаемость материала.

electromagneticProperties(emagmodel,'RelativePermittivity',1);

Примените условия контура напряжения к ребрам, обрамляющему прямоугольник и круг.

electromagneticBC(emagmodel,'Voltage',0,'Edge',1:4);
electromagneticBC(emagmodel,'Voltage',1000,'Edge',5);

Задайте плотность заряда для всей геометрии.

electromagneticSource(emagmodel,'ChargeDensity',5E-9);

Сгенерируйте mesh.

generateMesh(emagmodel);

Решить модель.

R = solve(emagmodel)

R = 
  ElectrostaticResults with properties:

      ElectricPotential: [1218x1 double]
          ElectricField: [1x1 FEStruct]
    ElectricFluxDensity: [1x1 FEStruct]
                   Mesh: [1x1 FEMesh]

Постройте график электрического потенциала и поля.

pdeplot(emagmodel,'XYData',R.ElectricPotential, ...
                  'FlowData',[R.ElectricField.Ex ...
                              R.ElectricField.Ey])
axis equal

Figure contains an axes. The axes contains 2 objects of type patch, quiver.

[p, e, t] Сетчатые графики и графики решений

Постройте график p,e,t mesh. Отобразите решение с помощью 2-D и 3-D цветных графиков.

Создайте геометрию, mesh, граничные условия, коэффициенты УЧП и решение.

[p,e,t] = initmesh('lshapeg');
u = assempde('lshapeb',p,e,t,1,0,1);

Постройте график mesh.

pdeplot(p,e,t)

Figure contains an axes. The axes contains 2 objects of type line.

Постройте график решения как 2-D цветной график.

pdeplot(p,e,t,'XYData',u)

Figure contains an axes. The axes contains an object of type patch.

Постройте график решения как 3-D цветной график.

pdeplot(p,e,t,'XYData',u,'ZData',u)

Figure contains an axes. The axes contains an object of type patch.

Входные параметры

`model` - Объект модели
`PDEModel` | объекта `ThermalModel` | объекта `StructuralModel` | объекта `ElectromagneticModel` объект

Объект модели, заданный как PDEModel объект, ThermalModel объект, StructuralModel объект, или ElectromagneticModel объект.

Пример: model = createpde(1)

Пример: thermalmodel = createpde('thermal','steadystate')

Пример: structuralmodel = createpde('structural','static-solid')

Пример: emagmodel = createpde('electromagnetic','magnetostatic')

`mesh` - Объект Mesh
`Mesh` свойство `PDEModel` объект | выход `generateMesh`

Объект Mesh, заданный как Mesh свойство PDEModel объект или как выход generateMesh.

Пример: model.Mesh

`nodes` - Узловые координаты
2-by- NumNodes матрица

Узловые координаты, заданные как матрица 2 байта NumNodes. NumNodes является числом узлов.

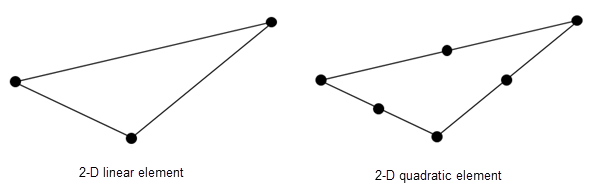
`elements` - Матрица связности элемента в терминах идентификаторов узла
3-by- NumElements матрица | 6-by- NumElements матрица

Матрица связности элемента в терминах идентификаторов узла, заданная как матрица 3 байта NumElements или 6 байтов NumElements. Линейные сетки содержат только угловые узлы. Для линейных сетей матрица связности имеет три узла на 2-D элемент. Квадратичные сетки содержат угловые узлы и узлы в середине каждого ребра элемента. Для квадратичных сетей матрица связности имеет шесть узлов на 2-D элемент.

`p` - Mesh
матрица

Mesh точки, заданные как 2-бай- Np матрица точек, где Np - число точек в mesh. Описание (p, e, t) матрицы, см. Данные сетки как [p, e, t] Тройки.

Как правило, вы используете p, e, и t данные экспортированы из приложения PDE Modeler или сгенерированы initmesh или refinemesh.

Пример: [p,e,t] = initmesh(gd)

Типы данных: double

`e` - Кромки сетки
матрица

Сетка ребер, заданная как 7-by- Ne матрица ребер, где Ne - количество ребер в mesh. Описание (p, e, t) матрицы, см. Данные сетки как [p, e, t] Тройки.

Пример: [p,e,t] = initmesh(gd)

Типы данных: double

`t` - Сетчатые треугольники
матрица

Сетка треугольников, заданная как 4-by- Nt матрица треугольников, где Nt - количество треугольников в mesh. Описание (p, e, t) матрицы, см. Данные сетки как [p, e, t] Тройки.

Пример: [p,e,t] = initmesh(gd)

Типы данных: double

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

Пример: pdeplot(model,'XYData',u,'ZData',u)

Когда вы используете PDEModel объект, pdeplot(model,'XYData',u,'ZData',u) устанавливает раскраску объемной поверхностной диаграммы в решение u, и устанавливает высоты для 3-D графика равными u. Вот u является NodalSolution свойство результатов УЧП, возвращаемое solvepde или solvepdeeig.

Когда вы используете [p,e,t] представление, pdeplot(p,e,t,'XYData',u,'ZData',u) устанавливает раскраску объемной поверхностной диаграммы в решение u и устанавливает высоты для 3-D графика в решение u. Вот u является решением, возвращенным устаревшим решателем, таким как assempde.

Совет

Графики данных

`'XYData'` - Данные цветной объемной поверхностной диаграммы
вектор

Данные цветной объемной поверхностной диаграммы, заданные как разделенная разделенными запятой парами, состоящая из 'XYData' и вектор. Если вы используете [p,e,t] представление, задайте данные для точек в векторе длины size(p,2), или задайте данные для треугольников в векторе длины size(t,2).

Как правило, вы задаете XYData к решению u. pdeplot функция использует XYData для раскраски как 2-D, так и 3-D графиков.
pdeplot использует палитру, заданную в ColorMap Пара "имя-значение", используя стиль, заданный в XYStyle Пара "имя-значение".
Когда Contour Пара "имя-значение" 'on', pdeplot также строит графики кривых уровня XYData.
pdeplot строит графики реальной части комплексных данных.

Чтобы построить график kкомпонент решения системы PDE, извлеките соответствующую часть решения. Для примера при использовании PDEModel объект, задайте:

results = solvepde(model);
u = results.NodalSolution; % each column of u has one component of u
pdeplot(model,'XYData',u(:,k)) % data for column k

При использовании [p,e,t] представление, задайте:

np = size(p,2); % number of node points
uk = reshape(u,np,[]); % each uk column has one component of u
pdeplot(p,e,t,'XYData',uk(:,k)) % data for column k

Пример: 'XYData',u

Типы данных: double

`'XYStyle'` - Выбор окраски
`'interp'` (по умолчанию) | `'off'` | `'flat'`

Выбор раскраски, заданный как разделенная разделенными запятой парами, состоящая из 'XYStyle' и 'interp', 'off', или 'flat'.

'off' - Нет затенения, отображается только сетка.
'flat' - Каждый треугольник в mesh имеет равномерный цвет.
'interp' - Окрашивание графика плавно интерполируется.

Выбор раскраски относится к XYData Пара "имя-значение".

Пример: 'XYStyle','flat'

Типы данных: char | string

`'ZData'` - Данные для 3-D высот графиков
матрица

Данные для 3-D высот графиков, заданные как разделенная разделенными запятой парами, состоящая из 'ZData' и матрицу. Если вы используете [p,e,t] представление, предоставляйте данные для точек в векторе длины size(p,2) или данные для треугольников в векторе длины size(t,2).

Как правило, вы задаете ZData на u, решение. The XYData пара "имя-значение" устанавливает раскраску 3-D графика.
The ZStyle Пара "имя-значение" определяет, является ли график непрерывным или прерывистым.
pdeplot строит графики реальной части комплексных данных.

results = solvepde(model);
u = results.NodalSolution; % each column of u has one component of u
pdeplot(model,'XYData',u(:,k),'ZData',u(:,k)) % data for column k

При использовании [p,e,t] представление, задайте:

np = size(p,2); % number of node points
uk = reshape(u,np,[]); % each uk column has one component of u
pdeplot(p,e,t,'XYData',uk(:,k),'ZData',uk(:,k)) % data for column k

Пример: 'ZData',u

Типы данных: double

`'ZStyle'` - 3-D стиль графика
`'continuous'` (по умолчанию) | `'off'` | `'discontinuous'`

3-D графики стиль, заданный как разделенная запятой пара, состоящий из 'ZStyle' и одно из следующих значений:

'off' - Нет 3-D графика.
'discontinuous' - Каждый треугольник в mesh имеет равномерную высоту на 3-D графике.
'continuous' - график 3-D поверхности непрерывен.

Если вы используете ZStyle не задавая ZData Пара "имя-значение", затем pdeplot игнорирует ZStyle.

Пример: 'ZStyle','discontinuous'

Типы данных: char | string

`'FlowData'` - Данные для квивер-графика
матрица

Данные для графика полей градиента, заданные как разделенная запятой пара, состоящая из 'FlowData' и M-by- 2 матрица, где M количество узлов сетки. FlowData содержит x и y значения поля в точках mesh.

Когда вы используете PDEModel объект, задать FlowData следующим образом:

results = solvepde(model);
gradx = results.XGradients;
grady = results.YGradients;
pdeplot(model,'FlowData',[gradx grady])

Когда вы используете [p,e,t] представление, задание FlowData следующим образом:

[gradx,grady] = pdegrad(p,t,u); % Calculate gradient
pdeplot(p,e,t,'FlowData',[gradx;grady])

Когда вы используете ZData чтобы представлять 2-D УЧП решение как 3-D график, и вы также включите график полей градиента, график полей градиента появляется в плоскости z = 0.

pdeplot строит графики реальной части комплексных данных.

Пример: 'FlowData',[ux uy]

Типы данных: double

`'FlowStyle'` - Индикатор для отображения квивер-графика
`'arrow'` (по умолчанию) | `'off'`

Индикатор для отображения графика полей градиента, заданный как разделенная запятой пара, состоящий из 'FlowStyle' и 'arrow' или 'off'. Здесь, 'arrow' отображает график полей градиента, заданный как FlowData Пара "имя-значение".

Пример: 'FlowStyle','off'

Типы данных: char | string

`'XYGrid'` - Индикатор для преобразования данных сетки в x - y сетку
`'off'` (по умолчанию) | `'on'`

Индикатор для преобразования данных сетки в сетку x - y перед графическим изображением, заданный как разделенная разделенными запятой парами, состоящая из 'XYGrid' и 'off' или 'on'.

Примечание

Это преобразование может изменить геометрию и уменьшить качество графика.

По умолчанию сетка имеет около sqrt(size(t,2)) элементы в каждом направлении.

Пример: 'XYGrid','on'

Типы данных: char | string

`'GridParam'` - Индивидуальные x - y сетка
`[tn;a2;a3]` из более раннего вызова в `tri2grid`

Настраиваемая x - y сетка, заданная как разделенная разделенными запятой парами, состоящая из 'GridParam' и матричный [tn;a2;a3]. Для примера:

[~,tn,a2,a3] = tri2grid(p,t,u,x,y);
pdeplot(p,e,t,'XYGrid','on','GridParam',[tn;a2;a3],'XYData',u)

Для получения дополнительной информации о данных сетки и ее x и y аргументы, см. tri2grid. tri2grid функция не работает со PDEModel объекты.

Пример: 'GridParam',[tn;a2;a3]

Типы данных: double

Сетчатые графики

`'NodeLabels'` - Метки узлов
`'off'` (по умолчанию) | `'on'`

Метки узла, заданные как разделенная разделенными запятой парами, состоящая из 'NodeLabels' и 'off' или 'on'.

pdeplot игнорирует NodeLabels когда вы используете его с ZData.

Пример: 'NodeLabels','on'

Типы данных: char | string

`'ElementLabels'` - Метки элемента
`'off'` (по умолчанию) | `'on'`

Метки элемента, заданные как разделенная разделенными запятой парами, состоящая из 'ElementLabels' и 'off' или 'on'.

pdeplot игнорирует ElementLabels когда вы используете его с ZData.

Пример: 'ElementLabels','on'

Типы данных: char | string

Структурные Графики для анализа

`'Deformation'` - Данные для графического изображения деформированной формы
`Displacement` свойство `StaticStructuralResults` объект

Данные для графического изображения деформированной формы для модели структурного анализа, заданные как разделенная разделенными запятой парами, состоящая из 'Deformation' и Displacement свойство StaticStructuralResults объект.

В недеформированной форме центральные узлы в квадратичных сетках всегда складываются на половинном расстоянии между углами. При построении графика деформированной формы центральные узлы могут отойти от центра ребра.

Пример: 'Deformation',structuralresults.Displacement

`'DeformationScaleFactor'` - Масштабный коэффициент для графического изображения деформированной формы
вещественное число

Масштабный коэффициент для графического изображения деформированной формы, заданный как разделенная разделенными запятой парами, состоящая из 'DeformationScaleFactor' и действительное число. Используйте этот аргумент с Deformation Пара "имя-значение". Значение по умолчанию задается внутренне, основываясь на размерностях геометрии и величине деформации.

Пример: 'DeformationScaleFactor',100

Типы данных: double

Аннотации и внешний вид

`'ColorBar'` - Индикатор для включения цветовой панели
`'on'` (по умолчанию) | `'off'`

Индикатор для включения цветовой панели в виде разделенной разделенными запятой парами, состоящей из 'ColorBar' и 'on' или 'off'. Задайте 'on' отображение полосы с указанием числовых значений цветов на графике. Для получения дополнительной информации см. colorbar. The pdeplot функция использует палитру, заданную в ColorMap Пара "имя-значение".

Пример: 'ColorBar','off'

Типы данных: char | string

`'ColorMap'` - Палитра
`'cool'` (по умолчанию) | `ColorMap` значение или матрица таких значений

Палитра, заданная как разделенная разделенными запятой парами, состоящая из 'ColorMap' и значение, представляющее встроенную палитру или матрицу палитры. Для получения дополнительной информации см. colormap.

ColorMap должен использоваться с XYData Пара "имя-значение".

Пример: 'ColorMap','jet'

Типы данных: double | char | string

`'Mesh'` - Индикатор для отображения mesh
`'off'` (по умолчанию) | `'on'`

Индикатор для отображения mesh, заданный как разделенная разделенными запятой парами, состоящая из 'Mesh' и 'on' или 'off'. Задайте 'on' отображение mesh на графике.

Пример: 'Mesh','on'

Типы данных: char | string

`'Title'` - Заголовок графика
вектор символов

Заголовок графика, заданное как разделенная разделенными запятой парами, состоящая из 'Title' и вектор символов.

Пример: 'Title','Solution Plot'

Типы данных: char | string

`'FaceAlpha'` - Поверхностная прозрачность для 3-D геометрии
`1` (по умолчанию) | вещественный номер из `0` через `1`

Поверхностная прозрачность для 3-D геометрии, заданная как разделенная разделенными запятой парами, состоящая из 'FaceAlpha' и действительное число из 0 через 1. Значение по умолчанию 1 указывает на отсутствие прозрачности. Значение 0 указывает на полную прозрачность.

Пример: 'FaceAlpha',0.5

Типы данных: double

`'Contour'` - Индикатор для построения кривых уровня
`'off'` (по умолчанию) | `'on'`

Индикатор для построения кривых уровня, заданный как разделенная разделенными запятой парами, состоящая из 'Contour' и 'off' или 'on'. Задайте 'on' для построения графиков кривых уровня для XYData данные. Задайте уровни с Levels Пара "имя-значение".

Пример: 'Contour','on'

Типы данных: char | string

`'Levels'` - Уровни для контурного графика
`10` (по умолчанию) | положительное целое число | вектор значений уровня

Уровни для контурного графика, заданные как разделенная разделенными запятой парами, состоящая из 'Levels' и положительное целое число или вектор значений уровня.

Положительное целое число - Plot Levels как одинаково разнесенные контуры.
Вектор - График контуров на значениях в Levels.

Чтобы получить контурный график, установите Contour Пара "имя-значение" с 'on'.

Пример: 'Levels',16

Типы данных: double

Выходные аргументы

`h` - Указатели на графические объекты
вектор

Указатели на графические объекты, возвращенные как вектор.

Подробнее о