Фиксированный угол между осями Z двух систем координат
Ограничения

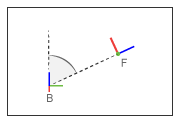
Этот блок применяет фиксированный угол между осями Z базовой и последующей систем координат портов. Системы координат теряют одну степень свободы вращения, если угол ограничения больше 0 ° и меньше 180 °. Они теряют две вращательные степени свободы, если угол ограничения в точности 0 ° или 180 ° - то есть, если системы координат параллельны или анти-параллельны. Рисунок показывает угол ограничения между двумя системами координат.
Тип ограничения угла. Настройкой по умолчанию является General.
| Напечатать | Цель |
|---|---|
Parallel | Выравнивание основы и последующей системы координат + оси Z. |
Anti-Parallel | Выровняйте базовую систему координат + ось Z с последующей рамкой -Z. |
Perpendicular | Сделайте основу и последующую системы координат Z осей перпендикулярными друг другу. |
General | Удерживайте заданный угол между осями Z системы координат базового и последующего портов. |
Угол ограничения между основой и последующей системой координат Z осей. Угол должен лежать в области значений 0 <, < 180 ° Для угла 0 или 180 град, установите Type равным Parallel или Anti-Parallel вместо этого. Значение по умолчанию 45 град.
Выберите, нужно ли вычислять и выводить вектор крутящего момента ограничения расстояния и его величину. Крутящий момент ограничения расстояния является крутящим моментом, который блок должен применить в порядок, чтобы сохранить угол, заданный вами между основой и последующими системами координат порта.
Ограничительные крутящие моменты действуют парами. Как выражено третьим законом движения Ньютона, если система координат базового порта оказывает ограничивающий крутящий момент на последующую систему координат порта, то система координат последующего порта должна оказывать равный и противоположный крутящий момент на систему координат базового порта. Выберите из двух ограничивающих моментов:
Follower on Base - Определите крутящий момент ограничения, который последующая система координат порта оказывает на базовую систему координат.
Base on Follower - Определите крутящий момент ограничения, который базовая система координат порта оказывает на последующую систему координат порта.
Блок выражает вектор крутящего момента ограничения с точки зрения его декартовых векторных компонентов. Разделение вектора на векторные компоненты известно как векторное разрешение. Система координат, оси которого определяют направления векторных компонентов, известна как система координат разрешения. Выберите, разрешать ли вектор крутящий момент ограничения в базовой или последующей системе координат порта.
Вычислите и выведите Декартовы компоненты вектора крутящего момента ограничения угла. Выходной сигнал является трехмерным вектором с компонентами, выраженными относительно осей X , Y и Z системы координат разрешения.
Вычислите и выведите величину крутящего момента ограничения угла, включая его знак.
Блок обеспечивает два порта системы координат:
B - порт базовой системы координат
F - Последующий порт системы координат
В сложение блок обеспечивает два порта выхода физического сигнала:
t - Вектор крутящего момента ограничения угла
tm - Сигнальная величина крутящего момента ограничения угла
Bevel Gear Constraint | Common Gear Constraint | Deep Learning Toolbox | Distance Constraint | Global Optimization Toolbox | Point on Curve Constraint | Rack and Pinion Constraint | Reinforcement Learning Toolbox | ga (Global Optimization Toolbox) | rlDDPGAgent(Набор Reinforcement Learning Toolbox)