В Simscape™ Multibody™ вы приводите в действие соединение непосредственно с помощью блока соединений. В зависимости от применения, входные параметры приведения в действие соединений могут включать в себя переменные сила/крутящий момент или движение. В этом примере вы предписываете крутящий момент приведения в действие для шарнирного соединения в модели четырехзвенника.
Блоки Transform Sensor добавляют измерение движения в модель. Можно построить график измеренных переменных и использовать графики для кинематического анализа. В этом примере вы строите графики кривых сцепки трех четырехзвенников: кривошипно-шатунного, двухколенчатого и двухскоростного.
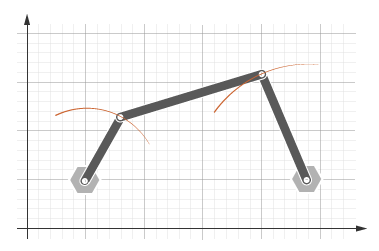
Четырехзвенник содержит четыре ссылки, которые соединяются с четырьмя шарнирами вращения, образуя плоский замкнутый цикл. Это редактирование преобразует движение входной ссылки в движение выходной ссылки. В зависимости от относительных длин четырёх ссылок четырехзвенника может преобразовать вращение во вращение, вращение в колебание или колебание в колебание.
Ссылки идут по разным именам согласно их функциям в четырехзвенник. Для примера сцепка ссылок передавать движение между кривошипными и шатунными ссылками. В таблице перечислены различные типы ссылок, которые можно найти в четырехзвеннике.
| Ссылка | Движение |
|---|---|
| Заводная рукоятка | Вращается относительно земли ссылки |
| Рокер | Колебания относительно земли ссылки |
| Сцепной прибор | Передает движение между кривошипными и шатунными ссылками |
| Земля | Твердое соединение четырехзвенника с миром или другой подсистемой |
Обычно ссылки имеют сложные формы. Это особенно относится к заземляющей ссылке, которая может быть просто фиксатором, удерживающим две поворотные опоры, которые соединяются с кривошипными или шатунными ссылками. Можно идентифицировать ссылки со сложными формами как жесткий участок между двумя смежными шарнирами вращения. В примере Модель Кинематической Цепи Замкнутой Системы, жесткий диапазон между двумя шарнирными установками представляет ссылку заземления.
Тип преобразования движения, которое обеспечивает четырехзвенник, зависит от типов ссылок, которые он содержит. Для примера четырехзвенник, который содержит две кривошипные ссылки, преобразует вращение на вход ссылки во вращение на выход ссылки. Этот тип редактирования известен как двойное кривошипное редактирование. Другие комбинации ссылок обеспечивают различные типы преобразования движения. Таблица описывает различные типы четырехзвенников, которые можно смоделировать.
| Редактирование | Движение ввода-вывода |
|---|---|
| Кривошип-качалка | Непрерывное вращение-колебание (и наоборот) |
| Двойной кривошип | Непрерывное вращение-непрерывное вращение |
| Двойной качалка | Колебания-колебания |
Теорема Грашофа предоставляет основное условие, которое четырехзвенник должна удовлетворить, чтобы по крайней мере одна ссылка завершила полный оборот. Согласно этой теореме, четырехзвенник содержит один или несколько кривошипных ссылки, если совокупная длина самых коротких и самых длинных ссылок не превышает совокупную длину двух остальных ссылок. Математически условие Грашофа является:
| s + l ≤ p + q | (1) |
s - самая короткая ссылка
l - самая длинная ссылка
p и q являются двумя оставшимися ссылками
Грашоф- редактирование может быть трех различных типов:
Кривошип-качалка
Двойной кривошип
Двойной качалка
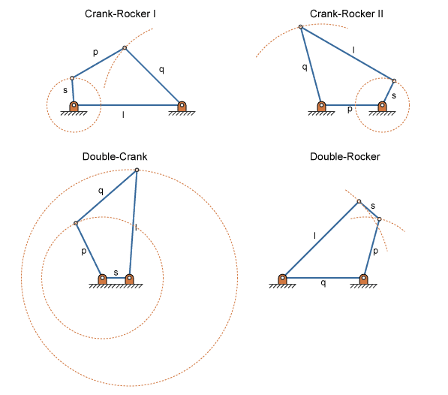
Изменив наземную ссылку, можно изменить тип редактирования Grashof. Для примера, путем присвоения кривошипной ссылки кривошипно-шатунного редактирования в качестве наземной ссылки, вы получаете двухколенчатое редактирование. Рисунок показывает четыре редактирований, которые вы получаете, меняя наземную ссылку.
В этом примере вы выполняете две задачи. Сначала вы добавляете вход приведения в действие крутящего момента в модель. Затем вы ощущаете движение кривошипных и шатунных ссылок относительно лабораторной системы координат. Вход приведения в действие является крутящим моментом, который вы прикладываете к соединению, соединяющему основу с кривошипной ссылкой. Поскольку вы прикладываете крутящий момент к шарниру, можно добавить этот крутящий момент непосредственно через блок соединений. Блок, к которому вы добавляете вход приведения в действие, называется Base-Crank Revolute Joint.
Вы добавляете вход приведения в действие к блоку соединений через входной порт физического сигнала. Этот порт по умолчанию скрыт. Чтобы отобразить его, вы должны выбрать Provided by Input из раскрывающегося списка Actuation > Torque.
Затем можно задать значение крутящего момента с помощью Simscape или Simulink® блоки. Если вы используете блоки Simulink, необходимо использовать блок Simulink-PS Converter. Этот блок преобразует сигнал Simulink в физический сигнал, который может использовать Simscape Multibody. Для получения дополнительной информации см. «Приведение в действие и измерение физическими сигналами».
Чтобы почувствовать движение кривошипного и шатунного звена, вы используете блок Transform Sensor. С помощью этого блока можно почувствовать движение между любыми двумя системами координат в модели. В этом примере вы используете его, чтобы определить координаты [ Y Z ] кривошипных и шатунных ссылок относительно лабораторной системы координат.
Выходные порты физического сигнала блоков Transform Sensor по умолчанию скрыты. Чтобы отобразить их, необходимо выбрать соответствующие выходы движения. Используя PS-Simulink Converter, можно преобразовать выходы физического сигнала в сигналы Simulink. Затем можно подключить получившиеся сигналы Simulink к другим блокам Simulink.
В этом примере вы выводите координаты кривошипного и шатунного звена в рабочую область с помощью блоков To Workspace Simulink. Выходы этих блоков обеспечивают базис для фазовых графиков, показывающих различные пути ссылки.
Предоставьте входной параметр, задайте внутреннюю механику соединения и определите координаты положения соединителя ссылки систем координат концов.
В MATLAB® в командной строке введите smdoc_four_bar. Откроется четырехзвенник модель. Для получения инструкций о том, как создать эту модель, смотрите Модель Кинематической Цепи Замкнутой Системы.
В диалоговом окне «База-Кривошипное соединение», в раскрывающемся списке Actuation > Torque, выберите Provided by Input. Блок предоставляет входной порт физического сигнала, маркированный t.
Перетащите эти блоки в модель. Блоки позволяют вам задать сигнал крутящего момента приведения в действие.
| Библиотека | Блок |
|---|---|
| Simulink> Sources | Constant |
| Simscape> Utilities | Simulink-PS Converter |
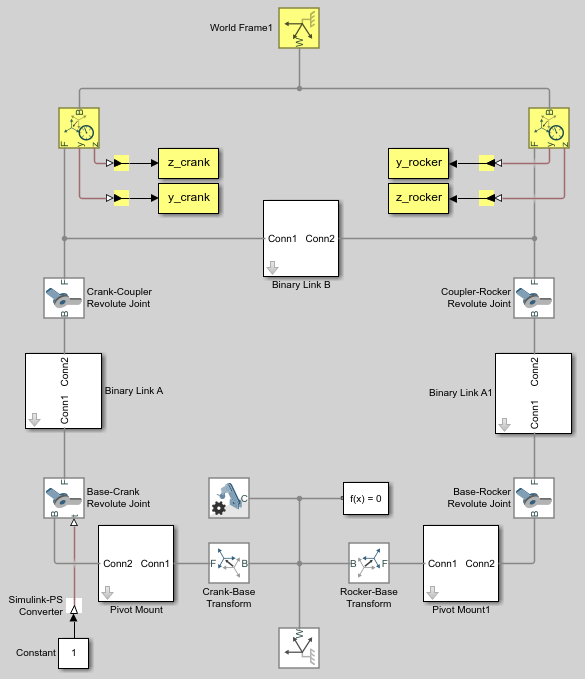
Соедините блоки как показано на рисунке. Новые блоки заштрихованы серым цветом.
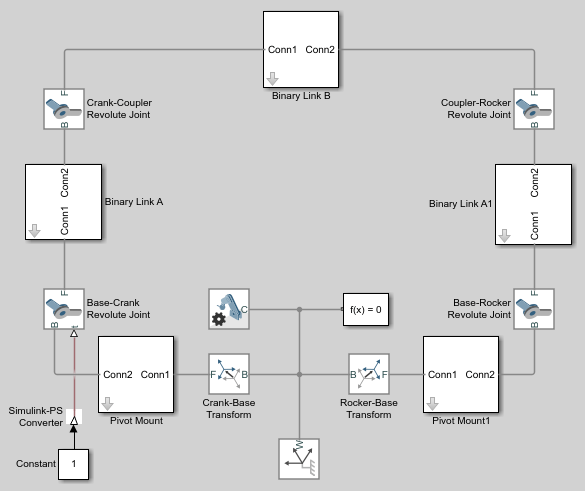
Действительные соединения рассеивают энергию из-за демпфирования. Демпфирование соединений можно задать непосредственно в диалоговых окнах блока. В каждом Диалоговом окне блока Revolute Joint в разделе Internal Mechanics > Damping Coefficient введите 5e-4 и нажмите OK.
Добавьте эти блоки к модели. Блоки позволяют вам чувствовать положение системы координат во время симуляции.
| Библиотека | Блок | Количество |
|---|---|---|
| Simscape> Multibody> Frames and Transforms | Transform Sensor | 2 |
| Simscape> Multibody> Frames and Transforms | World Frame | 1 |
| Simscape> Utilities | PS-Simulink Converter | 4 |
| Simulink> Sinks | To Workspace | 4 |
В Преобразование Sensor диалоговых окон блока выберите Translation > Y и Translation > Z. Измените размер блока по мере необходимости.
В Output signal unit параметрах диалоговых окон блока PS-Simulink Converter введите cm.
В Variable Name параметрах To Workspace диалоговых окон блока введите имена переменных:
y_crank
z_crank
y_rocker
z_rocker
Соедините и назовите блоки как показано на рисунке, повернув их по мере необходимости. Убедитесь, что блоки To Workspace с z_crank и z_rocker именами переменных соединяются с портами z системы координат блоков Transform Sensor. Новые блоки заштрихованы желтым цветом.
Запустите симуляцию. Это можно сделать на панели инструментов Simulink, нажав кнопку run. Mechanics Explorer воспроизводит основанную на физике анимацию сборки четырехзвенников.

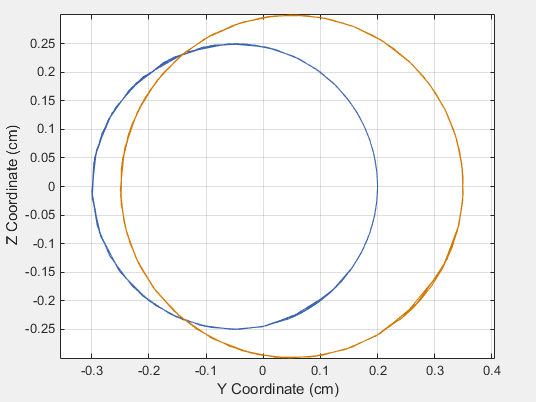
После окончания симуляции можно построить график координат положения систем координат концов соединительной ссылки, например, путем ввода следующего кода в командной строке MATLAB:
figure;
plot(y_crank.data, z_crank.data, 'color', [60 100 175]/255);
hold;
plot(y_rocker.data, z_rocker.data, 'color', [210 120 0]/255);
xlabel('Y Coordinate (cm)');
ylabel('Z Coordinate (cm)');
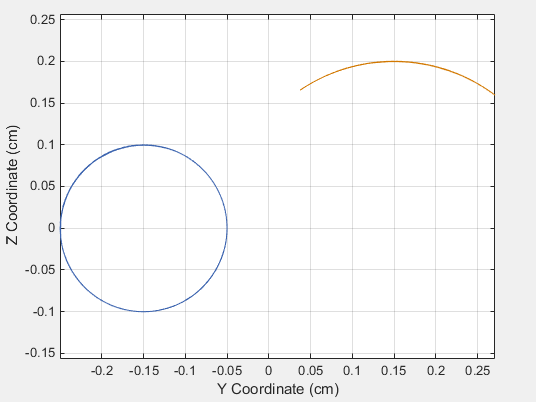
axis equal; grid on;Рисунок показывает график, который откроется. Этот график показывает, что кривошип завершает полный оборот, в то время как качалка завершает частичный оборот, например, он колеблется. Такое поведение характерно для кривошипно-шатунных систем.
Попробуйте симулировать модель в режиме двойного кривошипа. Можно изменить четырехзвенник на двухколенчатое редактирование путем изменения двоичных длин ссылки в соответствии с таблицей.
| Блок | Параметр | Значение |
|---|---|---|
| Двоичная ссылка A | Length | 25 |
| Двоичная ссылка B | Length | 20 |
| Двоичная ссылка A1 | Length | 30 |
| Преобразование кривошипа в основание | Translation> Offset | 5 |
| Преобразование базы Рокера | Translation> Offset | 5 |
Обновляйте и симулируйте модель. Рисунок показывает обновленное отображение визуализации в Mechanics Explorer.
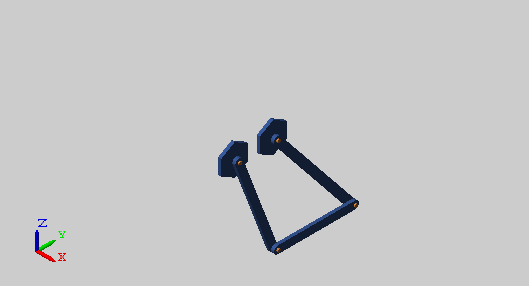
Постройте график координат положения систем координат концов ссылки. В командной строке MATLAB введите:
figure;
plot(y_crank.data, z_crank.data, 'color', [60 100 175]/255);
hold;
plot(y_rocker.data, z_rocker.data, 'color', [210 120 0]/255);
xlabel('Y Coordinate (cm)');
ylabel('Z Coordinate (cm)');
axis equal; grid on;Рисунок показывает график, который откроется. Этот график показывает, что обе ссылки завершают полный оборот. Такое поведение характерно для двойных редактирований.