Можно измерить поворот системы координат в разных форматах. Они включают угол-ось, кватернион и преобразование. Различные форматы доступны через блок Transform Sensor и, в ограниченной степени, в блоках соединений [1] . Выбор формата измерения зависит от модели. Выберите наиболее удобный для приложения формат.
Вращение является относительной величиной. Вращение одной системы координат имеет значение только относительно другой системы координат. Как таковые, блоки с возможностью измерения вращения требуют двух систем координат для измерения: измеренных и опорных систем координат. В этих блоках порт последующей системы координат идентифицирует измеренную систему координат; порт базовой системы координат идентифицирует опорную систему координат измерения.
Simscape™ Multibody™ определяет форматы вращения согласно стандартным соглашениям. В некоторых случаях существует несколько конвенций. Это относится, например, к кватерниону. Чтобы правильно интерпретировать измерения вращения, проверьте определения форматов вращения.
Ось-угол является одним из более простых форматов измерения поворота. Этот формат использует два параметра, чтобы полностью описать поворот: вектор оси и угол. Полезность формата ось-угол вытекает непосредственно из теоремы Эйлера о повороте. Согласно теореме, любая последовательность вращения или вращения 3-D может быть описана как чистое вращение вокруг одной фиксированной оси.
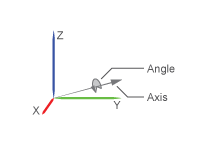
Чтобы измерить поворот системы координат в формате ось-угол, используйте блок Transform Sensor. Диалоговое окно блока содержит отдельные Axis и Angle параметры, которые можно выбрать, чтобы выставить соответствующие порты физического сигнала (PS) (маркированные оси и q, соответственно). Поскольку параметры угол-ось перечислены отдельно, можно выбрать для измерения ось, угол или оба.
Ось выхода является вектором 3D модуля в форме [ax, ay, az]. Этот единичный вектор кодирует направление поворота в соответствии с правилом правой руки. Например, система координат, вращающаяся в направлении против часовой стрелки вокруг оси + X, имеет ось вращения [1 0 0]. Система координат, вращающаяся по часовой стрелке вокруг той же оси, имеет ось вращения [-1 0 0].
Выход угла является скалярным числом в области значений 0- Это число кодирует степень поворота вокруг измеренной оси. По умолчанию угол измеряется в радианах. Можно изменить модули угла в блоке PS-Simulink Converter, используемом для взаимодействия с Simulink® блоки.
Кватернион является представлением вращения, основанным на числах гиперкомплекса. Кватернион состоит из скалярной части, S, и вектора, V, part. скалярная часть кодирует угол поворота, а векторная часть кодирует ось вращения.
Ключевым преимуществом кватернионов является пространство параметров без сингулярности. Математические особенности, которые присутствуют в угловых последовательностях Эйлера, приводят к потере вращательных степеней свободы. Это явление известно как карданный замок. В Simscape Multibody gimbal lock вызывает числовые ошибки, которые приводят к отказу симуляции. Отсутствие особенностей означает, что кватернионы более устойчивы для целей симуляции.
Чтобы измерить поворот системы координат в формате кватерниона, используйте:
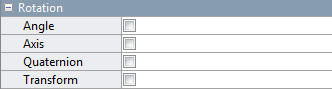
A Transform Sensor блок при измерении поворота между двумя общими системами координат. Меню Rotation диалогового окна содержит параметр Quaternion, который можно выбрать, чтобы открыть соответствующий порт физического сигнала (маркированный Q).

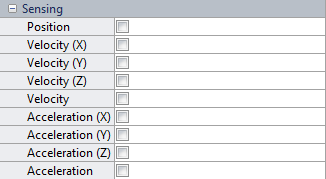
Блок соединений, который имеет сферический примитив при измерении 3-D вращения между двумя системами координат шарнира. Меню Sensing диалогового окна содержит параметр Position, который можно выбрать, чтобы открыть соответствующий порт физического сигнала (который также помечен Q). Для получения дополнительной информации см. Spherical Joint страницы с описанием блоков.
Кватернион на выходе является четырехэлементным вектором-строкой, , где:
и
θ - угол поворота, а [Ux, Uy, Uz] - единичный вектор оси вращения. Обратите внимание, что для любого заданного вращения существует два кватерниона. Они являются негативами друг друга, но представляют собой одно и то же вращение. Для примера кватернионы [1
0
0
0] и [-1
0
0
0] оба представляют ротацию тождеств.
Преобразование вращения является 3 × 3 матрицей, которая кодирует систему координат вращение. С точки зрения осей базовой системы координат [x, y, z] B, оси системы координат последователя [x, y, z] F:
Каждый матричный столбец содержит координаты последующей оси системы координат, разрешенной в базовой системе координат. Например, первый столбец содержит координаты последующей системы координат оси X, как разрешено в базовой системе координат. Точно так же второй и третий столбцы содержат координаты осей Y и Z, соответственно. Работа с вектором с матрицей вращения преобразует векторные координаты из последующей системы координат в базовую систему координат.
Можно почувствовать вращение системы координат в терминах матрицы вращения с помощью блока Transform Sensor. Диалоговое окно для этого блока содержит опцию Transform, которая, когда выбран, открывает порт физического сигнала с меткой R. Используйте этот порт для вывода сигнала матрицы вращения, например, для обработки и анализа в подсистеме Simulink - после преобразования выходного физического сигнала в сигнал Simulink через блок PS-Simulink Converter.

[1] Сварное соединение является исключением