Следующие примеры показывают, как расположить и сориентировать зубчатые тела так, чтобы они удовлетворяли требованиям сборки различных блоков ограничений зубчатых колес. Каждый пример начинается с обзора соответствующих размерностей передачи и расположения систем координат. Эти атрибуты управляют выбором твердых преобразований, необходимых для обеспечения того, чтобы передачи собирались в mesh.
Модели имеют одну и ту же топологию блоков, при этом компоненты модели - тела, соединения и ограничение передачи - в каждом случае расположены в кинематической замкнутой цепи. Рисунок показывает простой цикл. Несущее тело находится в примерах, которые считаются прикрепленными к лабораторной системе координат, инерция которого, следовательно, сводится к излишней детали, и тело полностью игнорируется.
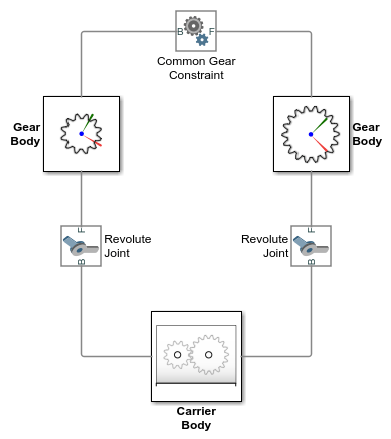
Модели содержат четыре типа блоков Simscape™ Multibody™:
File Solid - задает геометрию передачи, инерцию и цвета. Геометрия передачи, в комплекте с зубьями или резьбой, чтобы более четко показать передачи в mesh, импортируются из файлов STEP. Положения опорных систем координат зубчатых колес относительно геометрии зубчатых колес получаются из тех же файлов.
Соединение - Обеспечивает зубчатым телам необходимые степени свободы. Revolute Joint блоки позволяют вращать вокруг одной оси. Prismatic Joint блоки обеспечивают перемещение вдоль одной оси. Заданные в блоках соединений цели в состоянии скорости приводят передачи в движение.
Rigid Transform - Вращает и перемещает соединения и прикрепленные зубчатые тела так, чтобы они были правильно помещены для зацепления. Rigid Transform блоки обеспечивают средства для изменения расположения зубчатых колес и, следовательно, для удовлетворения требований к узлу зубчатых колес.
Ограничение передачи - соединяет движения зубчатых тел. Блоки ограничения передачи устраняют одну степень свободы между шестернями, заставляя их перемещаться как в mesh. Примеры показывают один за другим различные блоки ограничений передачи.

The smdoc_bevel_gear_start модель, показанная на рисунке, предоставляет пример узла конического зубчатого колеса. Модель, основанная на Bevel Gear Constraint блоке, завершена во всех смыслах, кроме единицы - все твердые преобразования равны нулю, и системы координат передач, следовательно, совпадают в пространстве.
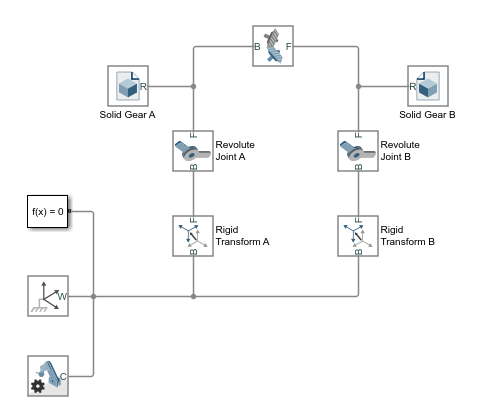
В этом кратком руководстве показано, как подходящие преобразования легко следуют из размерностей передачи и ограничений сборки - и как, после того как они заданы в Rigid Transform блоках, они позволяют модели передачи собираться как в mesh без ошибок.
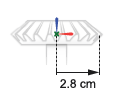
Конические передачи A и B идентичны по размеру с радиусом тангажа 2.8 cm в каждом случае. Опорные системы координат зубчатых колес расположены с источниками в центрах зубчатых колес и z осями, совмещенными с осями вращения зубчатых колес, так что они обращены в сторону от валов зубчатых колес. Это выравнивание согласуется с Revolute Joint блоками, которые допускают поворот только вокруг оси z.
Оси вращения шестерни встречаются под прямым углом. Система координат конического зубчатого колеса A находится со смещением [2.8, 0, 0] cm, в Декартовых координатах, относительно мировой системы координат. Система координат конической передачи B находится со смещением [0, 0, 2.8] cm относительно лабораторной системы координат и под углом 90 deg о y -оси также мировой системы координат.
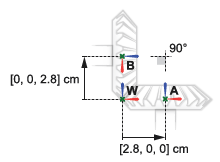
Завершите модель конического зубчатого колеса, задав твердые преобразования, описанные в схеме узла зубчатого колеса. Следующая концептуальная анимация показывает инкрементальные эффекты, которые твердые преобразования имели бы, если бы они применялись последовательно во время обновления модели.
Если вы еще не сделали этого, откройте неполную модель конической передачи, введя имя модели, smdoc_bevel_gear_start в MATLAB® командная строка.
В диалоговом окне Rigid Transform A блока задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение конического зубчатого колеса A относительно лабораторной системы координат, как описано в схеме Зубчатой Передачи.
| Параметр | Настройка |
|---|---|
| Method | Cartesian |
| Offset | [2.8, 0, 0] cm |
В диалоговом окне Rigid Transform B блока задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение конического зубчатого колеса B относительно лабораторной системы координат, как описано на схеме зубчатой передачи.
| Параметр | Настройка |
|---|---|
| Method | Cartesian |
| Offset | [0, 0, 2.8] cm |
В диалоговом окне Rigid Transform B блока задайте параметры Rotation, показанные в таблице. Эти параметры устанавливают ориентацию конической передачи B относительно лабораторной системы координат, как описано в схеме Зубчатой Передачи.
| Параметр | Настройка |
|---|---|
| Method | Standard Axis |
| Axis | +Y |
| Angle | 90 deg |
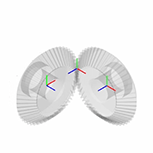
Симулируйте модель. В Mechanics Explorer откроется динамическая визуализация передачи, показанная в начале этого примера.
Чтобы увидеть полную модель конического зубчатого колеса, в командной строке MATLAB введите smdoc_bevel_gear. Simscape Multibody открывает модель конической передачи с твердыми преобразованиями, описанными в этом примере.

The smdoc_common_gear_external_start модель, показанная на рисунке, предоставляет пример внешнего узла цилиндрической передачи. Модель, основанная на Common Gear Constraint блоке, завершена во всех смыслах, кроме единицы - все твердые преобразования равны нулю, и системы координат передач, следовательно, совпадают в пространстве.
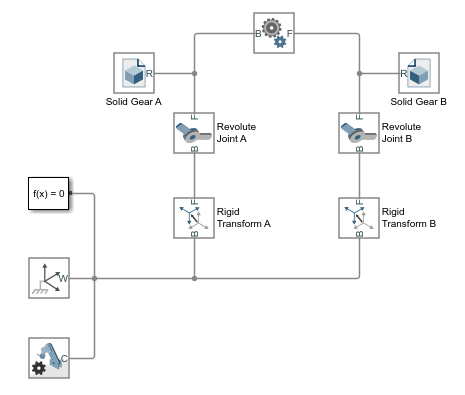
В этом кратком руководстве показано, как подходящие преобразования легко следуют из размерностей передачи и ограничений сборки - и как, после того как они заданы в Rigid Transform блоках, они позволяют модели передачи собираться как в mesh без ошибок.
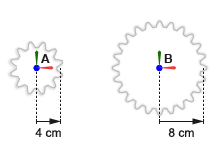
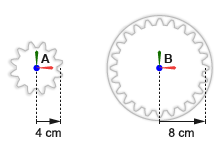
Малая цилиндрическая передача A имеет радиус тангажа 4 cm. Большая цилиндрическая шестерня B имеет радиус тангажа 8 cm. Опорные системы координат зубчатых колес расположены с источниками в центрах зубчатых колес и z осями, совмещенными с осями вращения зубчатых колес, так что они обращены в сторону от валов зубчатых колес. Это выравнивание согласуется с Revolute Joint блоком, который позволяет вращать только вокруг оси z.
Оси вращения цилиндрической шестерни параллельны друг другу. Система координат малой цилиндрической шестерни находится со смещением [-4, 0, 0] cm, в Декартовых координатах, относительно мировой системы координат. Система координат большой цилиндрической шестерни находится со смещением [-8, 0, 0] cm, также относительно мировой системы координат.
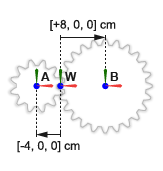
Завершите модель внешней цилиндрической шестерни, задав твердые преобразования, описанные в схеме узла зубчатой передачи. Следующая концептуальная анимация показывает инкрементальные эффекты, которые твердые преобразования имели бы, если бы они применялись последовательно во время обновления модели.
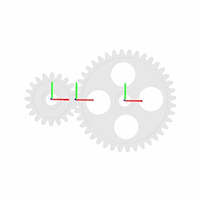
Если вы еще не сделали этого, откройте неполную модель конической передачи, введя имя модели, smdoc_common_gear_external_start в командной строке MATLAB.
В диалоговом окне Rigid Transform A блока задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение малой цилиндрической шестерни A относительно лабораторной системы координат, как описано в схеме Зубчатой Передачи.
| Параметр | Настройка |
|---|---|
| Method | Cartesian |
| Offset | [-4, 0, 0] cm |
В диалоговом окне Rigid Transform B блока задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение большой цилиндрической шестерни B относительно лабораторной системы координат, как описано в схеме Зубчатой Передачи.
| Параметр | Настройка |
|---|---|
| Method | Cartesian |
| Offset | [8, 0, 0] cm |
Симулируйте модель. В Mechanics Explorer откроется динамическая визуализация передачи, показанная в начале этого примера.
Чтобы увидеть полную модель внешнего привода, в командной строке MATLAB введите smdoc_common_gear_external.

The smdoc_common_gear_internal_start модель, показанная на рисунке, предоставляет пример внутреннего узла цилиндрической шестерни. Модель, основанная на Common Gear Constraint блоке, завершена во всех смыслах, кроме единицы - все твердые преобразования равны нулю, и системы координат передач, следовательно, совпадают в пространстве.

В этом кратком руководстве показано, как подходящие преобразования легко следуют из размерностей передачи и ограничений сборки - и как, после того как они заданы в Rigid Transform блоках, они позволяют модели передачи собираться как в mesh без ошибок.
Прямозубая шестерня A имеет радиус тангажа 4 cm. Кольцевая шестерня B имеет радиус тангажа 8 cm. Опорные системы координат зубчатых колес расположены с источниками в центрах зубчатых колес и z осями, совмещенными с осями вращения зубчатых колес, так что они обращены в сторону от валов зубчатых колес. Это выравнивание согласуется с Revolute Joint блоком, который позволяет вращать только вокруг оси z.
Оси вращения шестерни параллельны друг другу. Система координат цилиндрической шестерни находится со смещением [-4, 0, 0] cm, в декартовом обозначении, относительно мировой системы координат. Система координат кольцевой передачи находится слева с источником и z осью, совпадающей с осями лабораторной системы координат .
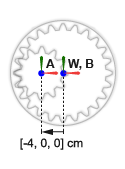
Завершите модель внутренней цилиндрической шестерни, задав твердые преобразования, описанные в схеме узла зубчатой передачи. Следующая концептуальная анимация показывает инкрементальные эффекты, которые твердые преобразования имели бы, если бы они применялись последовательно во время обновления модели.
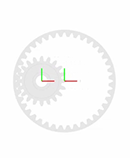
Если вы еще не сделали этого, откройте неполную модель конической передачи, введя имя модели, smdoc_common_gear_internal_start в командной строке MATLAB.
В диалоговом окне Rigid Transform A блока задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение цилиндрической передачи A относительно лабораторной системы координат, как описано в схеме Зубчатой Передачи.
| Параметр | Настройка |
|---|---|
| Method | Cartesian |
| Offset | [-4, 0, 0] cm |
Симулируйте модель. В Mechanics Explorer откроется динамическая визуализация передачи, показанная в начале этого примера.
Чтобы увидеть полную модель внутренней цилиндрической передачи, в командной строке MATLAB введите smdoc_common_gear_internal.
The smdoc_rack_and_pinion_start модель, показанная на рисунке, предоставляет пример блока «реечного механизма». Модель, основанная на Rack and Pinion Constraint блоке, завершена во всех смыслах, кроме единицы - все твердые преобразования равны нулю, и системы координат передач, следовательно, совпадают в пространстве.
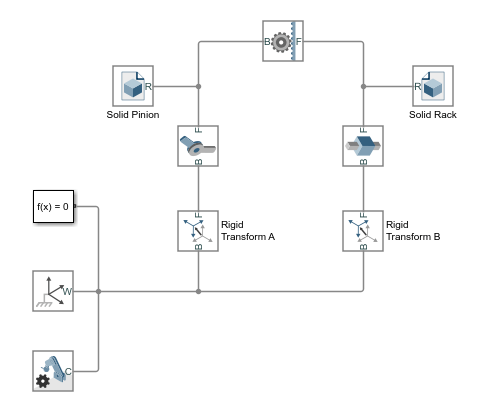
В этом кратком руководстве показано, как подходящие преобразования легко следуют из размерностей передачи и ограничений сборки - и как, после того как они заданы в Rigid Transform блоках, они позволяют модели передачи собираться как в mesh без ошибок.
Шестерня, A, имеет радиус тангажа 2 cm. Система координат шестерни расположена с источником в центре шестерни, а z ось - вдоль оси шестерни. Система координат стойки расположена с источником 3.75 cm от ребра стойки и z оси вдоль длины стойки. Выравнивания системы координат соответствуют Revolute Joint и Prismatic Joint блокам, которые допускают движение только вокруг оси z или вдоль нее.
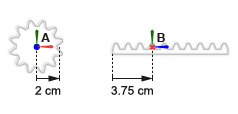
Ось перемещения стойки находится под прямым углом к оси вращения шестерни. Система координат шестерни находится со смещением [0, 2, 0] cm, в декартовом обозначении, относительно мировой системы координат. Система координат стойки находится под углом 90 deg относительно положительной y -оси лабораторной системы координат.

Завершите модель реечного механизма, задав твердые преобразования, описанные в схеме узла зубчатой передачи. Следующая концептуальная анимация показывает инкрементальные эффекты, которые твердые преобразования имели бы, если бы они применялись последовательно во время обновления модели.
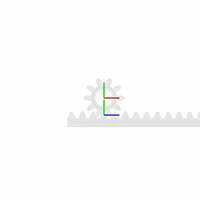
Если вы еще не сделали этого, откройте неполную модель конической передачи, введя имя модели, smdoc_rack_and_pinion_start в командной строке MATLAB.
В диалоговом окне Rigid Transform A блока задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение шестерни A относительно лабораторной системы координат, как описано в схеме Зубчатой Передачи.
| Параметр | Настройка |
|---|---|
| Method | Cartesian |
| Offset | [0, 2, 0] cm |
В диалоговом окне Rigid Transform B блока задайте параметры Rotation, показанные в таблице. Эти параметры определяют ориентацию стойки B относительно лабораторной системы координат, как описано в схеме Зубчатой Передачи.
| Параметр | Настройка |
|---|---|
| Method | Standard Axis |
| Axis | +Y |
| Angle | 90 deg |
Симулируйте модель. В Mechanics Explorer откроется динамическая визуализация передачи, показанная в начале этого примера.
Чтобы увидеть полную модель реечного механизма, в командной строке MATLAB введите smdoc_rack_and_pinion.
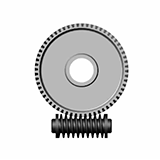
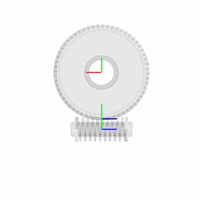
The smdoc_worm_and_gear_start модель, показанная на рисунке, предоставляет пример червячно-зубчатого узла. Модель, основанная на Worm and Gear Constraint блоке, завершена во всех смыслах, кроме единицы - все твердые преобразования равны нулю, и системы координат передач, следовательно, совпадают в пространстве.
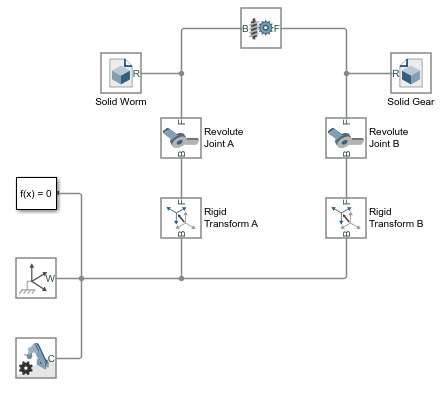
В этом кратком руководстве показано, как подходящие преобразования легко следуют из размерностей передачи и ограничений сборки - и как, после того как они заданы в Rigid Transform блоках, они позволяют модели передачи собираться как в mesh без ошибок.
Червь, A, имеет радиус тангажа 0.85 cm. Шестерня B имеет радиус тангажа 3.75 cm. Червячная и зубчатая опорные системы координат расположены с источниками в центрах геометрии и z осями, выровненными по соответствующим осям вращения. Это выравнивание согласуется с Revolute Joint блоком, который позволяет вращать только вокруг оси z.
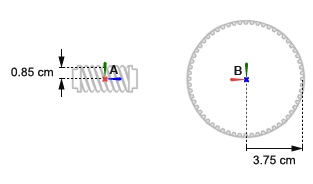
Ось вращения червяка находится под прямым углом к оси вращения зубчатой передачи. Червячная система координат находится со смещением [0, -0.85, 0] cm, в декартовом обозначении, относительно мировой системы координат. Система координат шестерни находится со смещением [0, +3.75, 0] cm и под углом 90 deg о положительной y -оси относительно лабораторной системы координат.
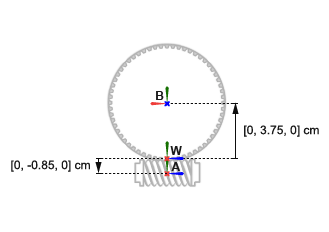
Завершите модель червячного привода, задав твердые преобразования, описанные в схеме зубчатого привода. Следующая концептуальная анимация показывает инкрементальные эффекты, которые твердые преобразования имели бы, если бы они применялись последовательно во время обновления модели.
Если вы еще не сделали этого, откройте неполную модель конической передачи, введя имя модели, smdoc_worm_and_gear_start в командной строке MATLAB.
В диалоговом окне Rigid Transform A блока задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение червячного элемента A относительно лабораторной системы координат, как описано в схеме Зубчатой Передачи.
| Параметр | Настройка |
|---|---|
| Method | Cartesian |
| Offset | [0, -0.85, 0] cm |
В диалоговом окне Rigid Transform A блока задайте параметры Translation, показанные в таблице. Эти параметры устанавливают положение передачи B относительно лабораторной системы координат, как описано в схеме Зубчатой Передачи.
| Параметр | Настройка |
|---|---|
| Method | Cartesian |
| Offset | [0, 3.75, 0] cm |
В диалоговом окне Rigid Transform B блока задайте параметры Rotation, показанные в таблице. Эти параметры устанавливают ориентацию передачи B относительно лабораторной системы координат, как описано в схеме Зубчатой Передачи.
| Параметр | Настройка |
|---|---|
| Method | Standard Axis |
| Axis | +Y |
| Angle | 90 deg |
Симулируйте модель. В Mechanics Explorer откроется динамическая визуализация передачи, показанная в начале этого примера.
Чтобы увидеть полную модель червячной передачи, в командной строке MATLAB введите smdoc_worm_and_gear.