Преобразуйте изменение усиления и фазы в изменение усиления на основе диска
В анализе полей диска изменения усиления и фазы моделируются как коэффициент F (s) умножающий L отклика разомкнутого контура (s). Этот фактор принимает значения в диске D с центром на действительной оси с реальными точками пересечения оси gmin и gmax. Запас диска определяет наибольший размер диска [gmin,gmax] для которого цикл обратной связи остается стабильным. Это обеспечивает запас по амплитуде не менее DGM = [gmin,gmax] а также некоторый запас по фазе DPM определяется геометрией диска.
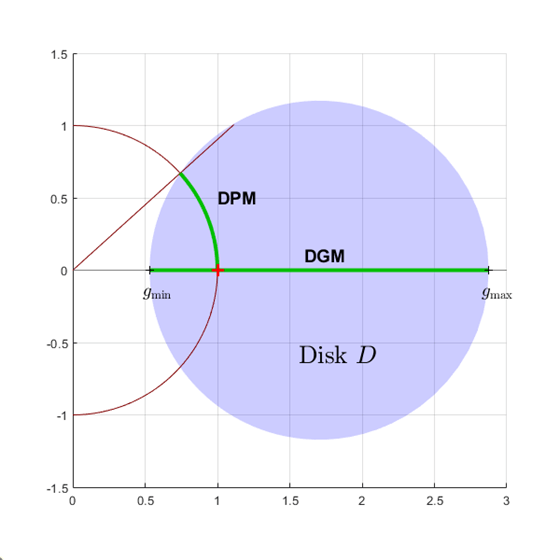
И наоборот, getDGM принимает желаемые запасы по усилению и фазе GM и PM и вычисляет наименьший дисковый D, который обеспечивает и то, и другое. Этот диск характеризуется реальными точками пересечения gmin, gmax и соответствующий дисковый запас по амплитуде DGM = [gmin,gmax] и коэффициент запаса по фазе DPM встретить или превысить GM и PM.
Для получения дополнительной информации о дисковой модели усиления и изменения фазы, см. Алгоритмы.
DGM = getDGM(GM,PM,'tight')GM и PM.
Если GM и PM являются скалярами, тогда диск захватывает коэффициент усиления, который может увеличиваться или уменьшаться в множителе GM, и фазу, которая может увеличиваться или уменьшаться на PM.
Если GM и PM являются векторами вида [glo,ghi] и [pmin,pmax] затем диск захватывает относительные изменения коэффициента усиления и фазы в этих областях значений.
Если либо GM или PM является [], что удаляет соответствующее ограничение на размер диска.
Выходы имеют вид DGM = [gmin,gmax], и описывает диск, который представляет абсолютные изменения усиления в этой области значений. Для образца, DGM = [0.8,1.8] модели усиление, которое может варьироваться от 0,8 номинального значения до 1,8 номинального значения, и изменения фазы, определяемые геометрией диска. Возможно, этот диск имеет ненулевую наклонность (см. Алгоритмы). Использование DGM для создания umargin блок, который моделирует эти изменения усиления и фазы.
Нахождение наименьшего дискового запаса усиления, который представляет относительное изменение усиления ± 6 дБ относительно номинального значения и изменения фазы ± 40 °. Преобразуйте изменение усиления в абсолютные модули.
GM = db2mag(6)
GM = 1.9953
PM = 40;
DGM = getDGM(GM,PM,'tight')DGM = 1×2
0.4299 1.9953
DGM описывает диск, который моделирует как изменения усиления, так и фазы. Значения в DGM представление области значений изменения усиления при отсутствии изменения фазы. Обратите внимание, что DGM область значений немного больше заданного [1/GM,GM] область значений, поскольку требование запаса по фазе является более строгим и определяет размер диска. Визуализируйте полную область значений изменений усиления и фазы, представленных DGM.
diskmarginplot(DGM)
'tight'constraint вычисляет наименьший диск, который обеспечивает как целевые изменения усиления, так и фазы, который не обязательно представляет симметричную область значений усиления. В этом случае диск представляет усиление, которое может уменьшиться несколько больше, чем может увеличиться. Исследуйте диск неопределенности, заданный этим конкретным DGM.
diskmarginplot(DGM,'disk')
Чтобы применить симметричные изменения усиления, используйте 'balanced' опция.
Определите дисковый запас по амплитуде, который обеспечивает симметричное изменение усиления 5 дБ и изменение фазы 30 степени.
GM = db2mag(5);
PM = 30;
DGM = getDGM(GM,PM,'balanced')DGM = 1×2
0.5623 1.7783
'balanced'constraint моделирует диск неопределенности, который симметричен вокруг номинального значения. Функция возвращает симметричный дисковый запас по амплитуде DGM = [gmin,gmax], с gmin=1/gmax.
diskmarginplot(DGM)
В этом случае DPM немного превышает целевое изменение фазы и DGM равен целевому изменению усиления.
Определите дисковый запас по амплитуде, соответствующий изменениям усиления между 90% и 160% от номинального значения и изменениям фазы от -15 до + 15 степени.
gainRange = [0.9,1.6];
phaseRange = [-15,15];
DGMt = getDGM(gainRange,phaseRange,'tight')DGMt = 1×2
0.8603 1.6000
'tight'constraint моделирует наименьший диск, который обеспечивает целевые изменения усиления и фазы. Этот диск моделируется с изменением усиления, которое наклоняется к увеличению усиления.
Также можно использовать 'balanced'опция, чтобы ограничить дисковый запас по амплитуде симметричной областью значений формы gmin = 1/gmax. Это означает, что коэффициент усиления может увеличиться или уменьшиться на равную величину.
DGMb = getDGM(gainRange,phaseRange,'balanced')DGMb = 1×2
0.6250 1.6000
Визуализируйте область значений одновременных изменений усиления и фазы, соответствующих обеим областям значений усиления.
diskmarginplot([DGMt;DGMb])
![Figure contains an axes. The axes with title Range of gain and phase variations contains 2 objects of type patch. These objects represent DGM = [0.86,1.6], DPM = 15, DGM = [0.625,1.6], DPM = 26.](../../examples/robust/win64/ComputeDiskMarginFromRangeOfGainAndPhaseVariationsExample_01.png)
Сбалансированная область значений DGMb моделирует больший, симметричный область значений усиления (gmin = 1/gmax) и большие изменения фазы, чем заданные вами. Если вы уверены, что коэффициент усиления изменяется больше в одном направлении, чем другой в вашей системе, то эта сбалансированная модель может быть чрезмерно консервативной.
Определите сбалансированные дисковые области значений запаса по запасу по амплитуде, которые обеспечивают изменения усиления ± 4 дБ, ± 6 дБ и ± 12 дБ и изменение фазы ± 30 °. Вы можете получить все дисковые области значений усиления сразу путем сложения необходимых целевых областей значений в вектор-столбец.
GM = db2mag([4;6;12]);
PM = 30;
DGM = getDGM(GM,PM,'balanced')DGM = 3×2
0.5774 1.7321
0.5012 1.9953
0.2512 3.9811
diskmarginplot(DGM)
![Figure contains an axes. The axes with title Range of gain and phase variations contains 3 objects of type patch. These objects represent DGM = [0.577,1.73], DPM = 30, DGM = [0.501,2], DPM = 36.8, DGM = [0.251,3.98], DPM = 61.8.](../../examples/robust/win64/DGMForMultipleTargetGainAndPhaseVariationsExample_01.png)
Каждая строка в матрице DGM задает дисковое изменение усиления для соответствующей записи в GM. Например, наименьший сбалансированный (симметричный) диск, который захватывает изменение усиления ± 4 дБ и изменение фазы ± 30 °, задан DGM(1,:) = [0.58 1.73].
Этот диск представляет несколько больше, чем целевой диск ± 4 дБ, чтобы захватить полное изменение коэффициента усиления ± 30 °. Для целей ± 6 дБ и ± 12 дБ диск точно соответствует целевому изменению усиления, но соответствующие диски описывают большие изменения фазы.
DGM - Смоделированная область значений относительных изменений усиленияСмоделированная область значений относительных изменений усиления, возвращенный как двухэлементный вектор вида [gmin,gmax], где gmin < 1 и gmax > 1. Для образца, DGM = [0.8 1.5] представляет усиление, которое может варьироваться между 80% и 150% от его номинального значения (то есть изменяться в множителе между 0,8 и 1,5). gmin может быть отрицательным, определяющим область значений относительных изменений усиления, который включает изменение знака. Когда вы используете 'balanced' опция, изменение усиления симметрично, то есть усиление может увеличиться или уменьшиться на ту же величину (gmin = 1/gmax).
Область области значений [gmin,gmax] описывает диск неопределенности усиления и фазы, где коэффициент усиления может варьироваться в зависимости от [gmin,gmax] и фаза может изменяться на величину, определяемую геометрией диска. Например, на следующем графике показан диск, характеризующийся DGM = [0.5,2] (Для получения дополнительной информации о дисковой модели неопределенности см. Алгоритмы). Соответствующее изменение фазы (возвращается в DPM) составляет ± 30 °.
![Uncertainty disk characterized by DGM = [0.5,2]](disk_dgm_argdesc.png)
В целом, DGM или соответствующее DPM может захватывать большие области значений изменений, чем те, которые вы задаете с входы GM и PM. Диск всегда захватывает по крайней мере указанные изменения.
Если GM является вектору-столбцу или матрицам, представляющим несколько целевых области значений изменения усиления, DGM - двухколоночная матрица вида [gmin1,gmax1; ...;gminN,gmaxN], где каждая строка является соответствующей дисковой областью значений усиления.
DPM - Изменение фазы на основе дискаДисковый запас по фазе, возвращенный как двухэлементный вектор вида [-pm,pm]. Величина изменения фазы определяется геометрией диска, описанной DGM (см. Алгоритмы).
Если PM - вектор-столбец или матрицы, представляющие несколько целевых области значений изменения фазы, DPM - двухколоночная матрица вида [-pm1,pm1; ...;-pmN,pmN], где каждая строка является соответствующей дисковой областью значений усиления.
umargin и diskmargin моделируют изменения усиления и фазы в индивидуальном канале обратной связи как частотно-зависимый мультипликативный коэффициент F (s), умножающий номинальную L отклика без разомкнутого контура (s), так что возмущенная характеристика является L (s) F (s). Коэффициент F (s) параметризован:
В этой модели,
δ (s) является динамической неопределенностью с ограничением по усилению, нормированной так, что она всегда изменяется внутри единичного диска (||<reservedrangesplaceholder0>||∞ < 1).
ɑ устанавливает величину усиления и изменения фазы, смоделированные F. Для фиксированных σ параметр ɑ управляет размером диска. Для ɑ = 0 мультипликативный коэффициент равен 1, соответствующий номинальной L.
σ, называемое skew, смещает смоделированную неопределенность в сторону увеличения или уменьшения усиления.
Коэффициент F принимает значения в диске с центром на действительной оси и содержащем номинальное значение F = 1. Диск характеризуется своей точкой пересечения DGM = [gmin,gmax] с действительной осью. gmin < 1 и gmin > 1 - минимальные и максимальные относительные изменения в усилении, моделируемые F, в номинальной фазе. Фаза неопределенность, смоделированная F, является областью значений DPM = [-pm,pm] значений фазы при номинальном усилении (|<reservedrangesplaceholder1>| = 1). Например, на следующем графике правая сторона показывает дисковое F, которое пересекает действительную ось в интервале [0.71.1.4]. Левая сторона показывает, что этот диск моделирует изменение усиления ± 3 дБ и изменение фазы ± 19 °.
DGM = [0.71,1.4]
F = umargin('F',DGM)
plot(F)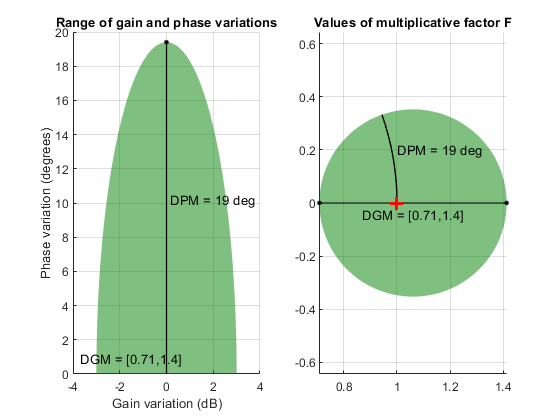
getDGM преобразует целевые изменения усиления и фазы, которые вы хотите смоделировать, в дисковую область значений изменения усиления DGM. Эта область значений полностью характеризует дисковые F. Соответствующая область значений фаз DPM определяется таким образом DGM и модель диска.
Для получения дополнительной информации о модели неопределенности для изменений усиления и фазы, смотрите анализ устойчивости с использованием полей диска.