Визуализация дисковых запасов устойчивости
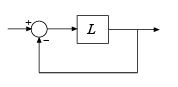
diskmarginplot( строит графики дискового коэффициента усиления и запасов по фазе для цикла отрицательной обратной связи SISO или MIMO L)feedback(L,eye(N)), где N количество входов и выходов в разомкнутый контур отклике L.
Для ответов MIMO, diskmarginplot строит графики мультициклов многолучевого диска. Дисковый запас по амплитуде на каждой частоте ± GM, где GM - значение, показанное на графике в дБ. Аналогично, дисковый запас фазы составляет ± PM степеней, где PM - значение, показанное на графике. Для получения дополнительной информации о дисковых полях усиления и фазы смотрите diskmargin.
diskmarginplot(___, строит графики дискового коэффициента усиления и запасов по фазе, вычисленных с помощью косой sigma)sigma смещение изменения усиления в сторону увеличения усиления (sigma > 0) или уменьшение усиления (sigma < 0). Если вы использовали diskmargin для получения дисковых полей с некоторыми конкретными sigma, можно использовать этот синтаксис, чтобы увидеть частотную зависимость полей при этом sigma значение. Для sigma ≠ 0 нанесенное на график значение GM = min(gmax,1/max(0,gmin)). Другими словами, график показывает наибольшую величину изменения усиления [1/GM,GM] который помещается в пределах дискового запаса по амплитуде [gmin,gmax] системы на заданном sigma.
diskmarginplot(___, строит графики полей на частотах, заданных w)w.
Если w - массив ячеек вида {wmin,wmax}, затем на графике показаны поля на частотах, расположенных между wmin и wmax.
Если w является вектором частот, тогда график показывает поля на каждой заданной частоте.
diskmarginplot( строит график области значений одновременных изменений усиления и фазы, соответствующих дисковому запасу по амплитуде. График также показывает максимальные изменения только коэффициент усиления и только фазы (эти дисковые коэффициенты усиления и запасов по фазе). DGM)DGM является вектором вида [gmin,gmax]. Область запаса по амплитуде DGM может также быть скаляром, что эквивалентно заданию симметричного изменения усиления [1/DGM,DGM]. Чтобы построить области значений для нескольких дисковых запасов по амплитуде сразу, используйте двухколоночную матрицу формы [gmin1,gmax1;...;gminN,gmaxN]. Для получения дополнительной информации о дисковых запасах по амплитуде см. diskmargin.
diskmarginplot( строит графики на комплексном диске смоделированных изменений усиления и фазы, соответствующих дисковому запасу по амплитуде DGM,'disk')DGM. Для получения дополнительной информации о том, как анализ полей на диске моделей коэффициент усиления и изменений фазы, смотрите анализ устойчивости с использованием полей на диске.
diskmarginplot( строит график области исключения в плоскости Найквиста, соответствующей полю диска DGM,'nyquist')DGM. Требование, чтобы система с обратной связью оставалась стабильной для изменения усиления или фазы в диске, соответствующем DGM равносильно требованию, чтобы реакция без разомкнутого контура оставалась вне дискообразной области исключения в плоскости Найквиста. Дополнительные сведения см. в разделе Анализ устойчивости с использованием полей на диске.
diskmarginplot( строит график области значений изменений усиления и фазы, соответствующих размеру диска alpha,sigma,___)alpha и перекос sigma. Если либо alpha или sigma является вектором, тогда график включает области значений для всех заданных значений. Если оба alpha и sigma являются векторами, тогда график включает области значений для пар alpha1,sigma1;...;alphaN,sigmaN.
Чтобы построить график смоделированного диска неопределенности, соответствующего alpha, sigma, используйте этот синтаксис с 'disk' флаг. Чтобы построить график соответствующего диска исключения в плоскости Nyquist, используйте этот синтаксис со 'nyquist' флаг.
diskmarginplot( рисует график на осях, заданных указателем на ось (AX,___)axes или UIaxes объект). Используйте этот аргумент для задания осей при создании приложений в Develope Apps Using App Designer. Можно использовать этот аргумент с любым из предыдущих синтаксисов, чтобы нарисовать любой из графиков, которые diskmarginplot может сгенерировать.
Постройте график дискового усиления и запасов по фазе системы с разомкнутым контуром откликом L и ответ с обратной связью feedback(L,1).
L = tf(25,[1 10 10 10]); diskmarginplot(L)
Дисковый запас по амплитуде на каждой частоте, по меньшей мере ±GM, где GM - значение, показанное на графике в дБ. Точно так же дисковый запас по фазе ±PM степени. Дисковые поля, возвращенные diskmargin команда является наименьшими полями по частоте. (Щелкните правой кнопкой мыши график и выберите «Характеристики» > «Минимальное поле диска» для всплывающей подсказки, содержащей информацию об этих минимальных полях.)
Сравните дисковое усиление и запасы по фазе двух разомкнутых контуров характеристик на одном графике.
L1 = tf(25,[1 10 10 10]); L2 = tf([1 100],[1 10 20 50]); diskmarginplot(L1,L2)
Настроить внешний вид графиков можно с помощью LineSpec аргумент. Снова постройте графики полей, используя синюю штриховую линию для L1 и красные точки для L2.
diskmarginplot(L1,'b--',L2,'r.')
Дисковые запасы по амплитуде возвращаются diskmargin предположим, что нет изменения фазы, и запасы по фазе не предполагают изменения усиления. На практике системы испытывают как изменение усиления, так и изменение фазы одновременно. Анализ дисковой маржи учитывает такие одновременные изменения коэффициента усиления и фазы.
Вычислите дисковое усиление и запасы по фазе системы. Затем используйте diskmarginplot визуализация соответствующих допустимых областей значений одновременного усиления и изменения фазы.
L = tf(25,[1 10 10 10]); DM = diskmargin(L); DGM = DM.GainMargin
DGM = 1×2
0.6273 1.5942
DPM = DM.PhaseMargin
DPM = 1×2
-25.8017 25.8017
diskmarginplot(DGM)
Затененная область на графике показывает область значений одновременных изменений усиления и фазы, которые сохраняют стабильность системы с обратной связью feedback(L,1). Когда нет изменения фазы, система может терпеть полную область значений изменения усиления DGM, от -4 дБ до 4 дБ. Если фазе позволено изменяться примерно на ± 20 степени, допустимая область значений изменения усиления падает примерно до -2,5 дБ до 2 дБ. При полной области значений изменений фазы ± 26 степени система не может терпеть изменения усиления.
Чтобы визуализировать несколько области значений на одном графике, объедините их в двухколоночный вектор. Например, вычислите поля диска L с положительным и отрицательным перекосом и постройте график всей трёх областей значений изменений вместе.
DMn = diskmargin(L,-2); DGMn = DMn.GainMargin; DMp = diskmargin(L,2); DGMp = DMp.GainMargin; DGMall = [DGMn;DGM;DGMp]; diskmarginplot(DGMall)
![Figure contains an axes. The axes with title Range of gain and phase variations contains 3 objects of type patch. These objects represent DGM = [0.401,1.37], DPM = 29.1, DGM = [0.627,1.59], DPM = 25.8, DGM = [0.772,1.72], DPM = 21.](../../examples/robust/win64/CombinedGainAndPhaseVariationExample_02.png)
Этот график показывает, что цикл обратной связи может переносить большие изменения усиления и фазы, когда коэффициент усиления уменьшается. Другими словами, стабильность цикла более чувствительна к увеличению усиления. Для получения дополнительной информации о том, как изменение перекоса влияет на дисковые оценки запаса по амплитуде и фазе, смотрите Анализ устойчивости с использованием полей диска.
Дисковый анализ запаса по амплитуде моделирует коэффициент усиления и изменение фазы как неопределенный коэффициент F, умножая коэффициент усиления без разомкнутого контура L. (Для получения дополнительной информации об этой модели см. Анализ устойчивости с использованием полей диска.) Стабильная область значений изменений усиления и фазы, возвращаемых diskmargin команда эквивалентна диску с значениями F, для которого замкнутый цикл является стабильным. Когда вы получаете дисковое усиление и запасы по фазе системы, можно использовать diskmarginplot для визуализации соответствующего диска значений F.
L = tf(25,[1 10 10 10]); DM = diskmargin(L); DGM = DM.GainMargin
DGM = 1×2
0.6273 1.5942
diskmarginplot(DGM,'disk')
График показывает значения F в комплексной плоскости, где ось X является вещественной частью, а ось Y - мнимой детальи. дисковый запас по амплитуде DGM однозначно определяет этот диск и соответствующий дисковый запас по фазе, DPM.
Диск F неопределенности параметризуется двумя значениями: α, который устанавливает размер диска и σ, который оказывает влияние на изменение выгоды к увеличению выгоды или уменьшению. Эта параметризация задается:
,
где и - нормированная неопределенность. (Для получения дополнительной информации смотрите Анализ устойчивости с использованием полей диска.) Для заданной области значений изменений усиления можно использовать gm2dm для преобразования дискового запаса по амплитуде DGM к значениям α и, которые описывают соответствующий диск. diskmarginplot может построить график F-диска для заданной пары α ,
DGM = [0.8,2]
DGM = 1×2
0.8000 2.0000
[alpha,sigma] = gm2dm(DGM);
diskmarginplot(alpha,sigma,'disk')
В этом случае σ больше, чем нуль потому что дисковая область значений выгоды DGM = [0,8,2] включает увеличение усиления больше, чем уменьшение. .r= 0 представляет коэффициент усиления, который может увеличиться настолько, насколько может уменьшиться. , < 0 представляет область значений с большим уменьшением, чем увеличение. Подготовьте диск F для различных значений σ, чтобы видеть, как область значений выгоды (диаметр диска) меняется в зависимости от σ.
sigma = [-3,0,3];
diskmarginplot(alpha,sigma,'disk')
Для фиксированного и α управляет размером диска, а значит, и количеством смоделированной неопределенности. Подготовьте диск для нескольких значений α в σ = 0.
sigma = 0;
alpha = [0.1,0.333,0.5];
diskmarginplot(alpha,sigma,'disk')
Как описано в Анализе Устойчивости с Использованием Полей Диска, для данного, самого большого диска неопределенности F, для которого система с обратной связью feedback(L*F,1) остается стабильным, может быть интерпретирована как область исключения, в которую не может войти кривая Найквиста L. Для любого значения и значения, диск исключения содержит критическую точку (-1,0) и является касательной к кривой Найквиста. Наклон регулирует размер и положение тангенциальных дисков. Можно использовать diskmarginplot визуализировать эти исключающие диски и наложить их на кривую Найквиста L.
Вычислите дисковые погрешности усиления для системы, используя три различных значения наклона, один из которых соответствует большему увеличению усиления, чем уменьшение (
L = tf(25,[1 10 10 10]); DMdec = diskmargin(L,-2); DGMdec = DMdec.GainMargin; DM = diskmargin(L,0); DGM = DM.GainMargin; DMinc = diskmargin(L,2); DGMinc= DMinc.GainMargin;
Чтобы просмотреть соответствующие области исключения, постройте график Годографов Найквиста L и удерживайте рисунок. Затем используйте diskmarginplot с 'nyquist' флаг для добавления областей исключения к графику.
nyquist(L) hold on diskmarginplot([DGMdec;DGM;DGMinc],'nyquist') hold off
![Figure contains an axes. The axes contains 9 objects of type line, patch. These objects represent L, DGM = [0.401,1.37], DPM = 29.1, DGM = [0.627,1.59], DPM = 25.8, DGM = [0.772,1.72], DPM = 21.](../../examples/robust/win64/NyquistPlotOfExclusionDiskExample_01.png)
Как увеличения от -2 до 2, диски перемещаются вправо, и каждый диск обеспечивает более низкие оценки классического усиления и запасов по фазе.
Постройте график полей диска как функции частоты системы со следующей характеристикой разомкнутого контура.
L = tf(25,[1 10 10 10]);
Для графика задайте следующие атрибуты:
Частотные модули: Гц
Запасы по амплитуде по журналу шкале, в абсолютных модулях
Сетка включена
opts = diskmarginoptions; opts.FreqUnits = 'Hz'; opts.MagScale = 'log'; opts.MagUnits = 'abs'; opts.grid = 'on'; diskmarginplot(L,opts)
L - Разомкнутый контурРазомкнутый контур, заданная как динамическая системная модель. L может быть SISO или MIMO, пока это имеет одинаковое количество входов и выходов. diskmarginplot строит графики дискового коэффициента усиления и запасов по фазе для системы с обратной отрицательной связью с обратной связью feedback(L,eye(N)).
Для построения графика полей системы положительной обратной связи feedback(L,eye(N),+1), использовать diskmargin(-L).
Если L - модель неопределенного пространства состояний (uss или genss с неопределенными блоками), затем diskmarginplot строит графики полей случайных выборок L. Чтобы визуализировать наихудшие запасы устойчивости неопределенной системы, используйте wcdiskmarginplot.
Если L является моделью данных частотной характеристики (такой как frd), затем diskmarginplot строит графики полей на каждой частоте, представленной в модели.
Если L является массивом моделей, тогда diskmarginplot Строит графики полей для всех моделей массива на одной оси и в одном стиле линии.
sigma - ПерекосПерекос области неопределенности, используемой для вычисления запасов устойчивости, заданный как действительный скаляр или вектор (для diskmarginplot(alpha,sigma) только графики).
Этот параметр смещает неопределенность, используемую для моделирования изменений усиления и фазы в сторону увеличения или уменьшения усиления.
Значение по умолчанию sigma = 0 использует сбалансированную модель изменения усиления в области значений [gmin,gmax], с gmin = 1/gmax.
Положительное sigma использует модель с большим увеличением усиления, чем уменьшением (gmin > 1/gmax).
Отрицательные sigma использует модель с большим уменьшением усиления, чем увеличением (gmin < 1/gmax).
Для получения более подробной информации о том, как выбор sigma влияет на расчет запаса, см. «Анализ устойчивости с использованием полей на диске».
diskmargin(L,sigma) СинтаксисПри построении графика запасов по амплитуде динамической системы от частоты используйте sigma по умолчанию = 0, чтобы получить объективные оценки усиления и запасов по фазе. Для sigma = 0, дисковый запас по амплитуде на каждой частоте ± GM, где GM - значение, показанное на графике в дБ .
Если вы использовали diskmargin для получения дисковых полей с некоторыми конкретными sigma, можно использовать этот синтаксис, чтобы увидеть частотную зависимость полей при этом sigma значение. Для sigma ≠ 0 нанесенное на график значение GM = min(gmax,1/max(0,gmin)). Другими словами, график показывает наибольшую величину изменения усиления [1/GM,GM] который помещается в пределах дискового запаса по амплитуде [gmin,gmax] системы на заданном sigma.
Для получения синтаксиса diskmarginplot(L,sigma), перекос sigma должно быть скаляром.
diskmargin(alpha,sigma) СинтаксисВ синтаксисе diskmargin(alpha,sigma), графики функций диск неопределенности, параметризованный значениями alpha и sigma (см. Анализ устойчивости с использованием полей диска). Для преобразования дисковых запасов по амплитуде и alpha, sigma параметризация, использование dm2gm и gm2dm. Для этого синтаксиса, diskmarginplot применяет отношение alpha*abs(1+sigma) < 2.
Для этого синтаксиса, перекос sigma может быть вектором, позволяющим сравнивать несколько дисков на одном графике. Если alpha является скаляром и sigma является вектором, затем на графике показаны диски, соответствующие парам alpha,sigma_k для каждой записи в sigma. Если оба alpha и sigma являются векторами, затем на графике показаны диски для пар alpha1,sigma1;...;alphaN,sigmaN.
w - Частоты{wmin,wmax} | векторЧастоты, на которых можно построить запасы устойчивости, заданные как массив ячеек {wmin,wmax} или как вектор значений частоты.
Если w - массив ячеек вида {wmin,wmax}, затем на графике показаны поля на частотах между wmin и wmax.
Если w является вектором частот, тогда график показывает поля на каждой заданной частоте. Для примера используйте logspace чтобы сгенерировать вектор-строку с логарифмически разнесенными значениями частоты.
Задайте частоты в единицах рада TimeUnit, где TimeUnit является TimeUnit свойство L.
opts - Опции графикаdiskmarginplot набор опцийОпции графика, заданные как diskmarginplot набор опций, который вы создаете с diskmarginoptions. Элементы, которые можно настроить, включают заголовок графика, метки осей и сетки.
DGM - Дисковый запас по амплитудеДисковый запас по амплитуде, заданный как скаляр, двухэлементный вектор вида [gmin,gmax], или двухколоночная матрица вида [gmin1,gmax1; ...; gminN,gmaxN].
Используйте двухэлементный вектор, DGM = [gmin,gmax] для построения графика допустимой области значений одновременных изменений усиления и фазы, соответствующего дисковому запасу по амплитуде [gmin,gmax]. Можно получить [gmin,gmax] в GainMargin поле структур output diskmargin команда. Можно также получить [gmin,gmax] от классического усиления и запасов по фазе с использованием getDGM.
Использование скалярного DGM эквивалентно заданию симметричного запаса по амплитуде [1/DGM,DGM].
Чтобы показать области значений нескольких дисковых запасов по амплитуде на том же графике, используйте DGM = [gmin1,gmax1;...;gminN,gmaxN]. Для симметричных запасов по амплитуде формы [1/gmax,gmax]можно использовать вектор-столбец формы [gmax1;gmax2;...;gmaxN].
alpha - Размер усиления и изменения фазыРазмер смоделированных изменений усиления и фазы, заданный как скаляр или вектор. Дисковый анализ запасов по амплитуде моделирует коэффициент усиления и изменение фазы как мультипликативную F неопределенности, которая является диском значений, содержащих F = 1, соответствующих номинальному значению системы. Диск параметризируется alpha, который устанавливает размер диска, и sigma, который смещает изменение усиления к увеличению или уменьшению усиления. (Для получения дополнительной информации об этой модели см. Анализ устойчивости с использованием полей диска.)
diskmarginplot позволяет вам построить график дискового F или области изменений усиления и фазы, представленных конкретными alpha, sigma пар. Для получения синтаксиса diskmarginplot(alpha,sigma), размер диска alpha может быть вектором. Если alpha является вектором и sigma является скаляром, тогда на графике показаны области, соответствующие парам alpha_k,sigma для каждой записи в alpha. Если оба alpha и sigma являются векторами, затем на графике показаны области для пар alpha1,sigma1;...;alphaN,sigmaN.
diskmarginplot применяет отношение alpha*abs(1+sigma) < 2. Для преобразования дисковых запасов по амплитуде и alpha, sigma параметризация, использование dm2gm и gm2dm.
AX - указатель осейaxes | объекта UIAxes объектУказатель на ось, заданный как axes объект или UIaxes объект. Используйте этот аргумент для задания осей при создании приложений в Develope Apps Using App Designer.
[1] Сейлер, Питер, Эндрю Паккард и Паскаль Гахинет. «Введение в области дисковых полей [примечания к лекциям]». Журнал IEEE Control Systems Magazine 40, № 5 (октябрь 2020): 78-95.
diskmargin | diskmarginoptions | getDGM | gm2dm | umargin | wcdiskmarginplot