Моделируйте неопределенность усиления и фазы
Используйте umargin управляйте проектируемым блоком, чтобы смоделировать изменения коэффициента усиления и фазы в циклах обратной связи. Моделирование изменений усиления и фазы в вашей системе позволяет вам проверить запасы устойчивости во время анализа робастности или применить их во время устойчивого проектирования контроллера.
Чтобы добавить неопределенность усиления и фазы в цикл обратной связи, вы включаете umargin блокируется в неопределенное пространство состояний (uss) модель системы с обратной связью. umargin - блок системы управления SISO, представляющий изменение усиления и фазы в одном местоположении в одном цикле обратной связи. Чтобы смоделировать неопределенность усиления и фазы в системах обратной связи MIMO, вставьте отдельную umargin объект в каждом месте в системе, в котором вы хотите ввести неопределенность усиления и фазы.
umargin моделирует изменения усиления и фазы как коэффициент F умножения L отклика без разомкнутого контура. Этот коэффициент принимает значения в диске с центром на действительной оси и содержащем F = 1. Этот диск задается его пересечением DGM = [gmin,gmax] с действительной осью, которая представляет относительную величину изменения усиления вокруг номинального значения F = 1. Чтобы задать как неопределенность усиления, так и фазы, сначала используйте getDGM для получения DGM значение, которое описывает диск, который захватывает и указанный диапазон усиления, и области значений фаз. Для получения дополнительной информации о дисковой модели неопределенности см. Алгоритмы.
Когда у вас есть uss модель, содержащая umargin Система управления блоков можно выполнить анализ робастности и наихудшего случая, чтобы изучить, как изменение усиления и фазы влияет на реакцию системы. Для образца используйте robstab и robgain анализ устойчивой устойчивости и устойчивой эффективности системы с неопределенностью усиления и фазы. Использовать wcgain и wcsigmaplot изучить наихудшие отклики системы.
Требование устойчивой устойчивости для системы с обратной связью с umargin неопределенность усиления и фазы эквивалентна применению дискового запаса по амплитуде [gmin,gmax] и соответствующий запас по фазе. Поэтому можно использовать umargin блоки для обеспечения соответствующих полей диска при разработке устойчивых контроллеров с musyn.
F = umargin(name,DGM)DGM = [gmin,gmax] с gmin < 1 и gmax > 1. Коэффициент усиления, смоделированный F изменяется в этой области значений для фазы, удерживаемой на его номинальном значении. Когда у вас есть неопределенность усиления и фазы, используйте getDGM для поиска соответствующей DGM. Этот синтаксис также устанавливает Name свойство F.
F = umargin(name,GM)umargin(name,[1/GM,GM]). Этот синтаксис задает коэффициент усиления, который может увеличиться или уменьшиться на множитель GM при отсутствии фазы неопределенности. Соответствующее количество неопределенности фазы определяется дисковой моделью неопределенности, которая umargin использует (см. Алгоритмы).
F = umargin(___,Name,Value)F использование пар "имя-значение". Для примера, F = umargin('F',[0.8,1.4],'InputName','u0','OutputName','u') создает umargin Блок и устанавливает имена входа и выхода для использования с connect. Заключайте каждое имя свойства в кавычки.
Многие функции, которые работают с числовыми моделями LTI, также работают с неопределенными блоками системы управления, такими как umargin. Они включают функции соединения моделей, такие как connect и feedback, и функции линейного анализа, такие как bode и stepinfo. Некоторые функции, которые генерируют графики, такие как bode и step, постройте случайные выборки неопределенной модели, чтобы дать вам ощущение распределения неопределенной динамики. Однако при использовании этих команд для возврата данных они работают только с номинальным значением системы. Следующие списки содержат репрезентативное подмножество функций, с которыми можно использовать umargin модели.
umargin моделирует изменения коэффициента усиления и фазы в отдельном канале обратной связи как частотно-зависимый множительный коэффициент F (s), умножающий номинальную L отклика без разомкнутого контура (s), так что возмущенная характеристика является L (s) F (s). Коэффициент F (s) параметризован:
В этой модели,
δ (s) является динамической неопределенностью с ограничением по усилению, нормированной так, что она всегда изменяется внутри единичного диска (||<reservedrangesplaceholder0>||∞ < 1).
ɑ устанавливает величину усиления и изменения фазы, смоделированные F. Для фиксированных σ параметр ɑ управляет размером диска. Для ɑ = 0 мультипликативный коэффициент равен 1, соответствующий номинальной L.
σ, называемое skew, смещает смоделированную неопределенность в сторону увеличения или уменьшения усиления.
Коэффициент F принимает значения в диске с центром на действительной оси и содержащем номинальное значение F = 1. Диск характеризуется своей точкой пересечения DGM = [gmin,gmax] с действительной осью. gmin < 1 и gmin > 1 - минимальные и максимальные относительные изменения в усилении, моделируемые F, в номинальной фазе. Фаза неопределенность, смоделированная F, является областью значений DPM = [pmin,pmax] значений фазы при номинальном усилении (|<reservedrangesplaceholder1>| = 1). Например, на следующем графике правая сторона показывает дисковое F, которое пересекает действительную ось в интервале [0.71.1.4]. Левая сторона показывает, что этот диск моделирует изменение усиления ± 3 дБ и изменение фазы ± 19 °.
F = umargin('F',1.4125)
plot(F)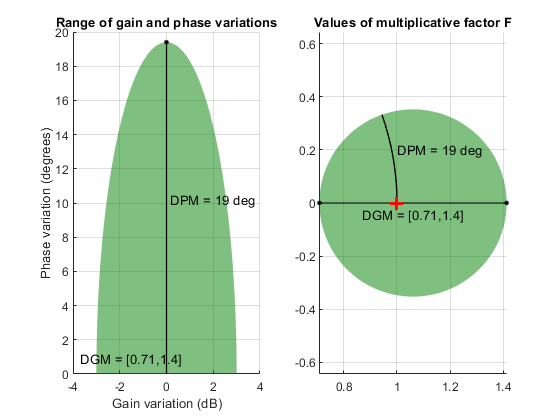
Когда вы создаете umargin блок, вы задаете величину неопределенности путем определения DGM. Использовать getDGM чтобы переместить определенные величины изменений усиления и фазы в подходящую DGM область значений, который захватывает эти изменения. Для получения дополнительной информации о модели неопределенности, используемой umargin, см. Анализ устойчивости с использованием полей диска.