Поля диска определяют количество устойчивости системы с обратной связью против изменений усиления или фазы в отклике без разомкнутого контура. В дисковых вычислениях запаса программное обеспечение моделирует такие изменения, как дискообразная мультипликативная неопределенность в передаточной функции без разомкнутого контура. Этот disk margin измеряет, какую неопределенность может терпеть цикл, прежде чем идти нестабильно.
Эта сумма неопределенности соответствует минимальным запасам по усилению и фазе. Дисковое DGM запаса по амплитуде является величиной, на которую коэффициент усиления цикла может увеличиваться или уменьшаться без потери устойчивости в абсолютных модулях. Основанный на диске запас по фазе DPM является величиной, на которую фаза цикла может увеличиваться или уменьшаться без потери устойчивости, в степенях. Эти дисковые поля учитывают все частоты и циклические взаимодействия. Поэтому дисковый анализ запаса обеспечивает более сильную гарантию устойчивости, чем классические запасы по усилению и фазе.
Robust Control Toolbox™ предоставляет инструменты для:
Анализируйте устойчивость системы при изменениях коэффициента усиления и фазы. Использовать diskmargin вычисление дискового коэффициента усиления и запасов по фазе циклов обратной связи SISO и MIMO.
Моделируйте неопределенность усиления и фазы. Используйте umargin система управления для анализа эффекта усиления и неопределенности на производительность и стабильность системы.
Оба umargin и diskmargin представляют изменение усиления и фазы как мультипликативный комплексный коэффициент F (s), заменяя номинальный разомкнутый ответ L (s) на L (s) *F (ы). Коэффициент F принимает значения на диске, который включает номинальное значение F = 1. Этот мультипликативный коэффициент моделирует как изменение усиления, так и изменения фазы. Например, на следующем графике показан один такой диск в комплексной плоскости.
DGM = [0.6,1.7];
diskmarginplot(DGM,'disk')
Значения в этом диске охватывают относительные изменения только для усиления в области значений DGM = [0,6,1,7], или ± 4 дБ. Они также представляют абсолютные изменения DPM = [-29,29], или ± 29 °. Полагайте, что следующая система с обратной связью, с номинальным циклом передают обратная связь модуля и L.

Если этот цикл обратной связи остается стабильным для всех значений F на диске, показанном на предыдущем графике, то дисковый запас по амплитуде L как минимум DGM, и дисковый запас по фазе, по меньшей мере DPM.
И умаргин, и дискмаргин моделируют усиление и фазу неопределенность с семейством дисков, описанных двумя параметрами, α и Для систем SISO диск параметризируется:
В этой модели,
.r- нормированная неопределенность (произвольное комплексное число в единичном диске |δ| < 1).
α устанавливает величину усиления и изменения фазы, смоделированные F. Для фиксированного, параметр α управляет размером диска. Для α = 0 мультипликативный коэффициент равен 1, соответствующий номинальному L.
, называемый перекосом, смещает смоделированную неопределенность в сторону увеличения или уменьшения усиления.
Каждая пара α, в, соответствует диску, который моделирует конкретную область значений вариаций усиления DGM = [gmin, gmax], заданный точками, где диск перехватывает действительную (x) ось. Соответствующее изменение фазы DPM определяется углом между действительной осью и линией через источник координат и тангенс к диску. Таким образом Вы можете описать смоделированный набор выгоды и изменений фазы полностью или двумя значениями α,σ или двумя значениями DGM = [gmin, gmax]. .r= 0 моделирует сбалансированное изменение коэффициента усиления с [gmin, gmax] таким, что gmin = 1/gmax. Когда и < 0, тогда F представляет большее уменьшение усиления, чем увеличение (gmin < 1/gmax). И, наоборот, ', 0' представляет большое увеличение усиления, чем уменьшение. Например, рассмотрим диски, параметризованные α = 0,5 и тремя различными перекосами,
diskmarginplot(0.5,[-2 0 2],'disk')
Каждый α,σ пара соответствует диску, который моделирует другой диапазон изменений выгоды DGM = [gmin, gmax]. Исследуйте изменения коэффициента усиления, которые соответствуют каждому из этих трех дисков.
Ranges = dm2gm(0.5,[-2 0 2])
Ranges = 3×2
0.3333 1.4000
0.6000 1.6667
0.7143 3.0000
diskmarginplot(Ranges)
![Figure contains an axes. The axes with title Range of gain and phase variations contains 3 objects of type patch. These objects represent DGM = [0.333,1.4], DPM = 32.2, DGM = [0.6,1.67], DPM = 28.1, DGM = [0.714,3], DPM = 32.2.](../../examples/robust/win64/ModelingGainAndPhaseVariationsExample_04.png)
Уравновешенный диапазон и = 0 симметричен вокруг номинального значения, что позволяет усилению увеличиваться или уменьшаться в множителе около 1,67. Отрицательное значение, соответствует большему уменьшению усиления, чем увеличению, в то время как положительная
The umargin блок проекта управления использует эту модель, чтобы представлять неопределенность усиления и фазы в цикле обратной связи, задавая α и The diskmargin команда использует эту модель для вычисления дисковых коэффициентов усиления и запасов по фазе, как описано в следующем разделе.
Для передачи цикла L и заданного наклона, diskmargin команда находит самый большой размер диска α, при котором система с обратной связью feedback(L*F,1) является стабильным для всех значений F. Это значение α называется полем диска. Дисковый запас по амплитуде DGM и дисковый запас по фазе DPM - область значений изменений усиления и фазы, представленный соответствующим диском.
Для образца вычислите запас по диску и связанный с ним дисковый коэффициент усиления и запасов по фазе для передаточной функции SISO с помощью значения по умолчанию и 0.
sigma = 0; L = tf(25,[1 10 10 10]); DM = diskmargin(L,sigma); alpha = DM.DiskMargin
alpha = 0.4581
DGM = DM.GainMargin
DGM = 1×2
0.6273 1.5942
DPM = DM.PhaseMargin
DPM = 1×2
-25.8017 25.8017
Для этой системы уравновешенный (σ = 0) дисковый край α является приблизительно 0,46. Соответствующий дисковый запас по амплитуде DGM показывает, что система остается стабильной при относительных изменениях коэффициента усиления между приблизительно 0,63 и 1,6 или при изменениях фазы приблизительно ± 26 степеней. Этот результат устанавливает стабильность для всех значений F на диске :
diskmarginplot(DGM,'disk')
Запасы по амплитуде являются пересечением диска с действительной осью. Запас по фазе является самым большим углом между действительной осью и линией через источник тангенс к диску.
Комбинированные изменения коэффициента усиления и фазы
Область запасов по амплитуде DGM вы получаете от diskmargin предположим, что нет изменения фазы и запасов по фазе DPM предположим, что нет изменения усиления. На практике ваша система может испытывать одновременные изменения усиления и фазы. diskmarginplot позволяет вам визуализировать области значений одновременных изменений усиления и фазы, которые система может допустить.
diskmarginplot(DGM)

Затененная область показывает стабильную область значений комбинированных изменений усиления и фазы. Таким образом, например, без изменения фазы, система может терпеть полную область значений DGM изменения усиления, приблизительно от -4 дБ до 4 дБ. Если фазе позволяют изменяться ± на 17 степени или около того, допустимое изменение усиления падает до области значений от примерно -3 дБ до 3 дБ.
Поля диска и наклон
Области значений, показанные выше, вычисленные для σ = 0, представляют уравновешенное изменение выгоды, где gmin = 1 / gmax. Изменение перекоса может показать, является ли цикл более чувствительным к увеличению или уменьшению. Например, использование σ> 0 может показать, что обратная связь очень прочна, чтобы получить увеличение, потому что положительные σ модели больше увеличения выгоды, чем уменьшение. Этот результат, однако, мало говорит о робастности для уменьшения. Попробуйте вычислить дисковые коэффициенты усиления и запасов по фазе для L, смещая поля в сторону увеличения или уменьшения усиления.
DMdec = diskmargin(L,-2); DMinc = diskmargin(L,2); DGMdec = DMdec.GainMargin
DGMdec = 1×2
0.4013 1.3745
DGMinc = DMinc.GainMargin
DGMinc = 1×2
0.7717 1.7247
В совокупности эти результаты показывают, что в отсутствие изменения фазы стабильность сохраняется при относительных изменениях усиления между 0,4 и 1,72. Чтобы увидеть, как запас по фазе зависит от этих вариаций усиления, постройте график стабильных областей значений изменений по усилению и фазе для каждой diskmargin результат.
diskmarginplot([DGMdec;DGM;DGMinc]) legend('\sigma = -2','\sigma = 0','\sigma = 2') title('Stable range of gain and phase variations')

Этот график показывает, что цикл обратной связи может переносить большие изменения фазы, когда коэффициент усиления уменьшается. Другими словами, стабильность цикла более чувствительна к увеличению усиления. Обратите внимание, что было бы вводящим в заблуждение просто взять наибольший отчетный запас по фазе (почти 30 степени для Действительно, это большое значение предсказывается небольшим увеличением усиления менее 3 дБ. Поскольку и коэффициент усиления, и фаза подвержены неопределенности в целом, важно обратить внимание на комбинированные изменения. Для примера график показывает, что, когда коэффициент усиления увеличений на 4 дБ, запас по фазе падает до менее 15 степеней. Напротив, он остается больше 30 степени, когда коэффициент усиления уменьшается на 4 дБ.
В заключение, изменение наклона и может дать более полную картину чувствительности к усилению и фазовой неопределенности. Если вы в основном не обеспокоены изменениями усиления в одном направлении (увеличение или уменьшение), не рекомендуется делать выводы из одного ненулевого значения Вместо этого используйте значение по умолчанию и = 0, чтобы получить объективные оценки усиления и запасов по фазе. При использовании ненулевых значений в, используйте как положительные, так и отрицательные значения, чтобы сравнить относительную чувствительность к увеличению усиления и уменьшению усиления.
Диск неопределенности в плоскости Найквиста
Требование устойчивой устойчивости для системы с обратной связью feedback(L*F,1) эквивалентно требованию, которое 1 + L*F ≠ 0. В плоскости Найквиста это требование становится L (j,) ≠ -1/F. Таким образом диск F для каждого значения σ определяет область исключения, в которую не входит кривая Найквиста, если стабильность с обратной связью сохранена. Все такие диски -1/F содержать критическую точку (-1,0) и касательны к кривой Найквиста. Наклон регулирует размер и положение тангенциальных дисков, как показано на следующем графике, который показывает области исключения для трех дисковых полей L, вычисленных выше. По мере увеличения, каждый диск обеспечивает более низкие оценки классического усиления и запасов по фазе.
nyquist(L) hold on diskmarginplot([DGMdec;DGM;DGMinc],'nyquist') p = findobj(gca,'type','patch'); legend(p,'\sigma = -2','\sigma = 0','\sigma = 2') hold off

Для получения дополнительной информации о интерпретации Nyquist диска неопределенности, смотрите Маржа диска и наименьшее дестабилизирующее возмущение.
Для систем MIMO модель применяет независимый диск неопределенности Fj к каждому каналу цикла, заданный как
Модель заменяет L разомкнутого цикла MIMO на L * F, где
Аналогично случаю SISO, запас диска является самым большим значением α, для которых система с обратной связью feedback(L*F,eye(N)) является стабильным для всех значений F. Может быть полезно учитывать независимые изменения сразу по всем каналам обратной связи, а также изменения в отдельных каналах. Поэтому, diskmargin позволяет вам вычислить:
Loop-at-a-time поля - максимальные допустимые изменения усиления (или изменения фазы) в каждом канале обратной связи, вычисленные со всеми другими циклами. Loop-at-a-time анализ эффективно устанавливает все δj равными 0 для всех каналов, кроме анализируемого канала.
Multiloop margins - максимально допустимые изменения усиления (или изменения фазы) во всех каналах обратной связи. Многоуровневые поля допускают независимые изменения во всех каналах обратной связи одновременно. Способность захватывать такие циклические взаимодействия является ключевым преимуществом дискового подхода по сравнению с классическим маржинальным анализом. Мультилупный анализ обычно приводит к меньшим запасам, чем циклический анализ за раз.
Для образца рассмотрим 2-канальную систему MIMO следующего рисунка.
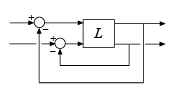
Для этой системы можно вычислить:
Максимально допустимые изменения усиления (или изменения фазы) в первом канале (первый системный вход в первый системный выход)
Максимально допустимые изменения усиления (или изменения фазы) во втором канале (второй системный вход во второй системный выход)
Максимально допустимые независимые изменения усиления (или изменения фазы) в обоих каналах одновременно.
Для получения дополнительной информации и примеров того, как получить эти поля цикла в момент времени и мультициклов, смотрите diskmargin.
В некоторых случаях запасы устойчивости могут варьироваться в зависимости от того, применяются ли изменения коэффициента усиления и фазы на входе объекта управления или на выходе объекта. diskmargin позволяет вычислять поля для изменений на входе, выходе или обоих одновременно. В целом, запасы для одновременных изменений входных и выходных параметров меньше, чем для входных или выходных, и обеспечивают более консервативную гарантию устойчивости. Рассмотрите систему с обратной связью SISO или MIMO следующей схемы.
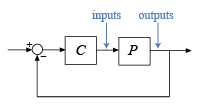
Вы можете вычислить поля диска на входах и выходах объекта следующим образом.
[DM,MM] = diskmargin(P*C) возвращает поля для изменений на выходах объекта.
[DM,MM] = diskmargin(C*P) возвращает поля для изменений на входах объекта управления.
MMIO = diskmargin(P,C) возвращает запас для одновременных изменений на выходах и входах объекта. При сравнении этого поля с полями в входах или выходах используйте 2*MMIO.Diskmargin, для расчета одновременных возмущений, приложенных как к входам, так и к выходам.
В целом, запасы по усилению и фазе варьируются по частоте. Это изменение связано с изменением частоты разомкнутой характеристики L: Для каждого частотного ω существует разное самое большое α (ω), такое что I L + jω (F) является инвертируемым для всех значений F в диске. Это значение является первым α (ω), для которого полюс с обратной связью пересекает ось jω на частотной ω, становясь нестабильным.
Когда α запаса диска изменяется в зависимости от частоты, изменяется и соответствующая допустимая область значений изменений усиления или фазы. Построение графиков этих дисковых полей как функции частоты предоставляет информацию о полосах со слабыми полями.
L = tf(25,[1 10 10 10]); diskmarginplot(L)
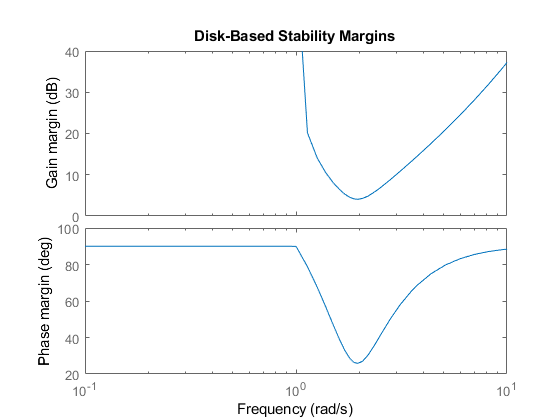
Поля диска, возвращенные diskmargin являются минимальными такими значениями по всем частотам. Щелкните правой кнопкой мыши по графику, сгенерированному diskmarginplot для всплывающей подсказки с информацией об этих значениях.
Запас диска вычисляется путем применения неопределенности к номинальной передаточной L цикла и вычисления того, насколько велика может быть эта неопределенность, при сохранении устойчивости замкнутого цикла. Если L передачи цикла сама по себе является неопределенной системой, то запас диска также изменяется как функция от других неопределенностей в системе. Это worst-case disk margin - наименьший запас диска, который возникает в областях значений неопределенностей, смоделированных в L. Это также минимальный гарантированный запас в области значений неопределенностей.
Вычисление наихудших дисковых полей неопределенной системы с помощью wcdiskmargin. Эта функция оценивает поля диска в худшем случае и соответствующий коэффициент усиления и запасов по фазе в худшем случае для как цикла, так и мультицикл изменений. Функция также возвращает возмущение в худшем случае, комбинацию неопределенных элементов в L, которая приводит к самым слабым запасам. Вы можете визуализировать наихудшие дисковые поля сwcdiskmarginplot.
systune или Control System TunerИнструменты настройки системы управления в Control System Toolbox™ позволяют вам задать целевые запасы по усилению и фазе для циклов в настроенной системе. Цели настройки TuningGoal.Margins (для настройки командной строки с systune) и Margins Goal (для настройки с помощью Control System Tuner) используют дисковые поля. Таким образом, когда вы задаете независимые запасы по фазе и GM усиления и PM для настройки, программное обеспечение выбирает наименьший α, который применяет оба значения. Эта α описывается следующим образом:
При применении этого значения α программное обеспечение настройки принимает σ = 0.
Визуализация маржинальных целей с помощью viewGoal или Control System Tuner tuning-target графики эквивалентны diskmarginplot(L), где L - настроенный ответ разомкнутого контура.
musynКогда вы выполняете устойчивую настройку контроллера с musyn, можно смоделировать изменения усиления и фазы непосредственно в вашей системе, используя umargin. Затем, выполняя устойчивое проектирование контроллера с musyn обеспечивает устойчивую стабильность для смоделированной области значений изменений усиления и фазы. Этот подход полезен, потому что он позволяет вам изучить эффекты ожидаемых изменений усиления и фазы на всех аспектах производительности системы с помощью той же модели, которую вы используете для настройки. Для получения примера смотрите Робастный Контроллер для Вращающегося Спутника.
Недостатком этого подхода является то, что musyn не только обеспечивает устойчивую стабильность во всем смоделированной области значений неопределенностей. Он также пытается обеспечить устойчивую эффективность. (См. Robust Performance Measure for Mu-Synthesis.) Достижение этого более строгого требования обычно невозможно или приводит к недопустимому ухудшению номинальной эффективности. Таким образом, вам может потребоваться уменьшить смоделированные изменения усиления и фазы, чтобы поддерживать разумную эффективность. systune и Control System Tuner не имеют этого недостатка, потому что они обрабатывают цели запаса независимо от каких-либо целей эффективности.
[1] Блайт, Джеймс Д., Р. Лейн Дэйли и Дагфинн Гангсаас. «Практический проект закона о контроле для самолетов с использованием многопараметрических методов». Международный журнал контроля 59, № 1 (январь 1994 года): 93-137. https://doi.org/10.1080/00207179408923071.
[2] Сейлер, Питер, Эндрю Паккард и Паскаль Гахинет. «Введение в области дисковых полей [примечания к лекциям]». Журнал IEEE Control Systems Magazine 40, № 5 (октябрь 2020): 78-95.
diskmargin | diskmarginplot | umargin | wcdiskmargin