Вычислите L 2 норму системы непрерывного времени в обратной связи с системой дискретного времени
[gaml,gamu] = sdhinfnorm(sdsys,k) [gaml,gamu] = sdhinfnorm(sdsys,k,delay) [gaml,gamu] = sdhinfnorm(sdsys,k,delay,tol)
[gaml,gamu] = sdhinfnorm(sdsys,k) вычисляет L 2 вызванную норму объекта LTI в непрерывном времени, sdsys, в обратной связи с контроллером дискретного времени, k, соединенный через идеальный дискретизатор и удержание нулевого порядка (см. рисунок ниже). sdsys должна быть строго правильной, так что коэффициент усиления постоянной обратной связи должен быть нулем. Выходы, gamu и gaml, являются верхними и нижними границами индуцированной L 2 нормы выборочных данных системы с обратной связью.
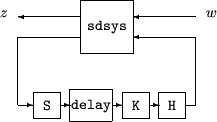
[gaml,gamu] = sdhinfnorm(sdsys,k,h,delay) включает в себя входной параметр delay. delay является неотрицательным целым числом, сопоставленным с количеством вычислительных задержек контроллера. Значение по умолчанию задержки 0.
[gaml,gamu] = sdhinfnorm(sdsys,k,h,delay,tol) включает в себя входной параметр, tol, что определяет различие между верхней и нижней границами при завершении поиска. Значение по умолчанию tol составляет 0,001.
Рассмотрим передаточную функцию без разомкнутого контура в непрерывном времени p = 30/s(s+30) и контроллер в непрерывном времени k = 4/(s+4). Система непрерывного времени с обратной связью имеет пиковую величину на частоте 1.
p = ss(tf(30,[1 30])*tf([1],[1 0]));
k = ss(tf(4,[1 4]));
cl = feedback(p,k);
norm(cl,'inf')
ans =
1
Первоначально контроллер должен быть реализован со скоростью дискретизации 1,5 Гц. Норма выборочных данных системы с обратной связью с контроллером дискретного времени составляет 1,0.
kd = c2d(k,0.75,'zoh');
[gu,gl] = sdhinfnorm([1; 1]*p*[1 1],-kd);
[gu gl]
ans =
3.7908 3.7929
Из-за большого различия в норме между системой с обратной связью с непрерывным временем и выборочными данными частота дискретизации контроллера увеличивается с 1,5 Гц до 5 Гц. Норма выборочных данных новой системы с обратной связью - 3,79.
kd = c2d(k,0.2,'zoh');
[gu,gl] = sdhinfnorm([1; 1]*p*[1 1],-kd);
[gu gl]
ans =
1.0044 1.0049
sdhinfnorm использует изменения формул, описанных в бумаге Бамье и Пирсона, для получения эквивалентной системы дискретного времени. (Эти изменения сделаны, чтобы улучшить численное обусловление алгоритмов.) Предварительный шаг состоит в том, чтобы определить, является ли норма системы непрерывного времени в течение одного периода дискретизации без управления меньше заданного значения. Это требует поиска и является, в вычислительном отношении, относительно дорогим шагом.
Bamieh, B.A., and J.B. Pearson, «A General Среды for Linear Periodic Systems with Applications to Выборочных данных Control», IEEE Transactions on Automatic Control, Vol. AC-37, 1992, pp. 418-435.