Вычислите H ∞ контроллер для системы выборочных данных
[K,GAM]=sdhinfsyn(P,NMEAS,NCON) [K,GAM]=sdhinfsyn(P,NMEAS,NCON, KEY1,VALUE1,KEY2,VALUE2,...)
sdhinfsyn управляет системой LTI P в непрерывном времени с контроллером дискретного времени K. Объект непрерывного времени LTI P имеет реализацию в пространстве состояний, разделенную следующим образом:
где нарушение порядка в непрерывном времени входов войти через B 1, выходы от контроллера удерживаются постоянными между моментами дискретизации и входят через B 2, ошибки в непрерывном времени (чтобы храниться маленьким) соответствуют C 1 разделу, и измерения выхода, которые дискретизированы контроллером, соответствуют C 2 разделу. B 2 имеет размер столбца ncon и C 2 имеет размер строки nmeas. Обратите внимание, что матрица D должна быть нулем.
sdhinfsyn синтезирует LTI- контроллера в дискретном времени K достижение заданной нормы (по возможности) или нахождение минимально возможной нормы в пределах допуска TOLGAM.
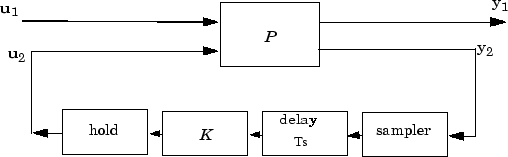
Подобно hinfsyn, функция sdhinfsyn использует итерацию γ. Учитывая высокое и низкое значение γ, GMAX и GMINМетод бисекции используется для итерации значения γ в попытке приблизиться к оптимальной схеме управления H ∞. Если GMAX = GMINПроверяется только одно γ значение. Критерий остановки для алгоритма бисекции требует, чтобы относительное различие между последним γ значением, которое не прошло, и последним γ значением, которое прошло, была меньше TOLGAM.
Входные параметры
P | Объект LTI |
NMEAS | Количество измерений, выводимых на контроллер |
NCON | Количество входов управления |
Необязательные входные параметры (KEY, VALUE) пары аналогичны hinfsyn, но с дополнительными KEY значения 'Ts' и 'DELAY'.
КЛЮЧ | ЗНАЧЕНИЕ | Значение |
|---|---|---|
| реальный | Начальная верхняя граница GAM (по умолчанию |
| реальный | Начальная нижняя граница GAM (по умолчанию = 0) |
| реальный | Относительная погрешность для GAM (по умолчанию = .01) |
| реальный | (По умолчанию = 1) шаг расчета контроллера, который будет разработан |
| целое число | (По умолчанию = 0) неотрицательное целое число, дающее количество периодов дискретизации для расчета управления |
|
| (По умолчанию) нет отображения командного окна или в командном окне отображается информация о прогрессе синтеза |
Выходные аргументы
K | H ∞ контроллер |
GAM | Конечное γ значение H ∞ достигнутых затрат |
sdhinfsyn использует изменение формул, описанную в бумаге Бамье и Пирсона [1], для получения эквивалентной системы дискретного времени. (Это делается, чтобы улучшить численное обусловление алгоритмов.) Предварительный шаг состоит в том, чтобы определить, является ли норма системы непрерывного времени в течение одного периода дискретизации без управления меньше, чем заданное γ-значение. Это требует поиска и является в вычислительном отношении относительно дорогим шагом.
[1] Bamieh, B.A., and J.B. Pearson, «A General Framework for Linear Periodic Systems with Applications to Sampled-Data Control», IEEE Transactions on Automatic Control., vol. AC-37, 1992, pp.
hinfsyn | norm | sdhinfnorm