Подгонка неопределенной модели к набору откликов LTI
usys = ucover(Parray,Pnom,ord)usys с номинальным значением Pnom и область значений поведения включает все отклики в массиве LTI Parray. Неопределенная структура модели имеет вид , где:
И это a ultidyn объект, который представляет неопределенную динамику с единичным пиковым усилением.
W является стабильным, минимально-фазовым формирующим фильтром порядка ord который корректирует величину неопределенности на каждой частоте. Для Pnom MIMO, W является диагональным, с порядками диагональных элементов, заданными ord.
usys = ucover(Parray,Pnom,ord1,ord2,utype)utype.
utype = 'InputMult' - Входной мультипликативный вид, в котором usys = Pnom*(I + W1*Delta*W2)
utype = 'OutputMult' - Выводит мультипликативную форму, в которой usys = (I + W1*Delta*W2)*Pnom
utype = 'Additive' - Аддитивная форма, в которой usys = Pnom + W1*Delta*W2
Delta представляет неопределенную динамику с единичным пиковым усилением, и W1 и W2 являются диагональными, стабильными, минимально-фазовыми формирующими фильтрами с порядками, заданными ord1 и ord2, соответственно.
[ улучшает подгонку, используя начальные значения фильтра в usys,info] = ucover(Pnom,info_in,ord1,ord2)info результат. Поставка новых порядков ord1 и ord1 для W1 и W2. Когда вы пробуете другие порядки фильтра, чтобы улучшить результат, этот синтаксис ускоряет итерацию, позволяя вам повторно использовать ранее вычисленную информацию.
Подгонка неопределенной модели к массиву откликов LTI. Откликами могут быть, например, результаты нескольких запусков, чтобы получить данные частотной характеристики от физической системы.
В данном примере сгенерируйте данные частотной характеристики путем создания массива моделей LTI и дискретизации частотной характеристики этих моделей.
Pnom = tf(2,[1 -2]); p1 = Pnom*tf(1,[.06 1]); p2 = Pnom*tf([-.02 1],[.02 1]); p3 = Pnom*tf(50^2,[1 2*.1*50 50^2]); array = stack(1,p1,p2,p3); Parray = frd(array,logspace(-1,3,60));
Данные частотной характеристики в Parray представляет три отдельных эксперимента по сбору данных в системе.
Постройте график относительных погрешностей между номинальной характеристикой объекта управления и тремя моделями в массиве LTI.
relerr = (Pnom-Parray)/Pnom; bodemag(relerr)
Если вы используете мультипликативную структуру модели неопределенности, необходимо, чтобы величина формирующего фильтра соответствовала максимальной относительной погрешности на каждой частоте. Используйте это требование, чтобы помочь выбрать порядок формирования фильтра. Сначала попробуйте фильтр формирования первого порядка.
[P,Info] = ucover(Parray,Pnom,1);
P является неопределенным пространством состояний (uss) модель, которая захватывает неопределенность как ultidyn блок неопределенной динамики.
P.Uncertainty
ans = struct with fields:
Parray_InputMultDelta: [1x1 ultidyn]
The Info структура содержит другую информацию о подгонке, включая полученный фильтр формирования, Info.W1. Постройте график отклика, чтобы увидеть, насколько хорошо формирующий фильтр соответствует относительным погрешностям.
W = Info.W1; bodemag(relerr,'b--',W,'r',{0.1,1000});
График показывает, что фильтр W является слишком консервативным и превышает максимальную относительную погрешность на большинстве частот. Чтобы получить более плотную подгонку, перезапустите функцию с помощью фильтра четвертого порядка.
[P,Info] = ucover(Parray,Pnom,4);
Рассчитать подгонку можно путем построения графика величины Боде.
W = Info.W1; bodemag(relerr,'b--',W,'r',{0.1,1000});
Этот график показывает, что для фильтра четвертого порядка, величина W тесно соответствует самой большой ошибке, получая минимальную неопределенность, которая захватывает все изменения.
ucover подходит для характеристик моделей LTI в Parray путем моделирования погрешностей между Parray и номинальный ответ Pnom как неопределенность в динамике системы. Чтобы смоделировать частотное распределение этой немоделированной динамики, ucover измеряет разрыв между Pnom и Parray на каждой частоте в сетке и выбирает формирующие фильтры, величина которых аппроксимирует максимальную погрешность.
Чтобы спроектировать минимально-фазовые формирующие фильтры W1 и W2, ucover команда выполняет два шага:
Вычислите оптимальные значения W1 и W2 на частотной сетке.
Подгонка W1 и W2 значений с динамическими фильтрами заданных порядков с помощью fitmagfrd.
Структура модели который вы получаете используя usys = ucover(Parray,Pnom,ord) соответствует W1 = W и W2 = 1.
Например, следующий рисунок показывает относительный промежуток между номинальным откликом и шестью откликами LTI, окаймленными с помощью формирующего фильтра второго порядка и фильтра четвертого порядка.
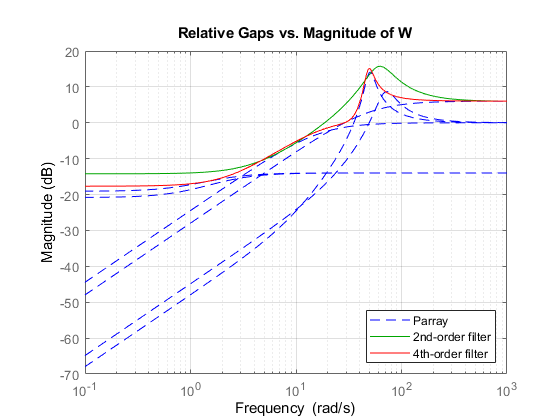
Если вы используете синтаксис одного фильтра usys = ucover(Parray,Pnom,ord), программное обеспечение устанавливает неопределенность на W*Delta, где Delta является ultidyn объект, который представляет неопределенную динамику с единичным усилением. Поэтому величина неопределенности на каждой частоте задается величиной W и тесно отслеживает зазор между Pnom и Parray. На приведенном выше рисунке фильтр четвертого порядка отслеживает максимальную погрешность более тесно и, следовательно, приводит к менее консервативной оценке неопределенности.