bandpass

Полосно-пропускающие сигналы

Свернуть все на странице

Синтаксис

y = bandpass(x,wpass)
y = bandpass(x,fpass,fs)
y = bandpass(xt,fpass)
y = bandpass(___,Name,Value)
[y,d] = bandpass(___)
bandpass(___)

Описание

y = bandpass(x,wpass) фильтрует входной сигнал x использование полосно-пропускающего фильтра с частотой полосы пропускания области значений заданной двухэлементным вектором wpass и выражены в нормированных модулях π рад/выборка. bandpass использует фильтр минимального порядка с затуханием в полосе задерживания 60 дБ и компенсирует задержку, введенную фильтром. Если x является матрицей, функция фильтрует каждый столбец независимо.

пример

y = bandpass(x,fpass,fs) задает, что x был дискретизирован со скоростью fs герц. Двухэлементный вектор fpass задает область значений частот полосы пропускания фильтра в hertz.

y = bandpass(xt,fpass) bandpass - фильтрация данных в xt timetable использование фильтра с частотой полосы пропускания области значений заданной в hertz двухэлементным вектором fpass. Функция независимо фильтрует все переменные в расписании и все столбцы внутри каждой переменной.

пример

y = bandpass(___,Name,Value) задает дополнительные опции для любого из предыдущих синтаксисов, используя аргументы пары "имя-значение". Можно изменить затухание в полосе задерживания, крутизну полосы переходов и тип импульсной характеристики фильтра.

пример

[y,d] = bandpass(___) также возвращает digitalFilter d объекта используется для фильтрации входов.

bandpass(___) без выходных аргументов строит график входного сигнала и накладывает отфильтрованный сигнал.

Примеры

свернуть все

Открыть Live Script

Создайте сигнал, дискретизированный с частотой 1 кГц в течение 1 секунды. Сигнал содержит три тональных сигнала, один с частотой 50 Гц, другой с частотой 150 Гц и третий с частотой 250 Гц. Оба высокочастотных и низкочастотных тональных сигнала имеют удвоенную амплитуду промежуточного тонального сигнала. Сигнал встроен в Гауссов белый шум отклонения 1/100.

fs = 1e3;
t = 0:1/fs:1;
x = [2 1 2]*sin(2*pi*[50 150 250]'.*t) + randn(size(t))/10;

Полосу пропускания - фильтрация сигнала для удаления низкочастотных и высокочастотных тональных сигналов. Задайте частоты полосы пропускания 100 Гц и 200 Гц. Отображение исходных и фильтрованных сигналов, а также их спектров.

bandpass(x,[100 200],fs)

Figure contains 2 axes. Axes 1 with title Bandpass Filtering (Fpass = [100 200] Hz) contains 2 objects of type line. These objects represent Original, Filtered. Axes 2 contains 2 objects of type line. These objects represent Original, Filtered.

Открыть Live Script

Реализуйте базовый синтезатор цифровой музыки и используйте его для воспроизведения традиционной песни. Задайте частоту дискретизации 2 кГц. Постройте спектрограмму песни.

fs = 2e3;
t = 0:1/fs:0.3-1/fs;

l = [0 130.81 146.83 164.81 174.61 196.00 220 246.94];
m = [0 261.63 293.66 329.63 349.23 392.00 440 493.88];
h = [0 523.25 587.33 659.25 698.46 783.99 880 987.77];
note = @(f,g) [1 1 1]*sin(2*pi*[l(g) m(g) h(f)]'.*t);

mel = [3 2 1 2 3 3 3 0 2 2 2 0 3 5 5 0 3 2 1 2 3 3 3 3 2 2 3 2 1]+1;
acc = [3 0 5 0 3 0 3 3 2 0 2 2 3 0 5 5 3 0 5 0 3 3 3 0 2 2 3 0 1]+1;

song = [];
for kj = 1:length(mel)
    song = [song note(mel(kj),acc(kj)) zeros(1,0.01*fs)];
end
song = song/(max(abs(song))+0.1);

% To hear, type sound(song,fs)

pspectrum(song,fs,'spectrogram','TimeResolution',0.31, ...
    'OverlapPercent',0,'MinThreshold',-60)

Figure contains an axes. The axes with title Fres = 8.2798 Hz, Tres = 310 ms contains an object of type image.

Полосу пропускания - сигнал, чтобы отделить средний регистр от двух других. Задайте частоты полосы пропускания 230 Гц и 450 Гц. Постройте график исходных и фильтрованных сигналов во временных и частотных диапазонах.

pong = bandpass(song,[230 450],fs);

% To hear, type sound(pong,fs)

bandpass(song,[230 450],fs)

Figure contains 2 axes. Axes 1 with title Bandpass Filtering (Fpass = [230 450] Hz) contains 2 objects of type line. These objects represent Original, Filtered. Axes 2 contains 2 objects of type line. These objects represent Original, Filtered.

Постройте график спектрограммы среднего регистра.

figure
pspectrum(pong,fs,'spectrogram','TimeResolution',0.31, ...
    'OverlapPercent',0,'MinThreshold',-60)

Figure contains an axes. The axes with title Fres = 8.2798 Hz, Tres = 310 ms contains an object of type image.

Открыть Live Script

Фильтруйте белый шум, дискретизированный с частотой дискретизации 1 кГц, используя полосовой фильтр с бесконечной импульсной характеристикой с шириной полосы пропускания 100 Гц. Используйте различные значения крутизны. Постройте график спектров фильтрованных сигналов.

fs = 1000;
x = randn(20000,1);

[y1,d1] = bandpass(x,[ 50 150],fs,'ImpulseResponse','iir','Steepness',0.5);
[y2,d2] = bandpass(x,[200 300],fs,'ImpulseResponse','iir','Steepness',0.8);
[y3,d3] = bandpass(x,[350 450],fs,'ImpulseResponse','iir','Steepness',0.95);

pspectrum([y1 y2 y3],fs)
legend('Steepness = 0.5','Steepness = 0.8','Steepness = 0.95', ...
    'Location','south')

Figure contains an axes. The axes with title Fres = 976.801 mHz contains 3 objects of type line. These objects represent Steepness = 0.5, Steepness = 0.8, Steepness = 0.95.

Вычислите и постройте график частотных характеристик фильтров.

[h1,f] = freqz(d1,1024,fs);
[h2,~] = freqz(d2,1024,fs);
[h3,~] = freqz(d3,1024,fs);

plot(f,mag2db(abs([h1 h2 h3])))
legend('Steepness = 0.5','Steepness = 0.8','Steepness = 0.95', ...
    'Location','south')
ylim([-100 10])

Figure contains an axes. The axes contains 3 objects of type line. These objects represent Steepness = 0.5, Steepness = 0.8, Steepness = 0.95.

Сделать фильтры асимметричными путем определения различных значений крутизны на более низкой и высокой частотах полосы пропускания.

[y1,d1] = bandpass(x,[ 50 150],fs,'ImpulseResponse','iir','Steepness',[0.5 0.8]);
[y2,d2] = bandpass(x,[200 300],fs,'ImpulseResponse','iir','Steepness',[0.5 0.8]);
[y3,d3] = bandpass(x,[350 450],fs,'ImpulseResponse','iir','Steepness',[0.5 0.8]);

pspectrum([y1 y2 y3],fs)

Figure contains an axes. The axes with title Fres = 976.801 mHz contains 3 objects of type line.

Вычислите и постройте график частотных характеристик фильтров.

[h1,f] = freqz(d1,1024,fs);
[h2,~] = freqz(d2,1024,fs);
[h3,~] = freqz(d3,1024,fs);

plot(f,mag2db(abs([h1 h2 h3])))
ylim([-100 10])

Figure contains an axes. The axes contains 3 objects of type line.

Входные параметры

свернуть все

Входной сигнал, заданный как вектор или матрица.

Пример: sin(2*pi*(0:127)/16)+randn(1,128)/100 задает шумную синусоиду

Пример: [2 1].*sin(2*pi*(0:127)'./[16 64]) задает двухканальную синусоиду.

Типы данных: single | double
Поддержка комплексного числа: Да

Нормированная частота полосы пропускания области значений, заданная как двухэлементный вектор с элементами в интервале (0, 1).

Частотная область значений полосы пропускания, заданный как двухэлементный вектор с элементами в интервале (0, fs/2).

Частота дискретизации, заданная как положительный действительный скаляр.

Входное расписание. xt должен содержать увеличивающиеся, конечные и равномерно разнесенные строки типа duration в секундах.

Если расписание имеет отсутствующие или повторяющиеся точки времени, можно исправить его с помощью советов в разделе «Чистое расписание с пропущенными, повторяющимися или неоднородными временами».

Пример: timetable(seconds(0:4)',randn(5,1),randn(5,2)) содержит одноканальный случайный сигнал и двухканальный случайный сигнал, дискретизированный с частотой дискретизации 1 Гц в течение 4 секунд.

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

Пример: 'ImpulseResponse','iir','StopbandAttenuation',30 фильтрует вход с помощью БИХ минимального порядка, который ослабляет на 30 дБ частоты, меньшие fpass(1) и частоты, большие fpass(2).

Тип импульсной характеристики фильтра, заданный как разделенная разделенными запятой парами, состоящая из 'ImpulseResponse' и 'fir', 'iir', или 'auto'.

  • 'fir' - Функция проектирует фильтр с минимальным порядком, линейной фазой, конечной импульсной характеристикой (КИХ). Чтобы компенсировать задержку, функция добавляет к входному сигналу N/2 нули, где N является порядком фильтра. Функция затем фильтрует сигнал и удаляет первые N/2 выборки выхода.

    В этом случае входной сигнал должен быть как минимум в два раза длиннее фильтра, который соответствует спецификациям.

  • 'iir' - Функция проектирует фильтр с бесконечной импульсной характеристикой (БИХ) минимального порядка и использует filtfilt функция для выполнения фильтрации нулевой фазы и компенсации задержки фильтра.

    Если сигнал не по крайней мере в три раза длиннее фильтра, который соответствует спецификациям, функция проектирует фильтр с меньшим порядком и, следовательно, меньшей крутизной.

  • 'auto' - Функция проектирует конечная импульсная характеристика минимального порядка, если входной сигнал достаточно длинный, и БИХ минимального порядка в противном случае. В частности, функция следует этим шагам:

    • Вычислите минимальный порядок, в котором конечной импульсной характеристике фильтр должен соответствовать спецификациям. Если сигнал по крайней мере в два раза длиннее необходимого порядка фильтра, разработайте и используйте этот фильтр.

    • Если сигнал недостаточно длинный, вычислите минимальный порядок, в котором БИХ фильтр должен соответствовать спецификациям. Если сигнал по крайней мере в три раза длиннее необходимого порядка фильтра, разработайте и используйте этот фильтр.

    • Если сигнал недостаточно длинный, обрезайте до трети длину сигнала и спроектируйте БИХ этого порядка. Уменьшение порядка происходит за счет крутизны переходной полосы.

    • Отфильтруйте сигнал и компенсируйте задержку.

Крутизна переходной полосы, заданная как разделенная разделенными запятой парами, состоящая из 'Steepness' и скалярный или двухэлементный вектор с элементами в интервале [0,5, 1). Когда крутизна увеличивается, реакция фильтра приближается к идеальной полосно-пропускающей способности, но результирующая длина фильтра и вычислительные затраты операции фильтрации также увеличиваются. Для получения дополнительной информации смотрите Bandpass Filter Shipness.

Фильтрация затухания в полосе задерживания, заданная как разделенная запятой пара, состоящая из 'StopbandAttenuation' и a положительной скалярной величины в дБ.

Выходные аргументы

свернуть все

Отфильтрованный сигнал, возвращенный как вектор, матрица или расписание с теми же размерностями, что и вход.

Полосовой фильтр, используемый в операции фильтрации, возвращается как digitalFilter объект.

  • Использовать filter(d,x) для фильтрации сигнала x использование d.

  • Используйте FVTool, чтобы визуализировать ответ фильтра.

  • Использовать designfilt для редактирования или генерации цифрового фильтра на основе спецификаций частотной характеристики.

Подробнее о

свернуть все

Крутизна полосно-пропускающего фильтра

The 'Steepness' аргумент управляет шириной переходных областей фильтра. Чем меньше крутизна, тем шире переходная область. Чем выше крутизна, тем более узкая переходная область.

Чтобы интерпретировать крутизну фильтра, примите во внимание следующие определения:

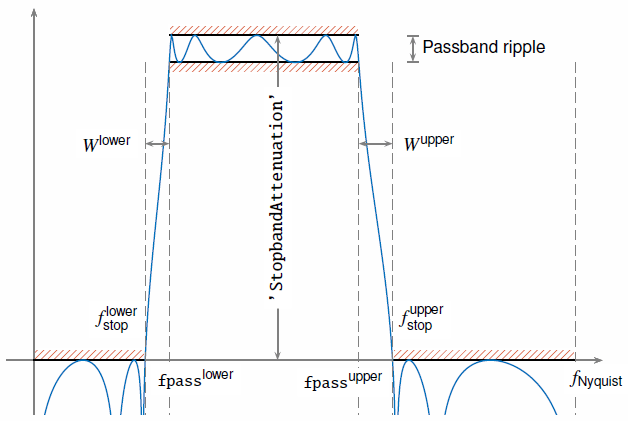
  • Частота Найквиста, f Найквиста, является самой высокой частотной составляющей сигнала, который может быть дискретизирован с заданной частотой без сглаживания. f Nyquist равен 1 (× π рад/сэмпл), когда входной сигнал не имеет информации о времени и fs/ 2 hertz, когда входной сигнал является расписанием или когда вы задаете частоту дискретизации.

  • Нижняя и верхняя частоты полосы остановки фильтра, f остановитеlower и f стопupper, являются частотами, ниже которых и выше которых ослабление равно или больше заданного значения 'StopbandAttenuation'.

  • Нижняя ширина перехода фильтра, Wlower, есть fpasslower - f упорlower, где fpasslower является первым элементом fpass.

  • Верхняя ширина перехода фильтра, Wupper, является f стопомupper – fpassupper, где fpassupper является вторым элементом fpass.

  • Большинство неидеальных фильтров также ослабляют входной сигнал через полосу пропускания. Максимальное значение этого частотно-зависимого ослабления называется неравномерностью в полосе пропускания. Каждый фильтр, используемый bandpass имеет неравномерность в полосе пропускания 0,1 дБ.

Чтобы контролировать ширину переходных полос, можно задать 'Steepness' как двухэлементный вектор, [slower, supper], или скаляр. Когда вы задаете 'Steepness' как вектор, функция:

  • Вычисляет нижнюю ширину перехода как

    Wlower = (1 – slower) × <reservedrangesplaceholder0>lower.

    • Когда первый элемент 'Steepness' равно 0,5, ширина перехода 50% от fpasslower.

    • Как первый элемент 'Steepness' приближается к 1, ширина перехода постепенно сужается, пока не достигает минимального значения 1% fpasslower.

  • Вычисляет верхнюю ширину перехода как

    Wupper = (1 – supper) × (f Найквист - fpassupper).

    • Когда второй элемент 'Steepness' равно 0,5, ширина перехода составляет 50% от (f Nyquist - fpassupper).

    • Как второй элемент 'Steepness' приближается к 1, ширина перехода постепенно сужается, пока не достигает минимального значения 1% (f Nyquist - fpassupper).

Когда вы задаете 'Steepness' в качестве скаляра функция проектирует фильтр с равными нижней и верхней ширинами перехода. Значение по умолчанию 'Steepness' составляет 0,85.

См. также

Приложения

Функции

Введенный в R2018a

Signal Processing Toolbox документация

Поддержка

Для просмотра документации необходимо авторизоваться на сайте