Параметрические методы моделирования находят параметры для математической модели, описывающей сигнал, систему или процесс. Эти методы используют известную информацию о системе, чтобы определить модель. Приложения для параметрического моделирования включают синтез речи и музыки, сжатие данных, спектральную оценку высокого разрешения, связь, производство и симуляцию.
Параметрические функции моделирования тулбокса работают с рациональной моделью передаточной функции. Учитывая соответствующую информацию о неизвестной системе (данные импульса или частотной характеристики, или входная и выходная последовательности), эти функции находят коэффициенты линейной системы, которая моделирует систему.
Одним из важных приложений параметрических функций моделирования является проект фильтров, которые имеют предписанную временную или частотную характеристику.
Вот сводные данные параметрических функций моделирования в этом тулбоксе.
Область | Функции | Описание |
|---|---|---|
Время | Сгенерируйте полнополюсные коэффициенты фильтра, которые моделируют последовательность входных данных с помощью алгоритма Левинсона-Дурбина. | |
Сгенерируйте полнополюсные коэффициенты фильтра, которые моделируют последовательность входных данных путем минимизации ошибки прямого предсказания. | ||
Сгенерируйте полнополюсные коэффициенты фильтра, которые моделируют последовательность входных данных путем минимизации ошибок предсказания вперед и назад. | ||
Сгенерируйте полнополюсные коэффициенты фильтра, которые моделируют последовательность входных данных с помощью оценки автокорреляционной функции. | ||
Линейное прогнозирующее кодирование. Сгенерируйте полнополюсный рекурсивный фильтр, импульсная характеристика которого совпадает с заданной последовательностью. | ||
Сгенерируйте БИХ, импульсная характеристика которого соответствует заданной последовательности. | ||
Найдите БИХ, выход которого, заданный как заданная входная последовательность, соответствует заданной выходной последовательности. | ||
Частота | Сгенерируйте коэффициенты цифрового или аналогового фильтра по данным комплексной частотной характеристики. |
lpc, prony, и stmcb функции находят коэффициенты цифровой рациональной передаточной функции, которая аппроксимирует заданную импульсную характеристику временной области. Алгоритмы различаются сложностью и точностью полученной модели.
Моделирование линейного предсказания принимает, что каждая выходная выборка сигнала, x(k), является линейной комбинацией прошлого n выходы (то есть они могут быть линейно предсказаны из этих выходов), и что коэффициенты являются постоянными от выборки к выборке:
Система координат nПолнополюсная модель сигнала I-го порядка x является
a = lpc(x,n)
Чтобы проиллюстрировать lpc, создайте сигнал расчета, который является импульсной характеристикой полнополюсного фильтра с аддитивным белым шумом:
x = impz(1,[1 0.1 0.1 0.1 0.1],10) + randn(10,1)/10;
Коэффициенты для полнополюсного фильтра четвертого порядка, который моделирует систему,
a = lpc(x,4)
lpc первые вызовы xcorr найти смещенную оценку корреляционной функции x, а затем использует рекурсию Левинсона-Дурбина, реализованную в levinson функция, чтобы найти коэффициенты модели a. Рекурсия Левинсона-Дурбина является быстрым алгоритмом для решения системы симметричных линейных уравнений Теплица. lpcвесь алгоритм для n = 4 является
r = xcorr(x);
r(1:length(x)-1) = []; % Remove corr. at negative lags
a = levinson(r,4)
Можно сформировать коэффициенты линейного предсказания с другими допущениями, передав другую оценку корреляции в levinson, такой как смещенная оценка корреляции:
r = xcorr(x,'biased'); r(1:length(x)-1) = []; % Remove corr. at negative lags a = levinson(r,4)
prony функция моделирует сигнал с использованием заданного количества полюсов и нулей. Задается последовательность x и порядки числителя и знаменателя n и m, соответственно, оператор
[b,a] = prony(x,n,m)
находит коэффициенты числителя и знаменателя БИХ, импульсная характеристика которого аппроксимирует последовательность x.
prony функция реализует метод, описанный в [4] Parks и Burrus. Этот метод использует изменение ковариационного метода AR-моделирования, чтобы найти коэффициенты знаменателя aи затем находит коэффициенты числителя b для которого импульсная характеристика полученного фильтра точно совпадает с первой n + 1 выборки x. Фильтр не обязательно является стабильным, но он потенциально может восстановить коэффициенты точно, если последовательность данных является действительно авторегрессивным процессом скользящего среднего (ARMA) правильного порядка.
Примечание
Функции prony и stmcb (описаны далее) более точно описаны как модели ARX в терминологии системы идентификации. Моделирование ARMA принимает шум только на входах, в то время как ARX принимает внешний вход. prony и stmcb знать входной сигнал: это импульс для prony и является произвольным для stmcb.
Модель для тестовой последовательности x (из более ранних lpc пример) использование БИХ третьего порядка
[b,a] = prony(x,3,3)
impz команда показывает, насколько хорошо импульсная характеристика этого фильтра соответствует исходной последовательности:
format long
[x impz(b,a,10)]
Заметьте, что первые четыре выборки точно совпадают. Для примера точного восстановления восстановите коэффициенты фильтра Баттерворта из его импульсной характеристики:
[b,a] = butter(4,.2); h = impz(b,a,26); [bb,aa] = prony(h,4,4);
Попробуйте этот пример; вы увидите это bb и aa соответствовать исходным коэффициентам фильтра в пределах допуска 10-13.
stmcb функция определяет коэффициенты для системного b (z )/ a (z), заданные как аппроксимация импульсной характеристики x, а также желаемое количество нулей и полюсов. Эта функция идентифицирует неизвестную систему на основе как входной, так и выход последовательностей, которые описывают поведение системы или просто импульсную характеристику системы. В режиме по умолчанию, stmcb работает, как prony.
[b,a] = stmcb(x,3,3)
stmcb также находит системы, которые совпадают с заданными входной и выходной последовательностями:
y = filter(1,[1 1],x); % Create an output signal.
[b,a] = stmcb(y,x,0,1)
В этом примере, stmcb правильно определяет систему, используемую для создания y от x.
Метод Штейглица-Макбрайда является быстрым итеративным алгоритмом, который решает для коэффициентов числителя и знаменателя одновременно в попытке минимизировать ошибку сигнала между выходом фильтра и заданным выходным сигналом. Этот алгоритм обычно сходится быстро, но может не сходиться, если порядок модели слишком велик. Что касается prony, stmcbрезультирующий фильтр не обязательно является стабильным из-за его точного подхода моделирования.
stmcb обеспечивает управление несколькими важными алгоритмическими параметрами; измените эти параметры, если у вас возникли проблемы с моделированием данных. Чтобы изменить количество итераций от значения по умолчанию пяти и предоставить начальную оценку для коэффициентов знаменателя:
n = 10; % Number of iterations a = lpc(x,3); % Initial estimates for denominator [b,a] = stmcb(x,3,3,n,a);
Функция использует полнополюсную модель, созданную с prony в качестве первоначальной оценки, когда вы не предоставляете одну из своих собственных.
Сравнение функций lpc, prony, и stmcb, вычислите ошибку сигнала в каждом случае:
a1 = lpc(x,3); [b2,a2] = prony(x,3,3); [b3,a3] = stmcb(x,3,3); [x-impz(1,a1,10) x-impz(b2,a2,10) x-impz(b3,a3,10)]
При сравнении возможностей моделирования для заданного порядка БИХ модели, последний результат показывает, что для этого примера, stmcb выступает лучше всех, далее следуют prony, затем lpc. Эта относительная эффективность типична для функций моделирования.
invfreqs и invfreqz функции реализуют обратные операции freqs и freqz; они находят аналоговую или цифровую передаточную функцию заданного порядка, которая соответствует заданной комплексной частотной характеристике. Хотя следующие примеры демонстрируют invfreqz, обсуждение также относится к invfreqs.
Чтобы восстановить исходные коэффициенты фильтра из частотной характеристики простого цифрового фильтра:
[b,a] = butter(4,0.4) % Design Butterworth lowpass [h,w] = freqz(b,a,64); % Compute frequency response [b4,a4] = invfreqz(h,w,4,4) % Model: n = 4, m = 4
Вектор частот w имеет модули измерения в рад/выборке, и частоты не должны быть равномерно разнесены. invfreqz находит фильтр любого порядка для соответствия частотным данным; пример третьего порядка
[b4,a4] = invfreqz(h,w,3,3) % Find third-order IIR
Оба invfreqs и invfreqz проект фильтров с действительными коэффициентами; для точки данных с положительной частотой fфункции соответствуют частотной характеристике в обоих f и -f.
По умолчанию invfreqz использует метод ошибки уравнения, чтобы идентифицировать лучшую модель из данных. Это находит b и a в
![]()
путем создания системы линейных уравнений и решения их с помощью MATLAB®
\ оператор. Здесь A (w (k)) и B (w (k)) являются преобразованиями Фурье полиномов a и b соответственно на частотной w (k), и n является количеством частотных точек (длина h и w). wt (k) взвешивает ошибку относительно ошибки на разных частотах. Синтаксис
invfreqz(h,w,n,m,wt)
включает вектор взвешивания. В этом режиме фильтр, получающийся от invfreqz не гарантировано быть стабильным.
invfreqz предоставляет превосходный алгоритм («output-error»), который решает прямую задачу минимизации взвешенной суммы квадратичной невязки между фактическими точками частотной характеристики и желаемой характеристикой
![]()
Чтобы использовать этот алгоритм, задайте параметр для счета итерации после параметра вектора веса:
wt = ones(size(w)); % Create unit weighting vector [b30,a30] = invfreqz(h,w,3,3,wt,30) % 30 iterations
Полученный фильтр всегда стабильен.
Графически сравните результаты первого и второго алгоритмов с исходным фильтром Баттерворта с FVTool (и выберите величина и Фазовые Отклики):
fvtool(b,a,b4,a4,b30,a30)
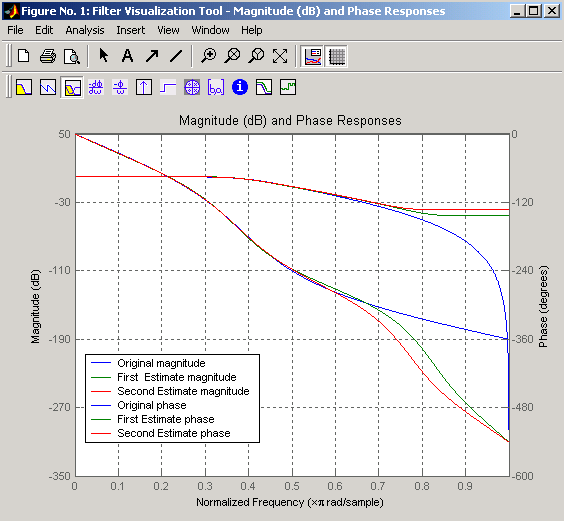
Чтобы проверить превосходство подгонки численно, введите
sum(abs(h-freqz(b4,a4,w)).^2) % Total error, algorithm 1 sum(abs(h-freqz(b30,a30,w)).^2) % Total error, algorithm 2