ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Введение в оДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Вы можете использовать функцию anova1 для выполнения однофакторного дисперсионного анализа (ANOVA). Цель однофакторный дисперсионный анализ состоит в том, чтобы определить, имеют ли данные из нескольких групп (уровней) фактора общее среднее значение. То есть однофакторный дисперсионный анализ позволяет вам выяснить, имеют ли различные группы независимой переменной различные эффекты на y переменной отклика. Предположим, что больница хочет определить, уменьшают ли два новых метода планирования время ожидания пациента больше, чем старый способ планирования встреч. В этом случае независимая переменная является методом планирования, а переменная отклика является временем ожидания пациентов.

Однофакторный дисперсионный анализ является простым частным случаем линейной модели. Однофакторный дисперсионный анализ модели является

$y_{i j} = α_{j} + ε_{i j}$

со следующими допущениями:

y _i j является наблюдением, в котором i представляет число наблюдений, а j представляет другую группу (уровень) переменной y. Все _y i j независимы.
α j представляет населению среднее значение для j-й группы (уровень или лечение).
<reservedrangesplaceholder6> <reservedrangesplaceholder5> <reservedrangesplaceholder4> - случайная ошибка, независимая и обычно распределенная, с нулевым средним и постоянным отклонением, т.е. <reservedrangesplaceholder3> <reservedrangesplaceholder2> <reservedrangesplaceholder1> ~ N (0, σ²).

Эта модель также называется моделью средств. Модель предполагает, что столбцы y - постоянный <reservedrangesplaceholder4> <reservedrangesplaceholder3> плюс <reservedrangesplaceholder2> <reservedrangesplaceholder1> <reservedrangesplaceholder0> компонента ошибки. Дисперсионный Анализ помогает определить, все ли константы одинаковы.

Дисперсионный Анализ проверяет гипотезу о том, что все групповые средства равны ( $H_{0} : α_{1} = α_{2} = ... = α_{k}$ ) против альтернативной гипотезы о том, что по крайней мере одна группа отличается от других ( $H_{1} : α_{i} \neq α_{j}$ для, по крайней мере, одного i и j). anova1(y) проверяет равенство средств столбца для данных в матрице y, где каждый столбец является отдельной группой и имеет одинаковое количество наблюдений (т.е. сбалансированный проект). anova1(y,group) проверяет равенство групповых средств, заданное в group, для данных в векторе или матрице y. В этом случае каждая группа или столбец могут иметь разное количество наблюдений (то есть несбалансированный проект).

Дисперсионный Анализ основан на предположении, что все выборочные населения обычно распределены. Известно, что оно является устойчивым к скромным нарушениям этого предположения. Можно проверить допущение нормальности визуально с помощью графика нормальности (normplot). Кроме того, можно использовать одну из функций Statistics and Machine Learning Toolbox™, которая проверяет нормальность: Критерий Андерсона-Дарлинга (adtest), хи-квадратичный тест качества подгонки (chi2gof), тест Jarque-Bera (jbtest), или тест Лилифорса (lillietest).

Подготовка данных для оДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Можно предоставить выборочные данные в виде вектора или матрицы.

Если выборочные данные указаны в векторе, y, затем необходимо предоставить информацию о группировке с помощью group входная переменная: anova1(y,group).
group должен быть числовым вектором, логическим вектором, категориальным вектором, символьным массивом, строковыми массивами или массивом ячеек из векторов символов с одним именем для каждого элемента y. anova1 функция обрабатывает y значения, соответствующие тому же значению group в составе той же группы. Для примера,

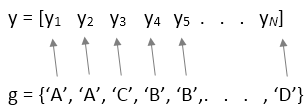
Используйте этот проект, когда группы имеют разное количество элементов (несбалансированное Дисперсионный Анализ).
Если выборочные данные указаны в матрице, y, при условии, что информация о группе опциональна.
- Если вы не задаете переменный вход group, затем anova1 обрабатывает каждый столбец y как отдельная группа и оценивает, равны ли средние значения населения столбцов. Для примера,
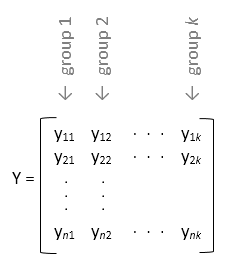
  Используйте эту форму проекта, когда каждая группа имеет одинаковое количество элементов (сбалансированное Дисперсионный Анализ).
- Если вы задаете переменный вход group, затем каждый элемент в group представляет имя группы для соответствующего столбца в y. anova1 функция обрабатывает столбцы с таким же именем группы как часть той же группы. Для примера,

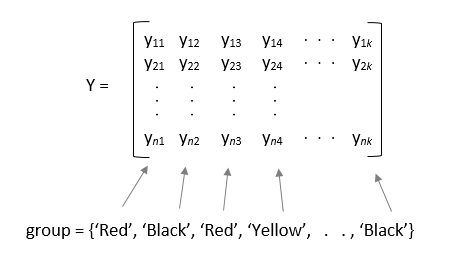
anova1 игнорирует любые NaN значения в y. Кроме того, если group содержит пустые или NaN значения, anova1 игнорирует соответствующие наблюдения в y. anova1 функция выполняет сбалансированный Дисперсионный Анализ, если каждая группа имеет одинаковое количество наблюдений после того, как функция игнорирует пустые или NaN значения. В противном случае, anova1 выполняет несбалансированное Дисперсионный Анализ.

Выполнение оДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Открыть Live Script

В этом примере показано, как выполнить однофакторный дисперсионный анализ, чтобы определить, имеют ли данные из нескольких групп общее среднее значение.

Загрузка и отображение выборочных данных.

load hogg
hogg

hogg = 6×5

    24    14    11     7    19
    15     7     9     7    24
    21    12     7     4    19
    27    17    13     7    15
    33    14    12    12    10
    23    16    18    18    20

Данные получены из исследования Hogg and Ledolter (1987) по количеству бактерий в поставках молока. Столбцы матрицы hogg представляют различные поставки. Строки являются счетчиками бактерий из коробок молока, выбранных случайным образом из каждой партии.

Проверяйте, имеют ли некоторые поставки больше, чем другие. По умолчанию anova1 возвращает два рисунков. Один из них является стандартной таблицей ANOVA, а другой - прямоугольными графиками данных по группам.

[p,tbl,stats] = anova1(hogg);

Figure One-way ANOVA contains objects of type uicontrol.

Figure contains an axes. The axes contains 35 objects of type line.

p = 1.1971e-04

Небольшое значение p около 0,0001 указывает, что количество бактерий от различных поставок не совпадает.

Вы можете получить некоторую графическую уверенность, что средства отличаются, глядя на графики коробки. Выемки, однако, сравнивают медианы, а не средства. Для получения дополнительной информации об этом отображении смотрите boxplot.

Просмотр стандартной таблицы ANOVA. anova1 сохраняет стандартную таблицу ANOVA как массив ячеек в выходном аргументе tbl.

tbl

tbl=4×6 cell array
  Columns 1 through 5

    {'Source' }    {'SS'        }    {'df'}    {'MS'      }    {'F'       }
    {'Columns'}    {[  803.0000]}    {[ 4]}    {[200.7500]}    {[  9.0076]}
    {'Error'  }    {[  557.1667]}    {[25]}    {[ 22.2867]}    {0x0 double}
    {'Total'  }    {[1.3602e+03]}    {[29]}    {0x0 double}    {0x0 double}

  Column 6

    {'Prob>F'    }
    {[1.1971e-04]}
    {0x0 double  }
    {0x0 double  }

Сохраните F-статистическое значение в переменной Fstat.

Fstat = tbl{2,5}

Fstat = 9.0076

Просмотрите статистику, необходимую для многократного парного сравнения средств группы. anova1 сохраняет эту статистику в структуре stats.

stats

stats = struct with fields:
    gnames: [5x1 char]
         n: [6 6 6 6 6]
    source: 'anova1'
     means: [23.8333 13.3333 11.6667 9.1667 17.8333]
        df: 25
         s: 4.7209

Дисперсионный Анализ отвергает нулевую гипотезу о том, что все значения группы равны, поэтому можно использовать несколько сравнений, чтобы определить, какие значения группы отличаются от других. Чтобы провести несколько сравнительных тестов, используйте функцию multcompare, который принимает stats как входной параметр. В этом примере anova1 отклоняет нулевую гипотезу о том, что среднее количество бактерий от всех четырех поставок равно друг другу, т.е., $H_{0} : μ_{1} = μ_{2} = μ_{3} = μ_{4}$ .

Выполните многократный сравнительный тест, чтобы определить, какие поставки отличаются от других с точки зрения среднего количества бактерий.

multcompare(stats)

Figure Multiple comparison of means contains an axes. The axes with title Click on the group you want to test contains 11 objects of type line.

ans = 10×6

    1.0000    2.0000    2.4953   10.5000   18.5047    0.0059
    1.0000    3.0000    4.1619   12.1667   20.1714    0.0013
    1.0000    4.0000    6.6619   14.6667   22.6714    0.0001
    1.0000    5.0000   -2.0047    6.0000   14.0047    0.2119
    2.0000    3.0000   -6.3381    1.6667    9.6714    0.9719
    2.0000    4.0000   -3.8381    4.1667   12.1714    0.5544
    2.0000    5.0000  -12.5047   -4.5000    3.5047    0.4806
    3.0000    4.0000   -5.5047    2.5000   10.5047    0.8876
    3.0000    5.0000  -14.1714   -6.1667    1.8381    0.1905
    4.0000    5.0000  -16.6714   -8.6667   -0.6619    0.0292

Первые два столбца показывают, какие групповые средства сравниваются друг с другом. Для примера в первой строке сравниваются средства для групп 1 и 2. В последнем столбце показаны значения p для тестов. Значения p 0,0059, 0,0013 и 0,0001 показывают, что среднее количество бактерий в молоке от первой партии отличается от среднего количества бактерий от второй, третьей и четвертой партий. Значение p 0,0292 указывает, что среднее количество бактерий в молоке от четвертой партии отличается от среднего количества бактерий от пятого. Процедура не отклоняет гипотезы о том, что другие значения группы отличаются друг от друга.

Рисунок также иллюстрирует тот же результат. Синяя полоса показывает интервал сравнения для среднего значения первой группы, который не перекрывается с интервалами сравнения для второго, третьего и четвертого средств группы, показанными красным цветом. Интервал сравнения для среднего значения пятой группы, показанный серым цветом, перекрывается с интервалом сравнения для среднего значения первой группы. Следовательно, групповые средства для первой и пятой групп незначительно отличаются друг от друга.

Математические детали

Дисперсионный Анализ проверяет различие в группах путем разбиения общего изменения данных на два компонента:

Изменение группы означает от общего среднего, т.е., ${\bar{y}}_{. j} - {\bar{y}}_{..}$ (изменение между группами), где ${\bar{y}}_{. j}$ - выборка для группы j, и ${\bar{y}}_{..}$ - общее среднее значение выборки.
Изменение наблюдений в каждой группе от средних оценок их групп, $y_{i j} - {\bar{y}}_{. j}$ (изменение внутри группы).

Другими словами, Дисперсионный Анализ разбивает общую сумму квадратов (SST) на сумму квадратов из-за эффекта между группами (SSR) и суммы квадратичных невязок (SSE).

$\underset{S S T}{\underset{︸}{\sum_{i} \sum_{j} {(y_{i j} - {\bar{y}}_{..})}^{2}}} = \underset{S S R}{\underset{︸}{\sum_{j} n_{j} {({\bar{y}}_{. j} - {\bar{y}}_{..})}^{2}}} + \underset{S S E}{\underset{︸}{\sum_{i} \sum_{j} {(y_{i j} - {\bar{y}}_{. j})}^{2}}},$

где _nj - размер выборки для j-й группы, j = 1, 2,..., k.

Затем Дисперсионный Анализ сравнивает изменения между группами с изменениями внутри групп. Если отношение изменения между группами к изменению внутри группы значительно велико, можно сделать вывод, что среднее значение группы значительно отличается друг от друга. Можно измерить это с помощью тестовой статистики, которая имеет F -распределение с (k - 1, N - k) степенями свободы:

$F = \frac{\frac{S S R}{k - 1}}{\frac{S S E}{N - k}} = \frac{M S R}{M S E} ~ F_{k - 1, N - k},$

где MSR - средняя квадратная обработка, MSE - средняя квадратичная невязка, k - количество групп, и N - общее количество наблюдений. Если p -value для F -statistic меньше уровня значимости, то тест отвергает нулевую гипотезу о том, что все групповые средства равны, и делает вывод, что, по крайней мере, одно из групповых средств отличается от других. Наиболее распространенными уровнями значимости являются 0,05 и 0,01.

Дисперсионный Анализ

Таблица ANOVA захватывает изменчивость модели по источникам, F-статичную для проверки значимости этой изменчивости и p-значение для принятия решения о значимости этой изменчивости. Значение p, возвращенное anova1 зависит от допущений о случайных возмущениях ε _i j в уравнении модели. Чтобы p-значение было правильным, эти нарушения порядка должны быть независимыми, обычно распределенными и иметь постоянное отклонение. Стандартная таблица ANOVA имеет следующую форму:

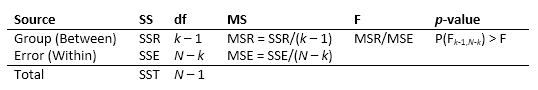
anova1 возвращает стандартную таблицу ANOVA в виде массива ячеек с шестью столбцами.

Столбец	Определение
`Source`	Источник изменчивости.
`SS`	Сумма квадратов по каждому источнику.
`df`	Степени свободы, связанные с каждым источником. Предположим N что это общее количество наблюдений, а k - количество групп. Затем N - k является степенями свободы внутри групп (`Error`), k - 1 является степенями свободы между группами (`Columns`), а N - 1 - суммарные степени свободы: N - 1 = (N - k) + (k - 1).
`MS`	Средние квадраты для каждого источника, что является отношением `SS/df`.
`F`	F -статистический, который является отношением средних квадратов.
`Prob>F`	p -value, которая является вероятностью того, что F-statistic может взять значение, больше вычисленного тестово-статистического значения`. anova1` выводит эту вероятность из cdf F -распределения.

Строки таблицы ANOVA показывают изменчивость данных, разделенных на источник.

Строка (источник)	Определение
`Groups` или `Columns`	Изменчивость из-за различий между группами означает (изменчивость между группами)
`Error`	Изменчивость из-за различий между данными в каждой группе и средним значением группы (изменчивость в группах)
`Total`	Общая изменчивость

Ссылки

[1] Wu, C. F. J., and M. Hamada. Эксперименты: Планирование, анализ и оптимизация проекта параметров, 2000.

[2] Нетер, Дж., М. Х. Кутнер, К. Дж. Нахтсхайм и У. Вассерман. 4-е ред. Прикладные линейные статистические модели. Ирвин Пресс, 1996.

См. также

anova1 | kruskalwallis | multcompare

Документация