Мы узнали, как дискретные вейвлеты преобразования могут использоваться для анализа или разложения сигналов и изображений. Этот процесс называется разложением или анализом. Другая половина истории состоит в том, как эти компоненты могут быть собраны обратно в исходный сигнал без потери информации. Этот процесс называется реконструкцией, или синтезом. Математическая манипуляция, которая влияет на синтез, называется обратным дискретным вейвлет (IDWT).
Чтобы синтезировать сигнал с помощью программного обеспечения Wavelet Toolbox™, мы восстанавливаем его из коэффициентов вейвлета.
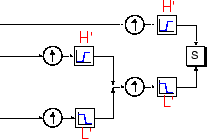
Где вейвлет-анализ включает фильтрацию и понижающую дискретизацию, процесс реконструкции вейвлет состоит из увеличения дискретизации и фильтрации. Усиление дискретизации - это процесс удлинения сигнального компонента путем вставки нулей между выборками.
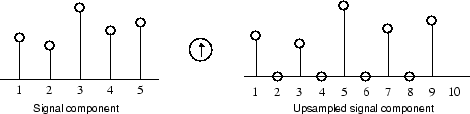
Тулбокс включает команды, такие как idwt и waverec, которые выполняют одноуровневую или многоуровневую реконструкцию, соответственно, компонентов 1-D сигналов. Эти команды имеют свои 2-D и 3-D аналоги, idwt2, waverec2, idwt3, и waverec3.
Фильтрующая часть процесса реконструкции также имеет некоторое обсуждение, потому что именно выбор фильтров имеет решающее значение для достижения идеальной реконструкции исходного сигнала.
Понижающая дискретизация компонентов сигнала, выполненная во время фазы разложения, вносит искажение, называемое сглаживанием. Оказывается, путем тщательного выбора фильтров для фаз разложения и реконструкции, которые тесно связаны (но не идентичны), мы можем «отменить» эффекты сглаживания.
Техническая дискуссия о том, как проектировать эти фильтры, доступна на странице 347 книги Strang and Nguyen Wavelets and Filter Banks. Низко- и высокочастотные фильтры разложения (L и H), вместе со связанными с ними фильтрами реконструкции (L' и H'), образуйте систему так называемых квадратурных зеркальных фильтров:
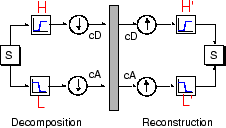
Мы видели, что можно восстановить наш исходный сигнал из коэффициентов приближений и деталей.
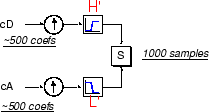
Также возможно восстановить сами приближения и детали из их векторов коэффициентов. В качестве примера давайте рассмотрим, как бы мы восстановили приближение первого уровня A1 от вектора коэффициентов cA1.
Передадим вектор коэффициентов cA1 через тот же процесс мы использовали для восстановления исходного сигнала. Однако вместо объединения с деталями уровня один cD1, мы питаем в нулевом векторе вместо вектора коэффициентов детализации:
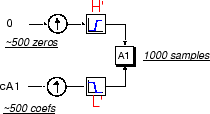
Процесс приводит к восстановленному приближению
A1, которая имеет ту же длину, что и исходный сигнал S и что является его реальным приближением.
Точно так же мы можем восстановить деталь первого уровня D1, используя аналогичный процесс:
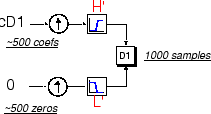
Восстановленные детали и приближения являются истинными составляющими исходного сигнала. На самом деле, мы находим, когда мы объединяем их, что
<reservedrangesplaceholder2> 1 + <reservedrangesplaceholder1> 1 = S.
Обратите внимание, что векторы коэффициентов cA1 и cD1 - потому что они были получены с помощью понижающей дискретизации и составляют только половину длины исходного сигнала - не могут быть непосредственно объединены, чтобы воспроизвести сигнал. Необходимо восстановить приближения и детали перед их объединением.
Распространяя этот метод на компоненты многоуровневого анализа, мы обнаруживаем, что аналогичные отношения сохраняются для всех восстановленных составляющих сигнала. То есть существует несколько способов повторной сборки исходного сигнала:
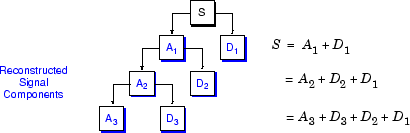
В разделе «Фильтры реконструкции» мы говорили о важности выбора правильных фильтров. На самом деле, выбор фильтров не только определяет, возможно ли совершенное восстановление, но и определяет форму вейвлета, который мы используем для выполнения анализа.
Чтобы создать вейвлет некоторой практической утилиты, вы редко начинаете с рисования формы волны. Вместо этого обычно имеет больше смысла проектировать соответствующие квадратурные зеркальные фильтры, а затем использовать их для создания формы волны. Посмотрим, как это делается, ориентируясь на пример.
Рассмотрим фильтр реконструкции lowpass (L') для db2 вейвлет.
Коэффициенты фильтра могут быть получены из dbaux функция. Изменив порядок вектора масштабирующего фильтра и умножив каждый четный элемент (индексация от 1) на (-1), вы получите фильтр высоких частот.
Многократное увеличение дискретизации на два и свертка выхода с помощью масштабирующего фильтра создает вейвлет экстремальной фазы Daubechies.
L = dbaux(2); H = wrev(L).*[1 -1 1 -1]; HU = dyadup(H,0); HU = conv(HU,L); plot(HU); title('1st Iteration'); H1 = conv(dyadup(HU,0),L); H2 = conv(dyadup(H1,0),L); H3 = conv(dyadup(H2,0),L); H4 = conv(dyadup(H3,0),L); figure; for k =1:4 subplot(2,2,k); eval(['plot(H' num2str(k) ')']); axis tight; end
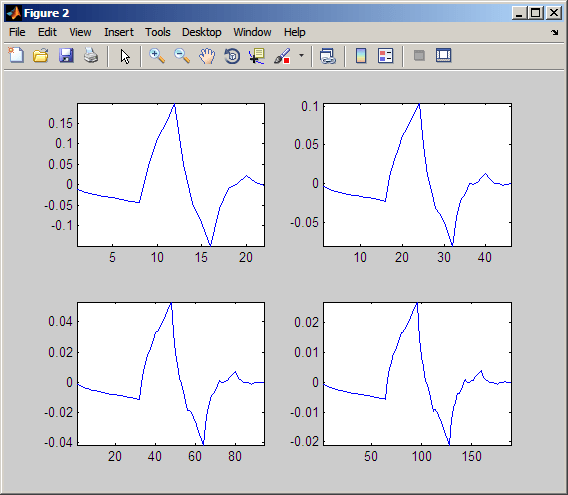
Кривая начинает постепенно больше напоминать db2 вейвлет. Это означает, что форма вейвлета полностью определяется коэффициентами восстановительных фильтров.
Эти отношения имеют глубокие последствия. Это означает, что вы не можете выбрать просто любую форму, назвать ее вейвлет и выполнить анализ. По крайней мере, вы не можете выбрать произвольный вейвлет волны, если хотите иметь возможность точно восстановить исходный сигнал. Вы вынуждены выбрать форму, определенную фильтрами квадратурного зеркального разложения.
Мы видели взаимосвязь вейвлетов и квадратурных зеркальных фильтров. Функция вейвлета и d определяется высокочастотным фильтром, который также производит детали вейвлета разложения.
Существует дополнительная функция, связанная с некоторыми, но не всеми вейвлетами. Это так называемая функция масштабирования, Функция масштабирования очень похожа на функцию вейвлета. Это определяется низкочастотными квадратурными зеркальными фильтрами и, таким образом, связано с приближениями вейвлет.
Таким же образом, что итерационное увеличение дискретизации и свертка фильтра высоких частот создает форму, аппроксимирующую функцию вейвлета, итерационное увеличение дискретизации и свертка фильтра lowpass создает форму, аппроксимирующую функцию масштабирования.