Непрерывное 1-D вейвлет
Эта версия cwt больше не рекомендуется. Использовать обновленный cwt вместо этого.
coefs = cwt(x,scales,'wname')
coefs = cwt(x,scales,'wname','plot')
coefs = cwt(x,scales,'wname','coloration')
coefs = cwt(x,scales,'wname','coloration',xlim)
[coefs,sgram] = cwt(x,scales,'wname','scal')
[coefs,sgram] = cwt(x,scales,'wname','scalCNT')
[coefs,frequencies] = cwt(x,scales,wname,
samplingperiod)
[coefs,sgram,frequencies] = cwt(x,scales,wname,
samplingperiod,'scal')
coefs = cwt(x,scales,' возвращает непрерывное вейвлет (CWT) действительного сигнала wname')x. Вейвлет- преобразование вычисляется для заданных шкал с помощью анализирующего вейвлета wname. scales является вектором 1-D с положительными элементами. Вектор символов или строковый скаляр wname обозначает вейвлет, распознаваемый как wavemngr. coefs - матрица с количеством строк, равным длине scales и количество столбцов, равное длине входного сигнала. K-я строка coefs соответствует коэффициентам CWT для k-й элемент в векторе шкал.
coefs = cwt(x,scales,' строит графики коэффициентов непрерывного вейвлет с помощью wname','plot')coloration по умолчанию
'absglb'.
coefs = cwt(x,scales,' использует указанную окраску. Дополнительные сведения о параметрах окраски см. в разделе «Дополнительные сведения».wname','coloration')
coefs = cwt(x,scales,' окрашивает коэффициенты, используя окрашивание и wname','coloration',xlim)xlim, где xlim является вектором, [x1 x2], с 1 ≤ x1 <x2 ≤ length(x).
[coefs,sgram] = cwt(x,scales,' возвращает и строит график скалограммы. wname','scal')'scal' формирует график изображения скалограммы.
[coefs,sgram] = cwt(x,scales,' отображение представления контура скалограммы. wname','scalCNT')
[coefs,frequencies] = cwt(x,scales, возвращает частоты в циклах в модулях времени, соответствующих шкалам и анализирующему вейвлет wname,
samplingperiod)wname. samplingperiod является положительным реальным скаляром. Если в единицах samplingperiod являются секундами, частоты указаны в герцах.
[coefs,sgram,frequencies] = cwt(x,scales, возвращает скалограмму и частоты, соответствующие шкалам и анализирующему вейвлет. Если у вас есть по крайней мере два элемента в wname,
samplingperiod,'scal')scales, можно также использовать флаг 'scalCNT' для вывода скалограммы. The samplingperiod используется только в преобразовании шкал в частоты. Определение samplingperiod не влияет на внешний вид графиков, сгенерированных cwt.
Постройте график непрерывного преобразования вейвлета и скалограммы с помощью вейвлета sym2 во всех целых числах шкал от 1 до 32, используя фрактальный сигнал как вход:
load vonkoch
vonkoch=vonkoch(1:510);
len = length(vonkoch);
cw1 = cwt(vonkoch,1:32,'sym2','plot');
title('Continuous Transform, absolute coefficients.')
ylabel('Scale')
[cw1,sc] = cwt(vonkoch,1:32,'sym2','scal');
title('Scalogram')
ylabel('Scale')
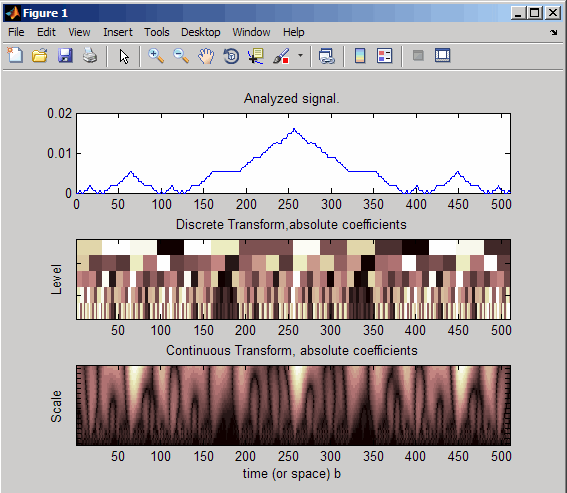
Сравните дискретные и непрерывные вейвлет, используя фрактальный сигнал в качестве входных параметров:
load vonkoch
vonkoch=vonkoch(1:510);
len=length(vonkoch);
[c,l]=wavedec(vonkoch,5,'sym2');
% Compute and reshape DWT to compare with CWT.
cfd=zeros(5,len);
for k=1:5
d=detcoef(c,l,k);
d=d(ones(1,2^k),:);
cfd(k,:)=wkeep(d(:)',len);
end
cfd=cfd(:);
I=find(abs(cfd) <sqrt(eps));
cfd(I)=zeros(size(I));
cfd=reshape(cfd,5,len);
% Plot DWT.
subplot(311); plot(vonkoch); title('Analyzed signal.');
set(gca,'xlim',[0 510]);
subplot(312);
image(flipud(wcodemat(cfd,255,'row')));
colormap(pink(255));
set(gca,'yticklabel',[]);
title('Discrete Transform,absolute coefficients');
ylabel('Level');
% Compute CWT and compare with DWT
subplot(313);
ccfs=cwt(vonkoch,1:32,'sym2','plot');
title('Continuous Transform, absolute coefficients');
set(gca,'yticklabel',[]);
ylabel('Scale');
Daubechies, I. Ten Lectures on Wavelets, Philadelphia, PA: Society for Industrial and Applied Mathematics (SIAM), 1992.
Mallat, S. A Wavelet Tour of Signal Processing, San Diego, CA: Academic Press, 1998.