Глобально выровняйте две последовательности с помощью алгоритма Needleman-Wunsch
Score = nwalign(Seq1,Seq2)
[Score, Alignment] = nwalign(Seq1,Seq2)
[Score, Alignment, Start]
= nwalign(Seq1,Seq2)
... = nwalign(Seq1,Seq2,
...'Alphabet', AlphabetValue, ...)
... = nwalign(Seq1,Seq2,
...'ScoringMatrix', ScoringMatrixValue,
...)
... = nwalign(Seq1,Seq2,
...'Scale', ScaleValue, ...)
... = nwalign(Seq1,Seq2,
...'GapOpen', GapOpenValue, ...)
... = nwalign(Seq1,Seq2,
...'ExtendGap', ExtendGapValue, ...)
... = nwalign(Seq1,Seq2,
...'Glocal', GlocalValue, ...)
... = nwalign(Seq1,Seq2,
...'Showscore', ShowscoreValue, ...)
Seq1, Seq2 | Аминокислота или последовательности нуклеотида. Введите любое следующее: СоветДля справки с буквой и целочисленными представлениями аминокислот и нуклеотидов, смотрите Поиск Поиска или Нуклеотида Аминокислоты. |
AlphabetValue | Вектор символов или строка, задающая тип последовательности. Выбором является 'AA' (значение по умолчанию) или 'NT'. |
ScoringMatrixValue | Любое из следующего:
ПримечаниеЕсли необходимо скомпилировать |
ScaleValue | Положительное значение, которое задает масштабный коэффициент, который применяется к выходному счету. Например, если выходной счет первоначально определяется в битах, и вы вводите Значением по умолчанию является ПримечаниеЕсли свойство СоветПрежде, чем сравнить очки выравнивания от нескольких выравниваний, гарантируйте, что очки находятся в тех же модулях. Можно использовать свойство |
GapOpenValue | Положительное значение, задающее штраф за открытие разрыва в выравнивании. Значением по умолчанию является 8. |
ExtendGapValue | Положительное значение, задающее штраф за расширение разрыва с помощью аффинной схемы штрафа разрыва. ПримечаниеЕсли вы задаете это значение, |
GlocalValue | Управляет возвратом полуглобальной переменной или “glocal” выравниванием. В полуглобальном выравнивании штрафы разрыва в конце последовательностей являются пустыми. Выбором является true или false (значение по умолчанию). |
ShowscoreValue | Управляет отображением пробела выигрыша и путем к победе выравнивания. Выбором является true или false (значение по умолчанию). |
Score | Оптимальное глобальное выравнивание выигрывает в битах. |
Alignment | 3 N символьным массивом, показывающим эти две последовательности, Seq1 и Seq2, в первых и третьих строках и символах, представляющих оптимальное глобальное выравнивание для них во второй строке. |
Start | 2 1 вектор индексов, указывающих на отправную точку в каждой последовательности для выравнивания. Поскольку это - глобальное выравнивание, Start всегда является [1;1]. |
Score = nwalign(Seq1,Seq2)
[ возвращает 3 N символьным массивом, показывающим эти две последовательности, Score, Alignment] = nwalign(Seq1,Seq2)Seq1 и Seq2, в первых и третьих строках и символах, представляющих оптимальное глобальное выравнивание для них во второй строке. Символ | указывает на аминокислоты или нуклеотиды то соответствие точно. : символа указывает на аминокислоты или нуклеотиды, которые связаны, как задано матрицей выигрыша (несовпадения с нулем или положительным выигрывающим матричным значением).
[ возвращается 2 1 вектор индексов, указывающих на отправную точку в каждой последовательности для выравнивания. Поскольку это - глобальное выравнивание, Score, Alignment, Start]
= nwalign(Seq1,Seq2)Start всегда является [1;1].
... = nwalign(Seq1,Seq2, ...'PropertyName', PropertyValue, ...) nwalign с дополнительными свойствами, которые используют имя свойства / пары значения свойства. Можно задать одно или несколько свойств в любом порядке. Каждый PropertyName должен быть заключен в одинарные кавычки и нечувствительный к регистру. Это имя свойства / пары значения свойства следующие:
... = nwalign( задает тип последовательностей. Выбором является Seq1,Seq2,
...'Alphabet', AlphabetValue, ...)'AA' (значение по умолчанию) или 'NT'.
... = nwalign( задает матрицу выигрыша, чтобы использовать для глобального выравнивания. Значение по умолчанию:Seq1,Seq2,
...'ScoringMatrix', ScoringMatrixValue,
...)
'BLOSUM50' — Когда AlphabetValue равняется 'AA'
'NUC44' — Когда AlphabetValue равняется 'NT'
... = nwalign( задает масштабный коэффициент, который применяется к выходному счету, таким образом, управляя модулями выходного счета. Выбором является любое положительное значение.Seq1,Seq2,
...'Scale', ScaleValue, ...)
... = nwalign( задает штраф за открытие разрыва в выравнивании. Выбором является любое положительное значение. Значением по умолчанию является Seq1,Seq2,
...'GapOpen', GapOpenValue, ...)8.
... = nwalign( задает штраф за расширение разрыва с помощью аффинной схемы штрафа разрыва. Выбором является любое положительное значение. Seq1,Seq2,
...'ExtendGap', ExtendGapValue, ...)
... = nwalign( управляет возвратом полуглобальной переменной или “glocal” выравниванием. В полуглобальном выравнивании штрафы разрыва в конце последовательностей являются пустыми. Выбором является Seq1,Seq2,
...'Glocal', GlocalValue, ...)true или false (значение по умолчанию).
... = nwalign( управляет отображением пробела выигрыша и завоевания пути выравнивания. Выбором является Seq1,Seq2,
...'Showscore', ShowscoreValue, ...)true или false (значение по умолчанию).
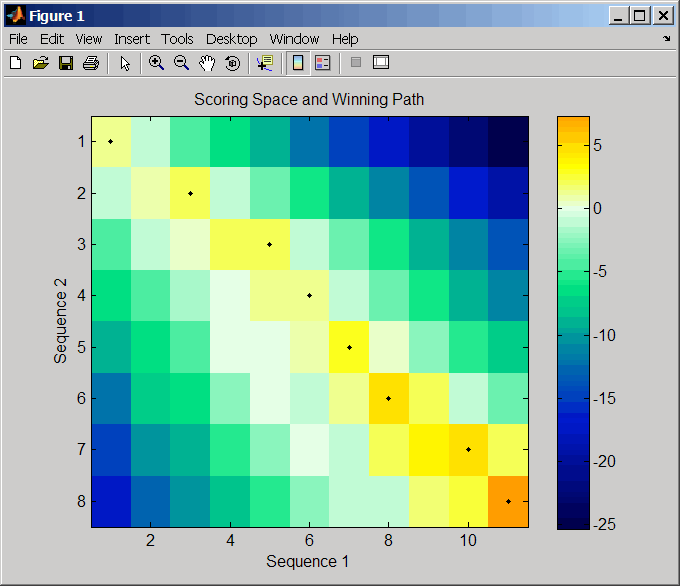
Пробел выигрыша является картой тепла, отображающей лучшую музыку ко всем частичным выравниваниям двух последовательностей. Цвет каждого (n1,n2), координата на пробеле выигрыша представляет лучший счет к соединению подпоследовательностей Seq1(1:n1) и Seq2(1:n2), где n1 является положением в Seq1 и n2, является положением в Seq2. Лучший счет к соединению определенных подпоследовательностей определяется путем выигрыша всех возможных выравниваний подпоследовательностей путем подведения итогов штрафов разрыва и соответствий.
Путь к победе представлен черными точками на пробеле выигрыша, и это иллюстрирует соединение положений в оптимальном глобальном выравнивании. Цвет последней точки (нижний правый угол) пути к победе представляет оптимальный глобальный счет выравнивания к этим двум последовательностям и является Score выходной параметр, возвращенный nwalign.
Пробел выигрыша визуально указывает, существуют ли потенциальные альтернативные пути к победе, который полезен при выравнивании последовательностей с большими разрывами. Визуальные шаблоны на пробеле выигрыша могут также указать на возможную перестановку последовательности.
Глобально выровняйте две последовательности аминокислот с помощью BLOSUM50 (значение по умолчанию), выигрывающее матрицу и значения по умолчанию для свойств GapOpen и ExtendGap. Возвратите оптимальный глобальный счет выравнивания в битах и символьном массиве выравнивания.
[Score, Alignment] = nwalign('VSPAGMASGYD','IPGKASYD') Score = 7.3333 Alignment = VSPAGMASGYD : | | || || I-P-GKAS-YD
Глобально выровняйте две последовательности аминокислот, задающие матрицу выигрыша PAM250 и разрыв открытый штраф 5.
[Score, Alignment] = nwalign('IGRHRYHIGG','SRYIGRG',... 'scoringmatrix','pam250',... 'gapopen',5) Score = 2.3333 Alignment = IGRHRYHIG-G : || || | -S--RY-IGRG
Глобально выровняйте две последовательности аминокислот, возвращающие Score в туземных модулях (nats) путем определения масштабного коэффициента log(2).
[Score, Alignment] = nwalign('HEAGAWGHEE','PAWHEAE','Scale',log(2)) Score = 0.2310 Alignment = HEAGAWGHE-E || || | --P-AW-HEAE
[1] Durbin, R., вихрь, S., Krogh, A. и Мичисон, G. (1998). Биологический анализ последовательности (издательство Кембриджского университета).
aa2int | aminolookup | baselookup | blosum | dayhoff | gonnet | int2aa | int2nt | localalign | multialign | nt2aa | nt2int | nuc44 | pam | profalign | seqdotplot | showalignment | swalign