Дискретные цепи Маркова

Что такое дискретные цепи Маркова?

Рассмотрите стохастический процесс, принимающий значения в state space. Markov process развивается способом, который независим от пути, который приводит к текущему состоянию. Таким образом, текущее состояние содержит всю информацию, необходимую, чтобы предсказать условные вероятности будущих путей. Эта характеристика называется Markov property. Несмотря на то, что процесс Маркова является определенным типом стохастического процесса, он широко используется в моделировании изменений состояния. Специфика процесса Маркова приводит к теории, которая относительно завершена.

Процессы Маркова могут быть ограничены в различных способах, ведя к прогрессивно более кратким математическим формулировкам. Следующие условия являются примерами ограничений.

Пространство состояний может быть ограничено дискретным набором. Эта характеристика показательна из Markov chain. Вероятности перехода свойства Маркова “соединяют” каждое состояние в цепочке к следующему.
Если пространство состояний конечно, цепочкой является finite-state.
Если процесс развивается на шагах дискретного времени, цепочкой является discrete-time.
Если свойство Маркова независимо от времени, цепочкой является homogeneous.

Econometrics Toolbox™ включает объект модели dtmc, представляющий конечное состояние, дискретное время, гомогенная Цепь Маркова. Даже с ограничениями, объект dtmc имеет большую применимость. Это достаточно устойчиво, чтобы служить во многих сценариях моделирования в эконометрике, и математическая теория хорошо подходит для матричной алгебры MATLAB^®.

Цепи Маркова конечного состояния имеют двойную теорию: один в анализе матрицы и один в дискретных графиках. Объектные функции объекта dtmc подсвечивают эту дуальность. Функции позволяют вам двигаться вперед-назад между числовыми и графическими представлениями. Можно работать с инструментами, которые подходят лучше всего для конкретных аспектов расследования. В частности, традиционные методы собственного значения для определения структуры матрицы перехода соединяются с визуализацией для трассировки эволюции цепочки через ее связанный диграф.

Ключевая возможность любой Цепи Маркова является своим ограничивающим поведением. Эта функция особенно важна в эконометрических приложениях, где производительность прогноза модели зависит от того, имеет ли ее стохастический компонент четко определенное распределение, асимптотически. Объектные функции объекта dtmc позволяют вам исследовать переходное и установившееся поведение цепочки и свойств, которые производят уникальный предел. Другие функции вычисляют ограничивающее распределение и оценивают уровни сходимости или mixing times.

Симуляция базового стохастического процесса подходящей Цепи Маркова является основным принципом приложения. Симуляция может принять форму генерации случайной последовательности изменений состояния от начального состояния или от эволюции времени целого распределения состояний. Симуляция позволяет вам определять статистические характеристики цепочки, которая не может быть очевидна из ее спецификации или теории. В эконометрике Цепи Маркова становятся компонентами больших переключающих режим моделей, где они представляют, переключает экономическую обстановку на нижний регистр. Объект dtmc включает функции для симуляции и визуализации эволюции времени Цепей Маркова.

Теория дискретной цепи Маркова

Любое конечное состояние, дискретное время, гомогенная Цепь Маркова может быть представлена, математически, или ее n-by-n матрица перехода P, где n является количеством состояний или его ориентированным графом D. Несмотря на то, что эти два представления эквивалентны — анализ, выполняемый в одной области, приводит к эквивалентным результатам в другом — существуют существенные различия и в концепции аналитических вопросов и в получившихся алгоритмических решениях. Эта дихотомия лучше всего проиллюстрирована путем сравнения разработки теории в [7], например, с разработками в [6] и [9]. Или с помощью MATLAB дихотомия может быть проиллюстрирована путем сравнения алгоритмов на основе объекта graph и его функций с базовой функциональностью в анализе матрицы.

Полный график для процесса конечного состояния имеет ребра и вероятности перехода между каждым узлом i и любым узлом j. Узлы представляют состояния в Цепи Маркова. В D, если матричная запись _Pij 0, то ребро, соединяющее состояния i и j, удалено. Поэтому D показывает только переходы feasible среди состояний. Кроме того, D может включать self-loops, указывающий на ненулевые вероятности _Pii перехода от i состояния назад к себе. Самовероятности перехода известны как inertia состояния или persistence.

В D walk между состояниями i и j являются последовательностью связанных состояний, которая начинается в i и заканчивается в j и имеет длину по крайней мере двух. path является обходом без повторных состояний. circuit является обходом, в котором i = j, но не присутствуют никакие другие повторные состояния.

j состояния является accessible от i состояния, обозначенного $i \to j$ , если существует обход от i до j. Состояния communicate, обозначенный $i \leftrightarrow j$ , если каждый доступен от другого. Коммуникация является отношением эквивалентности на пространстве состояний, деля его в связывающиеся классы. В теории графов состояния, которые связываются, называются strongly connected components. Для процессов Маркова важные свойства отдельных государств совместно используются всеми другими состояниями в связывающемся классе, и так станьте свойствами самого класса. Эти свойства включают:

Recurrence — Свойство того, чтобы быть доступным от всех состояний, которые доступны. Это свойство эквивалентно асимптотической вероятности возврата, равного 1. Каждая цепочка имеет по крайней мере один текущий класс.
Transience — Свойство того, чтобы не быть текущим, то есть, возможность доступа к состояниям, от которых нет никаких, возвращается. Это свойство эквивалентно асимптотической вероятности возврата, равного 0. Класс с быстротечностью не имеет никакого эффекта на асимптотическое поведение.
Periodicity — Свойство циклического повторения среди нескольких подклассов в классе и сохранении некоторой памяти о начальном состоянии. Период состояния является наибольшим общим делителем длин всех схем, содержащих состояние. Состояния или классы с периодом 1 являются апериодическими. Самоциклы на состояниях гарантируют апериодичность и формируют основание для lazy chains.

Важным свойством цепочки в целом является irreducibility. Цепочка неприводима, если цепочка состоит из одного класса передачи. Состояние или свойства класса становятся свойствами целой цепочки, которая упрощает описание и анализ. Обобщением является unichain, который является цепочкой, состоящей из одного текущего класса и любое количество переходных классов. Важные анализы, связанные с asymptotics, могут быть сфокусированы на текущем классе.

График condensed, который формируется путем консолидации состояний каждого класса в один суперузел, упрощает визуальное понимание полной структуры. В этой фигуре одном ориентированном ребре между суперузлами C1 и C2 соответствуют уникальному направлению перехода между классами.

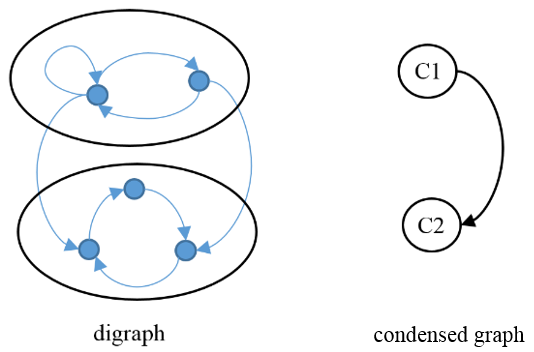
Сжатый график показывает, что C1 является переходным, и C2 является текущим. outdegree C1 положителен, который подразумевает быстротечность. Поскольку C1 содержит самоцикл, это является апериодическим. C2 является периодическим с периодом 3. Одно состояния в с тремя циклами из C2, в более общем периодическом классе, передавая подклассы. Цепочка является приводимым unichain. Вообразите ориентированное ребро от C2 до C1. В этом случае C1 и C2 передают классы, и они выходят из строя в один узел.

Ergodicity, желательное свойство, комбинирует неприводимость с апериодичностью и универсальной формой гарантий ограничение поведения. Поскольку неприводимость является по сути цепочечным свойством, не свойством класса, эргодичность является цепочечным свойством также. Когда используется с unichains, эргодичность означает, что уникальный текущий класс является эргодическим.

С этими определениями возможно обобщить основное существование и теоремы уникальности, связанные с 1 n стационарными дистрибутивами $π^{*}$ , где $π^{*} = π^{*} P$ .

Если P правильный стохастический, то $π^{*} = π^{*} P$ всегда имеет решение для вектора вероятности. Поскольку каждая строка сумм P одной, P имеет правый собственный вектор с собственным значением одного. А именно, e = 1_n, n-by-1 вектор из единиц. Так, P также имеет левый собственный вектор $π^{*}$ с собственным значением одного. В результате Теоремы Крыльца-Frobenius, $π^{*}$ является неотрицательным и может быть нормирован, чтобы произвести вектор вероятности.
$π^{*}$ уникально, если и только если P представляет unichain. В целом, если цепочка содержит k текущие классы, π^* =, π ^*P имеет k линейно независимые решения. В этом случае ^Pm сходится как $m \to \infty$ , но строки не идентичны.
Каждое начальное распределение π ₀ сходится к $π^{*}$ если и только если P представляет эргодический unichain. В этом случае, $π^{*}$ limiting distribution.

Теорема Крыльца-Frobenius является набором результатов, связанных с собственными значениями неотрицательных, неприводимых матриц. Примененный Цепи Маркова, результаты могут быть получены в итоге можно следующим образом. Для конечного состояния unichain, P имеет одно собственное значение λ ₁ = 1 (Perron-Frobenius eigenvalue) с сопроводительным неотрицательным левым собственным вектором $π^{*}$ (который может быть нормирован к вектору вероятности), и правый собственный вектор e = 1_n. Другие собственные значения _λi удовлетворяют $| λ_{i} | \leq 1$ , i = 2, …, n. Если unichain или единственный текущий класс unichain являются апериодическими, то неравенство строго. Когда существует периодичность периода k, существуют собственные значения k на модульном круге в корнях из единицы k. Если unichain является эргодическим, то ^Pm сходится асимптотически к $e π^{*}$ как $m \to \infty$ . Ошибка переходит в 0, по крайней мере, с такой скоростью, как $m^{q} {| λ_{s} |}^{m}$ , где _λs является собственным значением второго по величине значения, и q является кратностью _λs.

Уровень сходимости к $π^{*}$ зависит от second largest eigenvalue modulus (SLEM) $| λ_{SLEM} |$ . Уровень может быть выражен с точки зрения spectral gap, который является $1 - | λ_{SLEM} |$ . Большие разрывы приводят к более быстрой сходимости. mixing time является характеристическим временем для отклонения от равновесия в общем расстоянии изменения. Поскольку сходимость экспоненциальна, смесительное время для затухания фактором e ¹

$T_{соединение} = - \frac{1}{журнал | λ_{SLEM} |} .$

Учитывая теоремы сходимости, смешивая времена должен быть просмотрен в контексте эргодического unichains.

Связанные теоремы в теории неотрицательных, неприводимых матриц дают удобные характеристики двух решающих свойств для равномерной сходимости: приводимость и эргодичность. Предположим, что Z является indicator или zero pattern P, то есть, матрицы с единицами вместо ненулевых записей в P. Затем P неприводим если и только если все записи ${(I + Z)}^{n - 1}$ положительны. Теорема Виландта [11] состояния, что P является эргодическим, если и только если все записи ^Pm положительны для $m > {(n - 1)}^{2} + 1$ .

Теорема Крыльца-Frobenius и связанные результаты неконструктивны для стационарного распределения $π^{*}$ . Существует несколько подходов для вычисления уникального ограничивающего распределения эргодической цепочки.

Задайте _Tii return time, чтобы утвердить, что i является минимальным количеством шагов, чтобы возвратиться, чтобы утвердить i после запуска в i состояния. Кроме того, задайте mean return time _{, τii} является ожидаемым значением _Tii. Затем, $π^{*} = [\begin{matrix} 1 / τ_{11} & \dots & 1 / τ_{n n} \end{matrix}]$ . Этот результат имеет много интуитивного содержимого. Отдельные средние времена смешивания могут быть оценены симуляцией Монте-Карло. Однако издержки симуляции и трудности оценки сходимости, сделайте симуляцию Монте-Карло непрактичной как общий метод.
Поскольку ^Pm приближается к матрице со всеми строками, равными $π^{*}$ как $m \to \infty$ , любая строка “большой мощности” P аппроксимирует π^*. Несмотря на то, что этот метод является прямым, он включает выбор допуска сходимости и соответственно большого m для каждого P. В целом осложнения смешивания временного анализа также делают это вычисление непрактичным.
Линейная система $π^{*} P = π^{*}$ может быть увеличен с ограничением $\sum π^{*} = 1$ , в форме $π^{*} 1_{n - n} = 1_{n}$ , где _1n-by-n является n-by-n матрица из единиц. Используя ограничение, эта система становится

$π^{*} (I - P + 1_{n - n}) = 1_{n} .$
Система может быть решена эффективно с оператором наклонной черты влево MATLAB и численно стабильна, потому что эргодический P не может иметь единиц по основной диагонали (в противном случае, P был бы приводим). Этот метод рекомендуется в [5].
Поскольку $π^{*}$ уникальный левый собственный вектор, сопоставленный с собственным значением Крыльца-Frobenius P, сортирование собственных значений и соответствующих собственных векторов идентифицирует $π^{*}$ . Поскольку ограничение $\sum π^{*} = 1$ не часть задачи о собственных значениях, $π^{*}$ требует нормализации. Этот метод использует устойчивые численные данные функции eigs MATLAB и является подходом, реализованным функцией объекта asymptotics объекта dtmc.

Ссылки

[1] Diebold, F.X., и Г.Д. Рудебуш. Деловые циклы: длительность, динамика и прогнозирование. Принстон, NJ: Издательство Принстонского университета, 1999.

[2] Gallager, R.G. Стохастические процессы: теория для приложений. Кембридж, Великобритания: Издательство Кембриджского университета, 2013.

[3] Gilks, W. R. С. Ричардсон и Д.Дж. Спиджелхэлтер. Цепь Маркова Монте-Карло на практике. Бока-Ратон: Chapman & Hall/CRC, 1996.

[4] Haggstrom, O. Конечные цепи Маркова и алгоритмические приложения. Кембридж, Великобритания: Издательство Кембриджского университета, 2002.

[5] Гамильтон, J. D. Анализ timeseries. Принстон, NJ: Издательство Принстонского университета, 1994.

[6] Рог, R. и К. Р. Джонсон. Анализ матрицы. Кембридж, Великобритания: Издательство Кембриджского университета, 1985.

[7] Джарвис, J. P. и D. R. Более застенчивый. "Теоретический графиком анализ конечных цепей Маркова". В прикладном математическом моделировании: мультидисциплинарный подход. Бока-Ратон: нажатие CRC, 2000.

[8] Maddala, G. S. и я. М. Ким. Модульные корни, коинтеграция и структурное изменение. Кембридж, Великобритания: Издательство Кембриджского университета, 1998.

[9] Монтгомери, J. Математические модели Социальных систем. Неопубликованная рукопись. Отдел Социологии, Висконсинский университет в Мадисоне, 2016.

[10] Норрис, J. R. Цепи Маркова. Кембридж, Великобритания: Издательство Кембриджского университета, 1997.

[11] Wielandt, H. Темы в Аналитической Теории Матриц. Читайте лекции примечаниям, подготовленным Р. Майером. Отдел Математики, Висконсинский университет в Мадисоне, 1967.

Смотрите также

Объекты

dtmc | graph

Функции

asymptotics | classify | eigplot | eigs | graphplot | isergodic | isreducible | lazy | mcmix

Документация