Среда объекта dtmc обеспечивает основные инструменты для моделирования и анализа дискретных цепей Маркова. Цепочки поддержки объектов с конечным числом состояний, которые развиваются в дискретное время с гомогенной временем структурой перехода.
dtmc идентифицирует каждую Цепь Маркова с NumStates-by-NumStates матрица перехода P, независимый от начального состояния x 0 или начальное распределение состояний π 0. Можно задать P или как правильную стохастическую матрицу или как матрицу эмпирических количеств.
Как правильная стохастическая матрица:
Pij является неотрицательной вероятностью перехода от i состояния, чтобы утвердить j.
Каждая строка P суммирует к 1.
описывает эволюцию распределенности со времени t ко времени t + 1.
Распределенность во время t, πt является вектором - строкой из длины NumStates.
Как матрица эмпирических количеств, Pij является наблюдаемым числом раз, утверждают переходы i, чтобы утвердить j. Объект dtmc нормирует строки P так, чтобы это была правильная стохастическая матрица.
Функция mcmix является альтернативным создателем объекта Цепи Маркова; это генерирует цепочку с заданным нулевым шаблоном и случайными вероятностями перехода. mcmix хорошо подходит для создания цепочек с различными временами смешивания для тестирования.
Чтобы визуализировать ориентированного графа или диграф, сопоставленный с цепочкой, используют функцию объекта graphplot. graphplot подобен функции объекта plot
объекта MATLAB® digraph, но это включает дополнительную функциональность для анализа структуры Цепи Маркова. Установки параметров подсвечивают связывающиеся классы (то есть, компоненты strongly connected диграфа) и определенные характеристики, влияющие на сходимость, такие как повторение, быстротечность и периодичность. Можно подсветить вероятности перехода в P путем окраски ребер графика с помощью интенсивности тепловой карты.
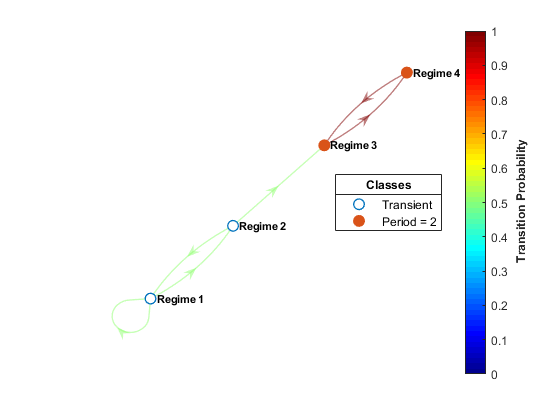
Чтобы визуализировать крупномасштабную структуру в цепочке, graphplot может уплотнить связывающиеся классы к представительным узлам. Эта опция основана на функции объекта condensation объекта digraph.
Функция объекта classify является числовым аналогом выделения класса в графике. classify возвращает характеристики связывающихся классов, которые определяют ограничивающее поведение. Классификация состояния комбинирует теоретические графиком алгоритмы, такие как bfsearch (поиск в ширину) объектная функция объекта MATLAB graph, но с более прямыми матричными вычислениями, характерными для теории Цепи Маркова. Метод subchain позволяет вам извлекать определенные классы передачи от цепочки для последующего анализа.
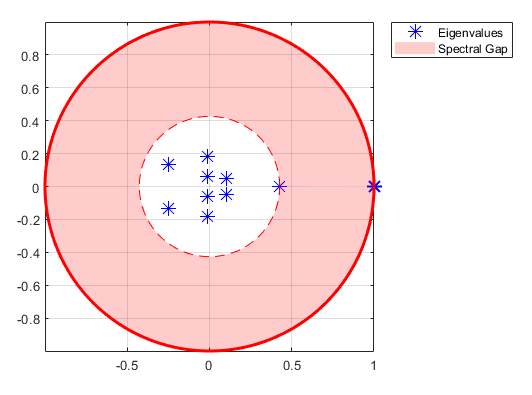
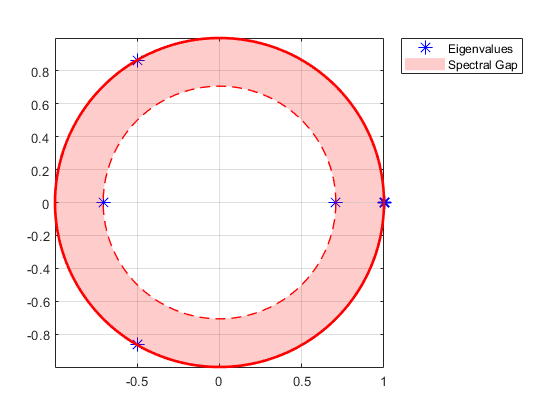
Функции объекта isreducible и isergodic дают краткие сводные данные цепной структуры. Вместе, они обеспечивают необходимые и достаточные условия для существования уникального ограничивающего распределения , где и для каждого начального распределения π 0. Функция объекта asymptotics вычисляет , если это существует и оценивает смесительное время с помощью анализа собственного значения. Графики функций объекта eigplot собственные значения P. Эти данные показывают пример графика собственного значения, возвращенного eigplot.
Одно препятствие сходимости является периодичностью. Функция объекта lazy устраняет периодичность путем корректировки инерции состояния (то есть, путем взвешивания диагональных элементов P), чтобы произвести заданные суммы “лени” в цепочке. Ограничивающие дистрибутивы незатронуты этими преобразованиями.
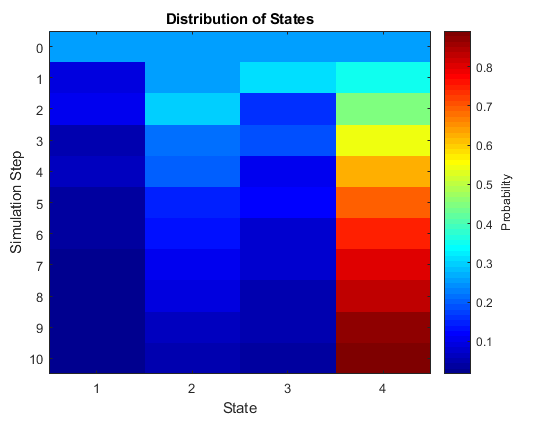
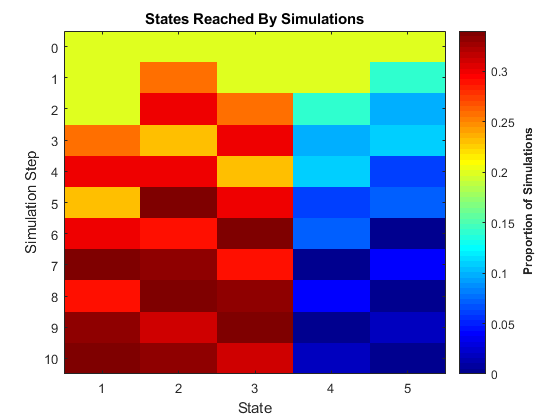
Функции объекта simulate и redistribute обеспечивают реализацию процесса, когда он развивается из заданного начального состояния или распределения. Функции объекта simplot и distplot обеспечивают различную визуализацию. Эта фигура является примером графика распределения, показывающего эволюцию распределенности, начинающей с универсального распределения начального состояния.
Можно начать создавать объект модели Цепи Маркова двумя способами:
Идентифицируйте подходящие дискретные состояния в процессе, и затем оцените вероятности перехода среди них. В самом простом случае теория предлагает цепную структуру и матрицу перехода P. В этой ситуации вы интересуетесь, в основном, тем, как теория теряет значение на практике — что-то, что не всегда очевидно из теории. Если вы знаете P, создаете объект Цепи Маркова путем передачи P dtmc, который реализует теоретическую цепочку.
Если у вас есть менее определенная информация о процессе, то необходимо экспериментировать с различными количествами состояний и выполнимых шаблонов перехода, чтобы воспроизвести эмпирические результаты. Функция mcmix обеспечивает понимание скелетной структуры цепочки, которая может получить существенные особенности в данных. Посредством итеративного процесса можно настроить случайным образом сгенерированную матрицу перехода P, чтобы удовлетворить целям моделирования.
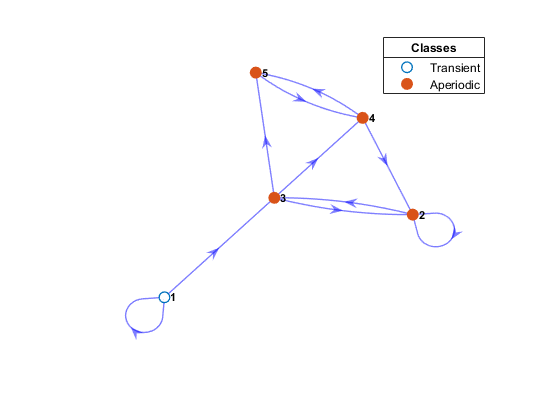
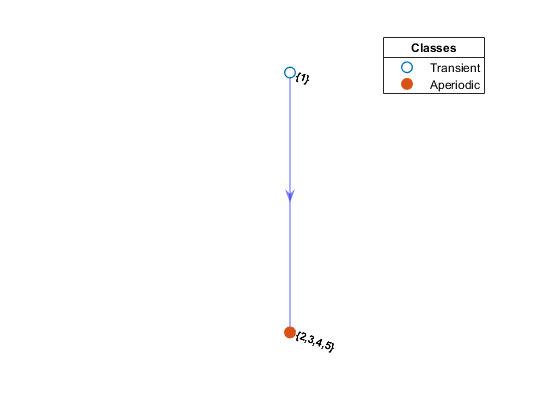
Для разработчика эконометрической модели самым важным последствием выбора P является асимптотическое поведение цепочки. Чтобы понять это поведение, идентифицируйте и разделите переходные состояния (те состояния, чьи возвращаются, разовые вероятности идут, чтобы обнулить асимптотически) от текущих состояний (те состояния, чей возвращаются, разовые вероятности переходят к одной асимптотически). Быстротечность и повторение являются свойствами, совместно использованными всеми состояниями в связывающемся классе. Чтобы определить визуально, являются ли состояния переходными или текущими, передайте объект Цепи Маркова объекту graphplot, функционируют и задают 'ColorNodes',true. Также выходные параметры функции объекта classify обеспечивают числовые инструменты для оценки. Эта фигура является примером диграфа с классифицированными узлами.
Сжатое представление диграфа упрощает эту оценку путем консолидации каждого класса передачи в “суперузел”. В сжатом графике можно легко распознать быстротечность и повторение степень суперузла (степень, больше, чем 0, подразумевает быстротечность). Irreducible chains состоит из одного, обязательно текущего, связывающегося класса. Unichains состоит из одного текущего класса и любого количества спутниковых переходных классов. Unichains поддерживают желательное ограничивающее поведение неприводимой цепочки. Фактор сжатого графика часто является предшественником обрезки цепочки несоответствующих переходных состояний. Функция subchain обрезает цепочки переходных классов. Эта фигура является сжатым представлением диграфа в предыдущей фигуре.
Два принципиальных препятствия универсальному ограничивающему поведению:
Reducibility, существование больше чем одного связывающегося класса
Periodicity, тенденция циклически повториться среди подклассов в едином классе
Комбинация функций объекта graphplot и classify может идентифицировать эти проблемы. Если цепочка приводима и не unichain, распространено разделить анализ среди независимых текущих классов или повторно сформулировать цепочку в целом. Если цепочка является периодической (то есть, она содержит периодический текущий класс), но полная структура получает существенные детали приложения, функция объекта lazy обеспечивает средство. Ленивые цепочки тревожат диагональные элементы P, чтобы устранить периодичность, уезжая asymptotics незатронутый.
Функции объекта isreducible и isergodic обобщают классификацию состояния. Каждая цепочка имеет stationary distribution
, где , в результате P, являющегося стохастическим и имеющего собственное значение одного. Если цепочка неприводима, стационарное распределение уникально. Однако неприводимость, в то время как достаточный, не является необходимым условием для уникальности. Unichains также приводят к уникальному стационарному распределению, имеющему нулевую вероятностную меру в переходных состояниях. В этом отношении анализ классификации состояния важен, потому что isreducible возвращает true, только если цепочка в целом состоит из одного класса передачи. isreducible возвращает false для произвольного unichains, в этом случае необходимо решить, являются ли переходные классы соответствующей частью модели.
Ergodicity или primitivity, является комбинацией неприводимости и апериодичности. Эргодическая цепочка имеет уникальное ограничивающее распределение, то есть, π 0 сходится к для каждого начального распределения π 0. Можно определить, является ли цепочка, в целом, эргодической при помощи isergodic. Функция идентифицирует эргодический unichains путем оценки единственного текущего класса. Цепочка является периодической, если это является неприводимым и не эргодическим, то есть, если ~tfirreduc + ~tfergo = false, куда tfirreduc и tfergo возвращены isreducible и isergodic, соответственно.
Если вы подтвердили, что цепочка является эргодической, можно определить уникальное ограничивающее распределение при помощи функции объекта asymptotics. asymptotics возвращает ограничивающее распределение и оценка смесительного времени, которое является временной константой для затухания переходного поведения. Теорема Крыльца-Frobenius для неприводимых неотрицательных матриц (см. [1]) полезна для интерпретации этих результатов. Любая стохастическая матрица имеет спектральный радиус одного. Периодическим матрицам, периода k, распределили собственные значения k однородно вокруг модульного круга в корнях из единицы k. Значение самого большого собственного значения в модульном кругу определяет уровень затухания переходных состояний. Функция объекта eigplot обеспечивает быструю визуализацию этой информации. Эта фигура является графиком собственного значения Цепи Маркова с периодом три.
Симуляция и перераспределение позволяют вам генерировать статистическую информацию о цепочке, которую трудно вывести непосредственно из теории. Функции объекта simulate и simplot и функции объекта redistribute и distplot, обеспечивают вычислительные и графические инструменты для таких исследований. simulate, например, генерирует независимые случайные обходы через цепочку. Как с функциями объекта simulate в другом месте в Econometrics Toolbox™, средние значения ансамбля зависимой статистики играют важную роль в прогнозировании. Соответствующая функция объекта simplot предлагает несколько подходов к визуализации. Эта фигура отображает пропорцию состояний, которые посещают после 100 случайных обходов длины 10 шагов через периодическую Цепь Маркова в предыдущей фигуре.
[1] Рог, R. и К. Р. Джонсон. Анализ матрицы. Кембридж, Великобритания: Издательство Кембриджского университета, 1985.
bfsearch | condensation | graphplot | mcmix