Задайте модели EGARCH

Модель EGARCH по умолчанию

EGARCH по умолчанию (P, Q) модель в Econometrics Toolbox™ имеет форму

$ε_{t} = σ_{t} z_{t},$

с Гауссовым инновационным распределением и

$журнал σ_{t}^{2} = κ + \sum_{i = 1}^{P} γ_{i} журнал σ_{t - i}^{2} + \sum_{j = 1}^{Q} α_{j} [\frac{| ε_{t - j} |}{σ_{t - j}} - E {\frac{| ε_{t - j} |}{σ_{t - j}}}] + \sum_{j = 1}^{Q} ξ_{j} (\frac{ε_{t - j}}{σ_{t - j}}) .$

Модель по умолчанию имеет значительное смещение, и изолированные логарифмические отклонения и стандартизированные инновации в последовательных задержках.

Можно задать модель этой формы с помощью краткого синтаксиса egarch(P,Q). Для входных параметров P и Q, введите номер изолированных логарифмических отклонений (условия GARCH), P, и изолировал стандартизированные инновации (ДУГА и условия рычагов), Q, соответственно. Следующие ограничения применяются:

P и Q должны быть неотрицательными целыми числами.
Если P> 0, то необходимо также задать Q> 0.

Когда вы используете этот краткий синтаксис, egarch создает модель egarch с этими значениями свойств по умолчанию.

Свойство	Значение по умолчанию
`P`	Количество условий GARCH, P
`Q`	Количество ДУГИ и условий рычагов, Q
`Offset`	0
`Constant`	`NaN`
`GARCH`	Вектор ячейки `NaN` s
`ARCH`	Вектор ячейки `NaN` s
`Leverage`	Вектор ячейки `NaN` s
`Distribution`	`"Gaussian"`

Чтобы присвоить значения не по умолчанию любым свойствам, можно изменить созданную модель с помощью записи через точку.

Чтобы проиллюстрировать, рассмотрите определение модели EGARCH(1,1)

$ε_{t} = σ_{t} z_{t},$

с Гауссовым инновационным распределением и

$журнал σ_{t}^{2} = κ + γ_{1} журнал σ_{t - 1}^{2} + α_{1} [\frac{| ε_{t - 1} |}{σ_{t - 1}} - E {\frac{| ε_{t - 1} |}{σ_{t - 1}}}] + ξ_{1} (\frac{ε_{t - 1}}{σ_{t - 1}}) .$

Mdl = egarch(1,1)

Mdl = 
  egarch with properties:

     Description: "EGARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: 0

Созданная модель, Mdl, имеет NaN s для всех параметров модели. Значение NaN сигнализирует, что параметр должен быть оценен или в противном случае задан пользователем. Все параметры должны быть заданы, чтобы предсказать или моделировать модель

Чтобы оценить параметры, введите модель (наряду с данными) к estimate. Это возвращает новую подходящую модель egarch. Подобранная модель имеет оценки параметра для каждого значения входа NaN.

Вызов egarch без любых входных параметров возвращает спецификацию модели EGARCH(0,0) со значениями свойств по умолчанию:

DefaultMdl = egarch

DefaultMdl = 
  egarch with properties:

     Description: "EGARCH(0,0) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 0
               Q: 0
        Constant: NaN
           GARCH: {}
            ARCH: {}
        Leverage: {}
          Offset: 0

Задайте модель EGARCH по умолчанию

Скрипт Open Live Script

Этот пример показывает, как использовать краткий синтаксис egarch(P,Q), чтобы задать EGARCH по умолчанию (P, Q) модель, $ε_{t} = σ_{t} z_{t}$ с Гауссовым инновационным распределением и

По умолчанию все параметры в созданной модели имеют неизвестные значения.

Задайте модель EGARCH(1,1) по умолчанию:

Mdl = egarch(1,1)

Mdl = 
  egarch with properties:

     Description: "EGARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: 0

Вывод показывает, что созданная модель, Mdl, имеет значения NaN для всех параметров модели: постоянный термин, коэффициент GARCH, коэффициент ДУГИ и коэффициент рычагов. Можно изменить созданную модель с помощью записи через точку или ввести его (наряду с данными) к estimate.

Используя Аргументы в виде пар имя-значение

Самый гибкий способ задать модели EGARCH использует аргументы пары "имя-значение". Вам не нужно, и при этом вы не в состоянии, чтобы задать значение для каждого образцового свойства. egarch присваивает значения по умолчанию любым образцовым свойствам, которые вы не делаете (или не может) задавать.

Общий EGARCH (P, Q) модель имеет форму

$y_{t} = μ + ε_{t},$

где $ε_{t} = σ_{t} z_{t}$ и

Инновационным распределением может быть t Гауссова или Студента. Распределение по умолчанию является Гауссовым.

В порядке оценить, предскажите или моделируйте модель, необходимо задать параметрическую форму модели (например, какие задержки соответствуют ненулевым коэффициентам, инновационному распределению), и любые известные значения параметров. Можно установить любые неизвестные параметры, равные NaN, и затем вводить модель к estimate (наряду с данными), чтобы получить оцененные значения параметров.

egarch (и estimate) возвращает модель, соответствующую образцовой спецификации. Можно изменить модели, чтобы изменить или обновить спецификацию. Введите модели (без значений NaN) к forecast или simulate для прогнозирования и симуляции, соответственно. Вот некоторые спецификации в качестве примера с помощью аргументов значения имени.

Модель	Спецификация
$y_{t} = ε_{t}$ $ε_{t} = σ_{t} z_{t}$ Гауссов _zt $\begin{array}{l} журнал σ_{t}^{2} = κ + γ_{1} журнал σ_{t - 1}^{2} + \dots \\ α_{1} [\frac{\| ε_{t - 1} \|}{σ_{t - 1}} - E {\frac{\| ε_{t - 1} \|}{σ_{t - 1}}}] + ξ_{1} (\frac{ε_{t - 1}}{σ_{t - 1}}) \end{array}$	`egarch ('GARCH', NaN, 'ДУГА', NaN... 'Рычаги', NaN)` или `egarch(1,1)`
$y_{t} = μ + ε_{t}$ $ε_{t} = σ_{t} z_{t}$ Студент _zt t с неизвестными степенями свободы $\begin{array}{l} журнал σ_{t}^{2} = κ + γ_{1} журнал σ_{t - 1}^{2} + \dots \\ α_{1} [\frac{\| ε_{t - 1} \|}{σ_{t - 1}} - E {\frac{\| ε_{t - 1} \|}{σ_{t - 1}}}] + ξ_{1} (\frac{ε_{t - 1}}{σ_{t - 1}}) \end{array}$	`egarch ('Смещение', NaN, 'GARCH', NaN... 'ДУГА', NaN, 'Рычаги', NaN... 'Распределение', 't')`
$y_{t} = ε_{t}$ $ε_{t} = σ_{t} z_{t}$ Студент _zt t с восемью степенями свободы $\begin{array}{l} журнал σ_{t}^{2} = - 0.1 + 0.4 журнал σ_{t - 1}^{2} + \dots \\ 0.3 [\frac{\| ε_{t - 1} \|}{σ_{t - 1}} - E {\frac{\| ε_{t - 1} \|}{σ_{t - 1}}}] - 0.1 (\frac{ε_{t - 1}}{σ_{t - 1}}) \end{array}$	`egarch ('Констант',-0.1, 'GARCH', 0.4... 'ДУГА', 0.3, 'Рычаги',-0.1... 'Распределение', struct ('Имя', 't', 'степень свободы', 8))`

Вот полное описание аргументов значения имени, которые можно использовать, чтобы задать модели EGARCH.

Примечание

Вы не можете присвоить значения свойствам P и Q. egarch устанавливает P, равный самой большой задержке GARCH и Q, равному самой большой задержке с ненулевым стандартизированным инновационным коэффициентом, включая коэффициенты рычагов и ДУГУ.

Аргументы значения имени для моделей EGARCH

Имя	Соответствующий образцовый термин (термины) EGARCH	Когда задать
`Offset`	Среднее смещение, μ	Включать ненулевое среднее смещение. Например, `'Offset',0.2`. Если вы планируете оценить срок смещения, задайте `'Offset',NaN`. По умолчанию `Offset` имеет значение `0` (значение, никакое смещение).
`Constant`	Постоянный в условной модели отклонения, κ	Установить ограничения равенства для κ. Например, если модель знала постоянные –0.1, задайте `'Constant',-0.1`. По умолчанию `Constant` имеет значение `NaN`.
`GARCH`	Коэффициенты GARCH, $γ_{1}, \dots, γ_{P}$	Установить ограничения равенства для коэффициентов GARCH. Например, чтобы задать модель EGARCH(1,1) с $γ_{1} = 0.6,$ задайте `'GARCH',0.6`. Только необходимо указать ненулевые элементы `GARCH`. Если ненулевые коэффициенты в непоследовательных задержках, задают соответствующие задержки с помощью `GARCHLags`. Любые коэффициенты, которые вы задаете, должны удовлетворить все ограничения стационарности.
`GARCHLags`	Задержки, соответствующие ненулевым коэффициентам GARCH	`GARCHLags` не является образцовым свойством. Используйте этот аргумент в качестве ярлыка для определения `GARCH`, когда ненулевые коэффициенты GARCH будут соответствовать непоследовательным задержкам. Например, чтобы задать ненулевые коэффициенты GARCH в задержках 1 и 3, например, ненулевой $γ_{1}$ и $γ_{3},$ задайте `'GARCHLags',[1,3]`. Используйте `GARCH` и `GARCHLags` вместе, чтобы задать известные ненулевые коэффициенты GARCH в непоследовательных задержках. Например, если $γ_{1} = 0.3$ и $γ_{3} = 0.1,$ задайте `'GARCH',{0.3,0.1},'GARCHLags',[1,3]`
`ARCH`	Коэффициенты ДУГИ, $α_{1}, \dots, α_{Q}$	Установить ограничения равенства для коэффициентов ДУГИ. Например, чтобы задать модель EGARCH(1,1) с $α_{1} = 0.3,$ задайте `'ARCH',0.3`. Только необходимо указать ненулевые элементы `ARCH`. Если ненулевые коэффициенты в непоследовательных задержках, задают соответствующие задержки с помощью `ARCHLags`.
`ARCHLags`	Задержки, соответствующие ненулевым коэффициентам ДУГИ	`ARCHLags` не является образцовым свойством. Используйте этот аргумент в качестве ярлыка для определения `ARCH`, когда ненулевые коэффициенты ДУГИ будут соответствовать непоследовательным задержкам. Например, чтобы задать ненулевые коэффициенты ДУГИ в задержках 1 и 3, например, ненулевой $α_{1}$ и $α_{3},$ задайте `'ARCHLags',[1,3]`. Используйте `ARCH` и `ARCHLags` вместе, чтобы задать известные ненулевые коэффициенты ДУГИ в непоследовательных задержках. Например, если $α_{1} = 0.4$ и $α_{3} = 0.2,$ задайте `'ARCH',{0.4,0.2},'ARCHLags',[1,3]`
`Leverage`	Усильте коэффициенты, $ξ_{1}, \dots, ξ_{Q}$	Установить ограничения равенства для коэффициентов рычагов. Например, чтобы задать модель EGARCH(1,1) с $ξ_{1} = - 0.1,$ задайте `'Leverage',-0.1`. Только необходимо указать ненулевые элементы `Leverage`. Если ненулевые коэффициенты в непоследовательных задержках, задают соответствующие задержки с помощью `LeverageLags`.
`LeverageLags`	Задержки, соответствующие ненулевым коэффициентам рычагов	`LeverageLags` не является образцовым свойством. Используйте этот аргумент в качестве ярлыка для определения `Leverage`, когда ненулевые коэффициенты рычагов будут соответствовать непоследовательным задержкам. Например, чтобы задать ненулевые коэффициенты рычагов в задержках 1 и 3, например, ненулевой $ξ_{1}$ и $ξ_{3},$ задайте `'LeverageLags',[1,3]`. Используйте `Leverage` и `LeverageLags` вместе, чтобы задать известные ненулевые коэффициенты рычагов в непоследовательных задержках. Например, если $ξ_{1} = - 0.2$ и $ξ_{3} = - 0.1,$ задайте `'Leverage',{-0.2,-0.1},'LeverageLags',[1,3]`.
`Distribution`	Распределение инновационного процесса	Используйте этот аргумент, чтобы задать инновационное распределение t Студента. По умолчанию инновационное распределение является Гауссовым. Например, чтобы задать распределение t с неизвестными степенями свободы, задайте `'Distribution','t'`. Чтобы задать инновационное распределение t с известными степенями свободы, присвойте `Distribution` структура данных с полями `Name` и `DoF`. Например, для распределения t с девятью степенями свободы, задайте `'Distribution',struct('Name','t','DoF',9)`.

Задайте модель EGARCH Используя приложение Econometric Modeler

Можно задать структуру задержки, инновационное распределение и рычаги моделей EGARCH с помощью приложения Econometric Modeler. Приложение обрабатывает все коэффициенты как неизвестные и допускающие оценку, включая параметр степеней свободы для инновационного распределения t.

В командной строке откройте приложение Econometric Modeler.

econometricModeler

Также откройте приложение из галереи приложений (см. Econometric Modeler).

В приложении вы видите все поддерживаемые модели путем выбора переменной временных рядов для ответа в Data Browser. Затем на вкладке Econometric Modeler, в разделе Models, кликают по стрелке, чтобы отобразить галерею моделей.

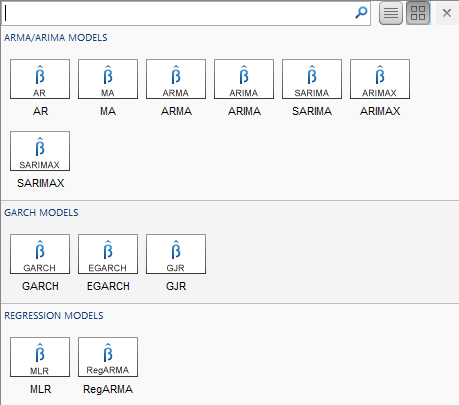
Раздел GARCH Models содержит все поддерживаемые условные модели отклонения. Чтобы задать модель EGARCH, нажмите EGARCH. Диалоговое окно EGARCH Model Parameters появляется.

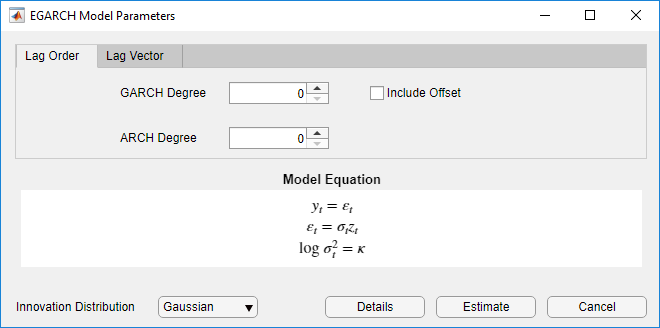
Корректируемые параметры включают:

GARCH Degree – Порядок полинома GARCH.
ARCH Degree – Порядок полинома ДУГИ. Значение этого параметра также задает порядок полинома рычагов.
Include Offset – Включение образцового смещения.
Innovation Distribution – Инновационное распределение.

Когда вы настраиваете значения параметров, уравнение в разделе Model Equation изменяется, чтобы совпадать с вашими спецификациями. Корректируемые параметры соответствуют входному и аргументам пары "имя-значение", описанным в предыдущих разделах и на странице с описанием egarch.

Для получения дополнительной информации при определении моделей с помощью приложения, см. Подходящие Модели к Данным и Задающий Полиномы Оператора Задержки В интерактивном режиме.

Задайте модель EGARCH со средним смещением

Скрипт Open Live Script

Этот пример показывает, как задать EGARCH (P, Q) модель со средним смещением. Используйте аргументы пары "имя-значение", чтобы задать модель, которая отличается от модели по умолчанию.

Задайте модель EGARCH(1,1) со средним смещением,

$y_{t} = μ + ε_{t},$

где $ε_{t} = σ_{t} z_{t}$ и

$журнал σ_{t}^{2} = κ + γ_{1} журнал σ_{t - 1}^{2} + α_{1} [\frac{| ε_{t - 1} |}{σ_{t - 1}} - E {\frac{| ε_{t - 1} |}{σ_{t - 1}}}] + ξ_{1} (\frac{ε_{t - 1}}{σ_{t - 1}}) .$

Mdl = egarch('Offset',NaN,'GARCHLags',1,'ARCHLags',1,...
    'LeverageLags',1)

Mdl = 
  egarch with properties:

     Description: "EGARCH(1,1) Conditional Variance Model with Offset (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: NaN

Среднее смещение, кажется, в выводе как дополнительный параметр оценено или в противном случае задано.

Задайте модель EGARCH с непоследовательными задержками

Скрипт Open Live Script

Этот пример показывает, как задать модель EGARCH с ненулевыми коэффициентами в непоследовательных задержках.

Задайте модель EGARCH(3,1) с ненулевыми условиями GARCH в задержках 1 и 3. Включайте среднее смещение.

Mdl = egarch('Offset',NaN,'GARCHLags',[1,3],'ARCHLags',1,...
    'LeverageLags',1)

Mdl = 
  egarch with properties:

     Description: "EGARCH(3,1) Conditional Variance Model with Offset (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 3
               Q: 1
        Constant: NaN
           GARCH: {NaN NaN} at lags [1 3]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: NaN

Неизвестные ненулевые коэффициенты GARCH соответствуют изолированным логарифмическим отклонениям в задержках 1 и 3. Вывод показывает только ненулевые коэффициенты.

Отобразите значение GARCH:

Mdl.GARCH

ans = 1x3 cell array
    {[NaN]}    {[0]}    {[NaN]}

Массив ячеек GARCH возвращает три элемента. Первые и третьи элементы имеют значение NaN, указывая, что эти коэффициенты являются ненулевыми и должны быть оценены или в противном случае заданы. По умолчанию egarch устанавливает временный коэффициент в задержке 2 равных нулю поддерживать непротиворечивость с индексацией массива ячеек MATLAB®.

Задайте модель EGARCH с известными значениями параметров

Скрипт Open Live Script

Этот пример показывает, как задать модель EGARCH с известными значениями параметров. Можно использовать такую полностью заданную модель в качестве входа к simulate или forecast.

Задайте модель EGARCH(1,1)

$журнал σ_{t}^{2} = 0.1 + 0.6 журнал σ_{t - 1}^{2} + 0.2 [\frac{| ε_{t - 1} |}{σ_{t - 1}} - E {\frac{| ε_{t - 1} |}{σ_{t - 1}}}] - 0.1 (\frac{ε_{t - 1}}{σ_{t - 1}})$

с Гауссовым инновационным распределением.

Mdl = egarch('Constant',0.1,'GARCH',0.6,'ARCH',0.2,...
    'Leverage',-0.1)

Mdl = 
  egarch with properties:

     Description: "EGARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 1
               Q: 1
        Constant: 0.1
           GARCH: {0.6} at lag [1]
            ARCH: {0.2} at lag [1]
        Leverage: {-0.1} at lag [1]
          Offset: 0

Поскольку все значения параметров заданы, созданная модель не имеет никаких значений NaN. Функции simulate и forecast не принимают входные модели со значениями NaN.

Задайте Модель EGARCH с t Инновационным Распределением

Скрипт Open Live Script

Этот пример показывает, как задать модель EGARCH с t инновационным распределением Студента.

Задайте модель EGARCH(1,1) со средним смещением,

$y_{t} = μ + ε_{t},$

где $ε_{t} = σ_{t} z_{t}$ и

$журнал σ_{t}^{2} = κ + γ_{1} журнал σ_{t - 1}^{2} + α_{1} [\frac{| ε_{t - 1} |}{σ_{t - 1}} - E {\frac{| ε_{t - 1} |}{σ_{t - 1}}}] + ξ_{1} (\frac{ε_{t - 1}}{σ_{t - 1}}) .$

Принять $z_{t}$ следует за t инновационным распределением Студента с 10 степенями свободы.

tDist = struct('Name','t','DoF',10);
Mdl = egarch('Offset',NaN,'GARCHLags',1,'ARCHLags',1,...
    'LeverageLags',1,'Distribution',tDist)

Mdl = 
  egarch with properties:

     Description: "EGARCH(1,1) Conditional Variance Model with Offset (t Distribution)"
    Distribution: Name = "t", DoF = 10
               P: 1
               Q: 1
        Constant: NaN
           GARCH: {NaN} at lag [1]
            ARCH: {NaN} at lag [1]
        Leverage: {NaN} at lag [1]
          Offset: NaN

Значение Distribution является массивом struct с полем Name, равным 't' и полю DoF, равному 10. Когда вы задаете степени свободы, они не оцениваются, если вы вводите модель к estimate.

Документация