СТРАНИЦА THIS УСТАРЕВШИЙ РАБОЧИЙ ПРОЦЕСС АЛЬТЕРНАТИВЫ DESCRIBES AN APPLICABLE ONLY FOR 2D ПРОБЛЕМЫ. Для рекомендуемого рабочего процесса смотрите, Решают проблемы Используя Объекты PDEModel. Рабочий процесс, описанный на этой странице, является альтернативой устаревшему рабочему процессу, описанному в, Решают проблемы Используя Устаревшие Объекты PDEModel.
Несмотря на то, что приложение PDE Modeler обеспечивает удобную рабочую среду, существуют ситуации, где гибкость использования функций командной строки необходима. Они включают:
3-D геометрия
Геометрические формы кроме прямых линий, круговых дуг и эллиптических дуг
Нестандартные граничные условия
Сложный УЧП или коэффициенты граничного условия
Больше чем две зависимые переменные в системном случае
Нелокальные ограничения решения
Специальная обработка данных решения и представление перечисляют
Приложение PDE Modeler может все еще быть ценной помощью в некоторых ситуациях, представленных ранее, если часть моделирования сделана с помощью приложения PDE Modeler и затем сделана доступный для использования командной строки через обширные средства экспорта данных приложения PDE Modeler.
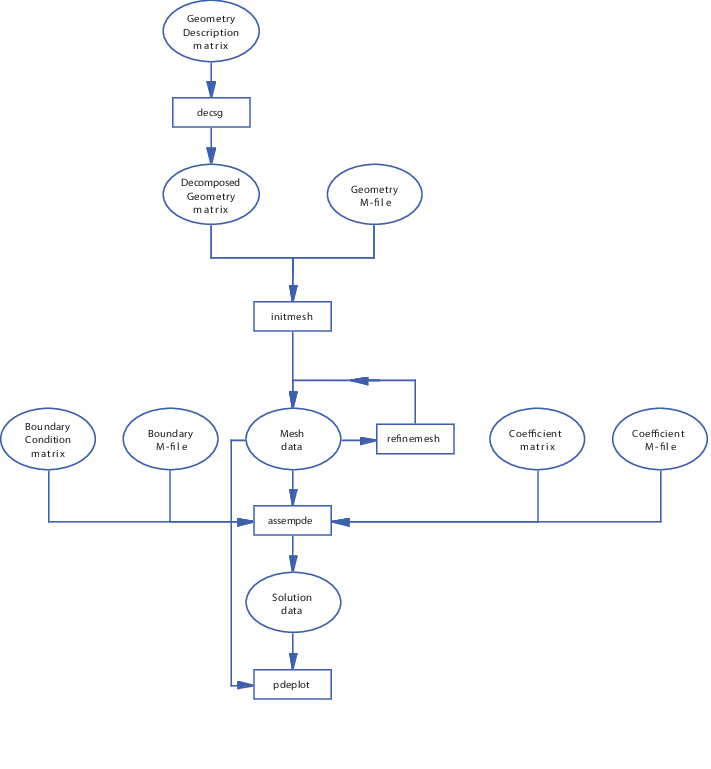
Процесс определения вашей проблемы и решения его отражается в проекте приложения PDE Modeler. Много структур данных задают различные аспекты проблемы, и различные этапы обработки производят новые структуры данных из старых единиц. Смотрите следующую фигуру.
Прямоугольники являются функциями, и замещающие знаки являются данными, представленными матрицами или файлами. Стрелки указывают на данные, необходимые для функций.
Как существует определенное направление в этой схеме, можно сократить в него путем представления необходимых наборов данных, и затем продолжить вниз. В следующих разделах мы даем подсказки к описаниям точных форматов различных структур данных и файлов.
Модель Constructive Solid Geometry (CSG) задана матрицей Описания Геометрии, формулой набора и матрицей Пространства имен. Для описания этих структур данных смотрите страницу с описанием для decsg. На этом уровне проблемная геометрия задана перекрывающимися твердыми объектами. Они могут быть созданы путем рисования модели CSG в приложении PDE Modeler и затем экспортирования данных с помощью опции Export Geometry Description, Set Formula, Labels из меню Draw.
Анализируемая геометрия задана или Анализируемой матрицей Геометрии, или файлом Геометрии. Здесь, геометрия описана как набор непересекающихся минимальных областей, ограниченных граничными сегментами и сегментами границы. Анализируемая матрица Геометрии может быть создана из модели CSG при помощи функционального decsg. Это может также быть экспортировано из приложения PDE Modeler путем выбора опции Export Decomposed Geometry, Boundary Cond's из меню Boundary. Файл Геометрии, эквивалентный данной Анализируемой матрице Геометрии, может быть создан с помощью функции wgeom. Анализируемая геометрия может визуализироваться с функцией pdegplot. Для описаний структур данных Анализируемой матрицы Геометрии и файла Геометрии, смотрите страницу с описанием для decsg и Геометрии.
Они заданы или
матрицей Граничного условия или Массивом данных граничных условий. Граничные условия даны как функции на граничных сегментах. Матрица Граничного условия может быть экспортирована из приложения PDE Modeler путем выбора опции Export Decomposed Geometry, Boundary Cond's из меню Boundary. Для описания структур данных матрицы Граничного условия и Массива данных граничных условий, смотрите страницы с описанием для assemb и смотрите Граничные условия.
УЧП задан или Матрицей коэффициентов или Содействующим файлом для каждого из коэффициентов УЧП c, a, f и d. Коэффициенты являются функциями на субдоменах. Коэффициенты могут быть экспортированы из приложения PDE Modeler путем выбора опции Export PDE Coefficient из меню PDE. Для получения дополнительной информации о содействующих структурах данных уравнения смотрите страницу с описанием для assempde и смотрите Коэффициенты УЧП.
Треугольная mesh описана данными о mesh, которые состоят из матрицы Точки, матрицы Ребра и Треугольной матрицы. В mesh минимальные области триангулированы в субдомены, и сегменты границы и граничные сегменты разбиты в ребра. Сцепитесь данные создаются из анализируемой геометрии функциональным initmesh и могут быть изменены функциями refinemesh и jigglemesh. Опция Export Mesh из меню Mesh обеспечивает другой способ создать данные о mesh. Функция adaptmesh создает данные о mesh как часть процесса решения. Mesh может быть построена с функцией pdemesh. Для получения дополнительной информации на представлении данных mesh, смотрите страницу с описанием для initmesh и смотрите Данные о Mesh.
Решение проблемы УЧП представлено вектором решения. Решение дает значение в каждой точке mesh каждой зависимой переменной, возможно, в нескольких моментах времени, или соединенный с различными собственными значениями. Векторы решения производятся из mesh, граничных условий и коэффициентов уравнения assempde, pdenonlin, adaptmesh, parabolic, hyperbolic и pdeeig. Опция Export Solution из меню Solve экспортирует решения рабочей области. Поскольку значение вектора решения зависит от своих соответствующих данных о mesh, они всегда используются вместе, когда решение представлено. Для получения дополнительной информации на векторах решения, смотрите страницу с описанием для assempde.
Учитывая пару решения/mesh, множество инструментов обеспечивается для визуализации и обработки данных. pdeintrp и pdeprtni могут использоваться, чтобы интерполировать между функциями, определяемыми при треугольных узлах и функциями, определяемыми при треугольных средних точках. tri2grid интерполирует функции от треугольной mesh до прямоугольной сетки. Используйте pdeInterpolant и evaluate для более общей интерполяции. pdegrad и pdecgrad вычисляют градиенты решения. pdeplot имеет большое количество опций для графического вывода решения. pdecont и pdesurf являются удобными сокращениями для pdeplot.
Используйте средства экспорта приложения PDE Modeler так, как вы можете. Они предоставляют структурам данных правильный синтаксис, и это хорошие отправные точки, которые можно изменить, чтобы удовлетворить потребностям.
Работа с системными матрицами и векторами, произведенными assema и assemb, может иногда быть ценной. При решении того же уравнения для различных загрузок или граничных условий, это платит, чтобы собрать матрицу жесткости только однажды. Точечные нагрузки на конкретном узле могут быть реализованы путем добавления загрузки в соответствующую строку в векторе правой стороны. Нелокальное ограничение может быть включено в матрицы R и H.
Примером рукописного Содействующего файла является circlef.m, который производит точечную нагрузку. Можно найти полный пример в уравнении Пуассона с Точечным источником и Адаптивном Улучшении Mesh и на странице с описанием assempde.
Стандартные программы для адаптивной генерации mesh и решения мощны, но могут привести к плотным сеткам и таким образом долгое время вычисления. При установке параметра Ngen на каждый ограничивает вас одним шагом улучшения. Этот шаг может затем быть повторен, чтобы показать прогресс улучшения. Параметр Maxt помогает вам остановиться, прежде чем адаптивный решатель сгенерирует слишком много треугольников. Примером рукописной треугольной функции выбора является circlepick, используемый в уравнении Пуассона с Точечным источником и Адаптивном Улучшении Mesh. Помните, что вам всегда нужна анализируемая геометрия с adaptmesh.
Деформированные сетки легко построены путем добавления смещений в матрицу Точки p. Принятие двух переменных сохранило в векторе решения u:
np = size(p,2); pdemesh(p+scale*[u(1:np) u(np+1:np+np)]',e,t)
Эволюция времени eigenmodes получена, например,
u1 = u(:,mode)*cos(sqrt(l(mode))*tlist); % hyperbolic
для положительных собственных значений в гиперболических проблемах, или
u1 = u(:,mode)*exp(-l(mode)*tlist); % parabolic
в параболических проблемах. Это делает хорошие анимации, возможно, вместе с деформированными сетчатыми графиками.