Гибкий вал

Вал с крутильным и изгибающимся соответствием

Библиотека:
Simscape / Автомобильная трансмиссия / Couplings & Drives

Описание

Блок Flexible Shaft представляет вал автомобильной трансмиссии с крутильным и изгибающимся соответствием. Вал состоит из гибкого материала, который скручивает в ответ на прикладной крутящий момент и изгибы в ответ на статический массовый дисбаланс. Действие скручивания задерживает механическую передачу между концами вала, изменяя динамический ответ системы автомобильной трансмиссии.

Чтобы представлять гибкий вал скрученности, блок использует модель сосредоточенного параметра. Эта модель делит вал на различные элементы, которые соединяют через параллельные пружинные системы демпфера. Элементы обеспечивают инерцию вала, в то время как пружинные системы демпфера обеспечивают соответствие вала.

Вы задаете инерцию вала, соответствие и количество элементов вала непосредственно в диалоговом окне блока. Выбирая из двух параметризации, можно задать соответствие вала при помощи жесткости и значений затухания или при помощи модуля сдвига вала. Дополнительный параметр позволяет вам смоделировать потери мощности из-за вязкого трения в концах вала. Для получения дополнительной информации см. Крутильную Модель.

Чтобы представлять гибкий вал изгиба, блок использует ваш выбор модели сосредоточенного параметра или eigenmodes модели. В то время как подход сосредоточенного параметра более прост сконфигурировать, подход eigenmodes имеет тенденцию моделировать быстрее. Для получения дополнительной информации об обеих моделях см. Изгибающуюся Модель.

Для модели сосредоточенного параметра количество изгибающихся элементов вала совпадает с количеством элементов вала скрученности, и дополнительные параметры позволяют вам смоделировать линейное затухание, пропорциональное инерции вала и в концах вала. Модель делит вал на различные элементы. Элементы обеспечивают инерцию вала, в то время как матрицы жесткости обеспечивают соответствие вала.

eigenmodes модель вычисляет эффективные массовые пружинные системы демпфера, которые представляют изгибающиеся режимы вала. Можно задать количество режимов, чтобы включать, и дополнительные параметры позволяют вам смоделировать линейное затухание, пропорциональное модальной массе и жесткости.

Для обеих моделей вы задаете соответствие изгиба вала или при помощи изгиба жесткости и линейной массовой плотности или при помощи модуля Янга. Дополнительные параметры включают вам к модели:

Типы монтирования вала. Опции являются идеальным зажимом, контактом, свободным, или жесткость переноса.
Местоположения и инерция или твердых масс точки или дисков, которые присоединены к валу.
Местоположения, значения и угловые смещения статических дисбалансов на вале.

Поскольку два подхода моделирования отличаются, сходимость между ними предоставляет уверенность их результатам. Методические рекомендации должны проверить соглашение для сосредоточенного параметра и eigenmodes ответов при помощи значений параметров из вашей собственной модели гибкого вала в Вале с Крутильным и Поперечным примером Гибкости. Затем для более быстрой симуляции вашей собственной модели используйте подход eigenmodes.

Крутильная модель

Для крутильной модели блок Flexible Shaft аппроксимирует распределенные, непрерывные свойства вала моделью сосредоточенного параметра. Модель содержит конечное число, $N$ , из смешанных ослабленных инерцией пружинных элементов последовательно, плюс итоговая инерция. Результатом является серия $N + 1$ инерция, соединенная $N$ вращательные пружины и $N$ вращательные демпферы.

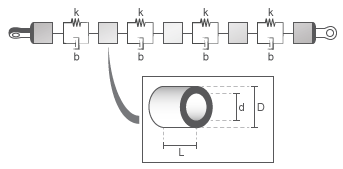
Эквивалентная физическая сеть содержит $N$ сегменты, каждый состоящий из пружины, демпфера и инерции. Сегмент представляет короткий раздел карданного вала, пружина представляет крутильное соответствие, и демпфер представляет существенное затухание. Общая инерция вала разделена в $N + 1$ части, и распределенный равномерно вдоль вала.

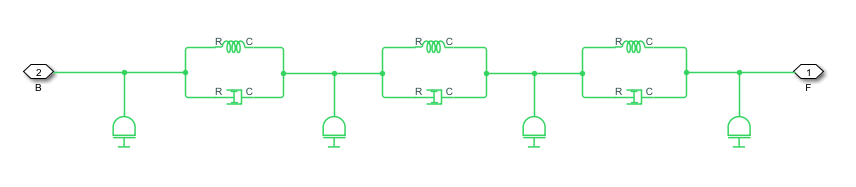
Блок может также включать вязкое трение в концы вала (основа и порты последователя), чтобы представлять несущие убытки в этих точках.

Примечание

Вязкое трение в концах вала отличается от внутреннего существенного затухания, которое соответствует потерям, возникающим в самом материале вала.

Можно параметризовать крутильную модель с помощью или жесткости k и инерцию J или размерностей и свойств материала вала.

Размерности и свойства материала

Жесткость вала и инерция вычисляются из размерностей вала и свойств материала этими отношениями:

$J_{p} = \frac{π}{32} (D^{4} - d^{4})$

$m = \frac{π}{4} (D^{2} - d^{2}) ρ L$

$J = \frac{m}{8} (D^{2} + d^{2}) = ρ L \cdot J p$

$k = J p \cdot \frac{G}{L}$

Где:

_JP является полярным моментом инерции вала.
D является наружным диаметром вала.
d является внутренним диаметром вала. Для твердого вала, $d = 0$ . Для кольцевого вала, $d > 0$ .
L является длиной вала.
m является массой вала.
J является моментом инерции вала.
ρ является плотностью материала вала.
G является модулем сдвига эластичности материала вала.
k является валом вращательная жесткость.

Внутреннее существенное затухание

Для любой крутильной параметризации внутреннее существенное затухание задано отношением затухания, c, для модели одно сегмента. В этом случае крутящий момент затухания $2 \frac{c k}{ω_{N}}$ . Незатухающая собственная частота $ω_{N} = \sqrt{\frac{2 k}{J}}$ . Затухание, примененное через отдельный сегмент сегментированной модели, равно продукту коэффициента затухания и относительной вращательной скорости того сегмента.

Изгиб модели

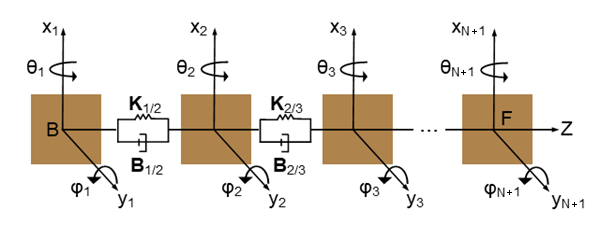
Следующие данные показывают, как измериться:

Статический дисбаланс сместил угол, который является углом статического дисбаланса об оси вала относительно оси x.
Расстояния твердой массы и статического дисбаланса, относительно основы, B.

В фигуре вал зафиксировал поддержки в основе и последователе. Вал проявляет силы, F, и моменты, M, на поддержках. Переводная скорость, V, и вращательная скорость, W, основы и концов последователя относительно их соответствующих поддержек. Все кривые стрелки и соглашения знака следуют за правилом правой руки. Знаки физических сигналов, что блок выходные параметры соответствует стрелкам, которые представляют силы, моменты и скорости вала, действующего на поддержки.

Векторные сигналы:

Сила, Fr = [_Fxb, _Fyb, _Fxf, _Fyf]
Момент, M = [_Mxb, _Myb, _Mxf, _Myf]
Переводная скорость, V = [_Vxb, _Vyb, _Vxf, _Vyf]
Вращательная скорость, W = [_Wxb, _Wyb, Wxf, _Wyf]

Силы вала фиксированной поддержки, моменты и фазы

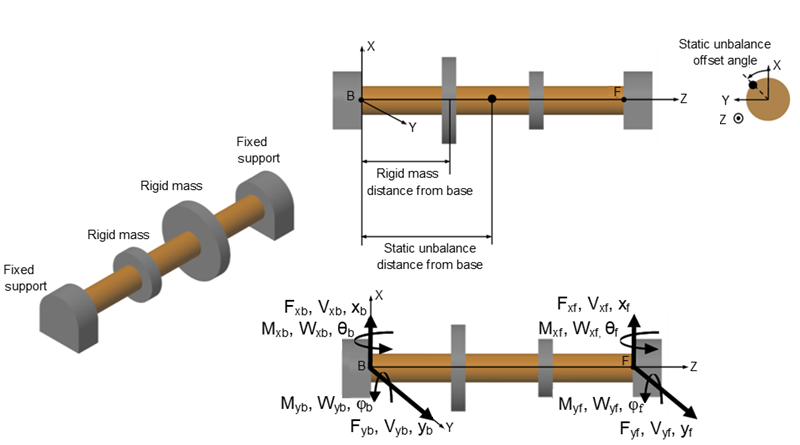
Дифференциальные уравнения с частными производными, управляющие изгибающимся движением вращающегося вала с точками статического массового дисбаланса, могут быть решены с помощью подхода сосредоточенного параметра или подхода eigenmodes. Для обеих моделей существует два определяющих уравнения:

$\frac{\partial^{2}}{\partial z^{2}} (E I \frac{\partial^{2} u_{x}}{\partial z^{2}}) + ρ A \frac{\partial^{2} u_{x}}{\partial t^{2}} = \sum_{j}^{n} m ε_{j} {(Ω (z))}^{2} c o s (φ_{s h a f t} + φ_{o f f s e t, j})$

$\frac{\partial^{2}}{\partial z^{2}} (E I \frac{\partial^{2} u_{y}}{\partial z^{2}}) + ρ A \frac{\partial^{2} u_{y}}{\partial t^{2}} = \sum_{j}^{n} m ε_{j} {(Ω (z))}^{2} s i n (φ_{s h a f t} + φ_{o f f s e t, j})$

Где:

$E I$ жесткость изгиба вала.
$ρ A$ вал линейная массовая плотность.
$m ε_{j}$ $j^{t h}$ статический дисбаланс.
$φ_{o f f s e t, i}$ начальное угловое смещение $j^{t h}$ статический дисбаланс.
$n$ количество статических дисбалансов.
$Ω$ скорость вращения вала.
$φ_{s h a f t}$ мгновенный угол поворота вала.
$z$ координата вдоль оси вала.
$u_{x} (t, z)$ отклонения изгиба вала в перпендикуляре направления x к оси вала.
$u_{y} (t, z)$ отклонения изгиба вала в перпендикуляре направления y к оси вала.

Подход сосредоточенного параметра

Как модель скрученности, подход сосредоточенного параметра для изгибающейся модели дискретизирует распределенные, непрерывные свойства вала в конечное число, $N$ , из сегментов вала. $N$ сегменты вала соответствуют $N + 1$ смешанная инерция, соединенная последовательно путем затухания и пружинные элементы. Однако для изгибающейся модели, каждая масса имеет четыре степени свободы: перевод и вращение и в x и в перпендикуляре направлений y к оси вала.

Уравнение сосредоточенного параметра [1] из движения

$M \ddot{\vec{x}} + B \dot{\vec{x}} + K \vec{x} = \vec{f}$

Где:

$M$ $4 (N + 1) \times 4 (N + 1)$ матрица, которая представляет массу вала.
$\vec{x}$ $4 (N + 1) \times 1$ вектор, который представляет степени свободы для всех узлов, таких что степени свободы для $i^{t h}$ и ${(i + 1)}^{t h}$ узлы

$\vec{x} = [\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} ⋮ \\ \begin{matrix} x_{i} \\ y_{i} \\ θ_{i} \end{matrix} \\ φ_{i} \\ \begin{matrix} \begin{matrix} x_{i + 1} \\ y_{i + 1} \\ θ_{i + 1} \end{matrix} \\ φ_{i + 1} \\ ⋮ \end{matrix} \end{matrix} \end{matrix} \end{matrix} \end{matrix}]$
$K$ $4 (N + 1) \times 4 (N + 1)$ матрица для пружинной жесткости.
$B$ $4 (N + 1) \times 4 (N + 1)$ матрица для постоянного затухания.
$\vec{f}$ $4 (N + 1) \times 1$ вектор, который представляет внешние силы из-за приложения статического массового дисбаланса.

Уравнение для большой матрицы [4]

$M = M_{1 / 2} + M_{2 / 3} + \dots M_{i / i + 1} + \dots M_{N / N + 1} + \sum^{} M_{d i s k, i}$

Где:

$M_{i / (i + 1)}$ большая матрица для отдельного сегмента вала. Для каждого сегмента вала, половины массы и момент инерции передается узлам в обоих концах сегмента. $M_{i / (i + 1)}$ матрица имеет ненулевые элементы в $(4 i - 3) : (4 i + 4)$ строки и $(4 i - 3) : (4 i + 4)$ столбцы:

$M_{i / (i + 1)} = [\begin{matrix} 0 \\ ⋱ \\ \frac{}{12} m & 0000000 \\ 0 & \frac{}{12} m & 000000 \\ 00 & I_{d} & 00000 \\ 000 & I_{d} & 0000 \\ 0000 & \frac{}{12} m & 000 \\ 00000 & \frac{}{12} m & 00 \\ 000000 & I_{d} & 0 \\ 0000000 & I_{d} \\ ⋱ \\ 0 \end{matrix}]$
Где:
- $l$ длина сегмента вдоль оси вала. $l$ зависит от обоих длина вала, $L$ , и количество сегментов, $N$ , таким образом, что $l = \frac{L}{N + 1}$ .
- $m$ масса сегмента. $m$ зависит от внешнего, $D$ , и внутренний, $d$ , диаметры, плотность, $ρ$ , из вала и длины сегмента, такого, что $m = (\frac{π}{4}) (D^{2} - d^{2}) ρ l$ .
- , момент массы полусегмента инерции о перпендикуляре оси к оси вала, зависит от массы и длины сегмента, такого что $I_{d} = m \frac{l^{2}}{24} + \frac{m}{2} {(\frac{l}{2})}^{2}$ .
$\sum^{} M_{d i s k, i}$ суммированные большие матрицы твердых масс, концентрически присоединенных к валу.
Массовые свойства каждой твердой массы, концентрически присоединенной к валу, добавляются к самому близкому узлу, $i$ , таким образом, что

$M_{d i s k, i} ([(4 i - 3) : 4 i], [(4 i - 3) : 4 i]) = [\begin{matrix} M_{d i s k, i} \\ 0000 & M_{d i s k, i} \\ 0000 & I_{D, d i s k, i} \\ 0000 & I_{D, d i s k, i} \end{matrix}]$
где $I_{D, d i s k, i}$ массовый диаметральный момент инерции о перпендикуляре оси к валу для диска.

Уравнение для матрицы затухания

$B = α M + \sum^{} B_{d i s k, i} + [\begin{matrix} b_{B} \\ b_{B} \\ δ_{B} \\ δ_{B} \\ ⋱ \\ b_{F} \\ b_{F} \\ δ_{F} \\ δ_{F} \end{matrix}]$

Где:

$α$ затухание, постоянное пропорциональный массе.
$[b_{B}, b_{F}]$ коэффициенты затухания перевода в основе, B, и последователе, F.
$[δ_{B}, δ_{F}]$ коэффициенты затухания вращения в основе, B, и последователе, F.
$B_{d i s k, i}$ счета на гироскопические эффекты любых концентрически присоединенных дисков, и заданы как

$B_{d i s k, i} ([(4 i - 3) : 4 i], [(4 i - 3) : 4 i]) = [\begin{matrix} 00000000000 & Ω I_{P, d i s k, i} \\ 00 & - Ω I_{P, d i s k, i} & 0 \end{matrix}]$
где $I_{P, d i s k, i}$ массовый полярный момент инерции об оси вала для диска.

Уравнение для матрицы жесткости переноса

$K = K_{B} + K_{1 / 2} + K_{2 / 3} + \dots K_{i / i + 1} + \dots K_{N / N + 1} + K_{F}$

Где:

$K_{i / i + 1}$ матрица жесткости сегмента вала для отдельного сегмента вала. Матрица жесткости для $i^{t h}$ сегмент вала, между $i^{t h}$ и ${(i + 1)}^{t h}$ узлы, имеет ненулевые элементы в $(4 i - 3) : (4 i + 4)$ строки и $(4 i - 3) : (4 i + 4)$ столбцы, такие, что

$K_{i / i + 1} = \frac{2 E I}{l^{3}} [\begin{matrix} 0 \\ ⋱ \\ 600 & 3 l & - 6 & 00 & 3 l \\ 06 & - 3 l & 00 & - 6 & - 3 l & 0 \\ 0 & - 3 l & 2 l^{2} & 00 & 3 l & l^{2} & 0 \\ 3 l & 00 & 2 l^{2} & - 3 l & 00 & l^{2} \\ - 6 & 00 & - 3 l & 600 & - 3 l \\ 0 & - 6 & 3 l & 006 & 3 l & 0 \\ 0 & - 3 l & l^{2} & 00 & 3 l & 2 l^{2} & 0 \\ 3 l & 00 & l^{2} & - 3 l & 00 & 2 l^{2} \\ ⋱ \\ 0 \end{matrix}]$

Где:
- $l$ длина сегмента.
- $E I$ жесткость вала.
$K_{B}$ матрицы жесткости переноса в основе, B, применился к первому узлу, такому что
$K_{B} = [\begin{matrix} K_{B x x} \\ 0000 & K_{B y y} \\ 0000 & K_{B θ θ} \\ 0000 & K_{B φ φ} \end{matrix}]$
Где:
- $[\begin{matrix} K_{B x x} & K_{B y y} \end{matrix}]$ основная переводная жесткость в направлениях y и x.
- $[\begin{matrix} K_{B θ θ} & K_{B φ φ} \end{matrix}]$ основная вращательная жесткость о направлениях y и x.
$K_{F}$ матрицы жесткости переноса в последователе, F, применился к первому и узлу, такому что
$K_{F} = [\begin{matrix} K_{F x x} \\ 0000 & K_{F y y} \\ 0000 & K_{F θ θ} \\ 0000 & K_{F φ φ} \end{matrix}]$
Где:
- $[\begin{matrix} K_{F x x} & K_{F y y} \end{matrix}]$ последователь переводная жесткость в направлениях y и x.
- $[\begin{matrix} K_{F θ θ} & K_{F φ φ} \end{matrix}]$ последователь вращательная жесткость о направлениях y и x

Основа и последователь, переносящий матрицы жесткости, $K_{B}$ и $K_{F}$ , являются ненулевыми, только если вы выбираете Bearing matrix для параметра Base (B) mounting type или параметра Follower (F) mounting type, соответственно. Если вы выбираете тип монтирования Clamped, кинематические условия нулевого вращения и перевода применяются к первым или последним четырем строкам $\vec{x}$ в уравнении сосредоточенного параметра движения. Если вы выбираете тип монтирования Pinned, кинематические условия нулевого перевода применяются к основе узлов последователя в уравнении сосредоточенного параметра движения.

Узел	Монтирование типа	Граничное условие для уравнения сосредоточенного параметра
Основа, B	`Clamped`	$\vec{x} (1 : 4) = 0$
	`Pinned`	$\vec{x} (1 : 2) = 0$
	`Bearing Matrix`	$K_{B} (1 : 4, 1 : 4)$ нетривиальны.
Последователь, F	`Clamped`	$\vec{x} (e n d - 3 : e n d) = 0$
	`Pinned`	$\vec{x} (e n d - 3 : e n d - 2) = 0$
	`Bearing Matrix`	$K_{F} (e n d - 3 : e n d, e n d - 3 : e n d)$ нетривиальны

Внешние силы из-за каждого статического массового дисбаланса прикладываются к самому близкому узлу. Принуждение в $i^{t h}$ узел

${\vec{f}}_{4 (i - 1 : i)} = [\begin{matrix} (m ε_{j, o f f s e t}) Ω_{s h a f t, i}^{2} c o s (φ_{s h a f t, i} + φ_{o f f s e t, j}) \\ (m ε_{j, o f f s e t}) Ω_{s h a f t, i}^{2} s i n (φ_{s h a f t, i} + φ_{o f f s e t, j}) \\ - L_{m ε j} (m ε_{j, o f f s e t}) Ω_{s h a f t, i}^{2} s i n (φ_{s h a f t, i} + φ_{o f f s e t, j}) \\ L_{m ε j} (m ε_{j, o f f s e t}) Ω_{s h a f t, i}^{2} c o s (φ_{s h a f t, i} + φ_{o f f s e t, j}) \end{matrix}]$

Где:

$L_{m ε j}$ расстояние $j^{t h}$ статический дисбаланс от самого близкого $i^{t h}$ узел вдоль оси вала.
$m ε_{j}$ статический дисбаланс.
$φ_{s h a f t, i}$ угол сосредоточенного параметра скрученности для $i^{t h}$ узел.

Подход Eigenmodes

Для подхода eigenmodes блок вычисляет изгибающиеся свойства режима вала в течение времени компиляции и затем моделирует модальные эффективные массовые пружинные системы демпфера с помощью этих шагов:

Определите формы eigenmode путем обработки отклонения каждого сегмента гибкого вала между твердыми массами как пространственная функция с неизвестными коэффициентами:
1. Сгенерируйте уравнения для граничных условий сегмента гибкого вала.
2. Численно решите систему уравнений для модальных частот.
3. Определите форму режима на каждой модальной частоте с помощью нелинейного метода наименьших квадратов.
Примечание
Если вы вводите формы режима непосредственно, блок пропускает этот шаг.
Определите эти динамические свойства для каждого eigenmode:
- Эффективная модальная масса
- Жесткость
- Принуждение коэффициентов
Моделируйте независимые ответы эффективной массовой пружинной системы демпфера для каждого eigenmode.
Получите общий ответ вала путем подведения итогов отклонений каждого eigenmode. Загрузки в поддержках пропорциональны пространственным производным форм режима.

Уравнения для каждого шага в подходе eigenmodes показывают. Для получения информации о деривации уравнений смотрите ^Muszynska[5], Рао ^[6], и Ву ^[7].

Следующие данные показывают углы отклонения и переменные, что использование блока, чтобы решить eigenmodes приближается к уравнениям граничного условия.

Соседние сегменты вала и твердое дисковое движение

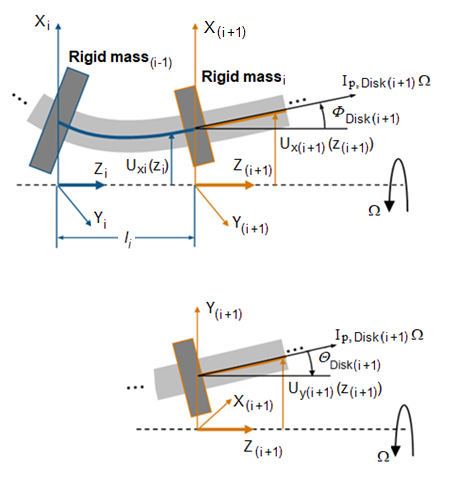
На шаге 1, чтобы решить для eigenmodes, блок рассматривает добровольные уравнения изгиба для луча в этих двух перпендикулярах направлений к оси вала, с помощью этих уравнений:

$\frac{\partial^{2}}{\partial z^{2}} (E I \frac{\partial^{2} u_{x}}{\partial z^{2}}) + ρ A \frac{\partial^{2} u_{x}}{\partial t^{2}} = 0$

$\frac{\partial^{2}}{\partial z^{2}} (E I \frac{\partial^{2} u_{y}}{\partial z^{2}}) + ρ A \frac{\partial^{2} u_{y}}{\partial t^{2}} = 0$

Блок принимает, что решения этих двух уравнений имеют эту форму:

$u_{x} = R e {U_{x} (z) e^{j ω t}} = (A_{x} \sinh (β z) + B_{x} дубинка (β z) + C_{x} \sin (β z) + D_{x} c o s (β z)) R e {e^{j ω t}}$

$u_{y} = R e {U_{y} (z) e^{j ω t}} = (A_{y} \sinh (β z) + B_{y} дубинка (β z) + C_{y} \sin (β z) + D_{y} c o s (β z)) R e {e^{j ω t}}$

$β = {(\frac{ω^{2} ρ A}{E I})}^{1 / 4}$

Где:

$U_{x}$ отклонение формы режима в направлении x.
$U_{y}$ отклонение формы режима в направлении y.
$j = \sqrt{- 1}$ .
$ω$ модальная частота.
$A_{x}, B_{x}, C_{x}, D_{x}, A_{y}, B_{y}, C_{y}, и D_{y}$ коэффициенты.
$E I$ жесткость изгиба вала.
$ρ A$ вал линейная массовая плотность.

В eigenmodes приближаются к уравнениям, $'$ указывает на производную относительно $z$ , ось вдоль вала, такого, что:

$'$ указывает на первую производную относительно $z$ .
$''$ указывает на вторую производную относительно $z$ .
$'''$ указывает на третью производную относительно $z$ .

На шаге 1a, чтобы сгенерировать уравнения для граничных условий сегмента гибкого вала, блок делит вал на $N$ сегменты между валом заканчиваются и $N - 1$ твердые массы присоединяются к валу. Для каждого сегмента блок задает $k^{t h}$ форма режима кусочным способом вдоль целого вала как $U_{k x} (z)$ и $U_{k y} (z)$ .

Для каждого отдельного сегмента вала, $i$ , $k^{t h}$ формы режима, $U_{k x i} (z_{i})$ и $U_{k y i} (z_{i})$ , заданы решениями добровольных уравнений изгиба. Для каждого сегмента вала, $i$ , $z_{i}$ относится к источнику в конце сегмента, самом близком к основе вала, B, концу.

Каждая форма режима сегмента вала имеет восемь неизвестных коэффициентов, $A_{x}, B_{x}, C_{x}, D_{x}, A_{y}, B_{y}, C_{y}, и D_{y}$ . Формы режима $U_{x}$ и $U_{y}$ удовлетворите граничные условия в дисковых интерфейсах и в обоих концах вала.

Граничные условия зависят от монтирующихся типов и применяются к обеим формам режимов. Граничные условия в основном конце вала применяются к первому сегменту. Граничные условия в конце последователя вала применяются к сегменту $N$ .

Уравнения в вале B и концы F

Узел	Монтирование типа	Уравнение граничного условия
Основа, B	`Clamped` — Нулевое отклонение и наклон	$U_{x} (z = 0) = {U^{'}}_{x} (z = 0) = 0$ $U_{y} (z = 0) = {U^{'}}_{y} (z = 0) = 0$
	`Pinned` — Нулевое отклонение и момент	$U_{x} (z = 0) = {U^{″}}_{x} (z = 0) = 0$ $U_{y} (z = 0) = {U^{″}}_{y} (z = 0) = 0$
	`Free` — Нулевой момент и сила	${U^{″}}_{x} (z = 0) = {U^{‴}}_{x} (z = 0) = 0$ ${U^{″}}_{y} (z = 0) = {U^{‴}}_{y} (z = 0) = 0$
	`Bearing Matrix` — С переносом матрицы жесткости $K_{B}$	$K_{B} {\vec{X}}_{b} = K_{B} [\begin{matrix} X_{b} \\ Y_{b} \\ Θ_{b} \\ Φ_{b} \end{matrix}] = K_{B} {[\begin{matrix} U_{x} \\ U_{y} \\ - U_{y}^{'} \\ U_{x}^{'} \end{matrix}] \|}_{z = 0} = E I {[\begin{matrix} - U_{x}^{'''} \\ - U_{y}^{'''} \\ U_{x}^{''} \\ - U_{y}^{''} \end{matrix}] \|}_{z = 0}$ Где: $K_{B} {\vec{X}}_{b}$ пружинная загрузка в основном конце как функция формы режима. $X_{b}, Y_{b}, Θ_{b}, и Φ_{b}$ соответствуйте отклонениям переменных в Силах Вала Фиксированной Поддержки, Моменты и фигура Фаз. $K_{B} = [\begin{matrix} K_{B x x} \\ 0000 & K_{B y y} \\ 0000 & K_{B θ θ} \\ 0000 & K_{B φ φ} \end{matrix}]$
Последователь, F	`Clamped` — Нулевое отклонение и наклон	$U_{x N} (z_{N} = l_{N}) = {U^{'}}_{x N} (z_{N} = l_{N}) = 0$ $U_{y N} (z_{N} = l_{N}) = {U^{'}}_{y N} (z_{N} = l_{N}) = 0$
	`Pinned` — Нулевое отклонение и момент	$U_{x N} (z_{N} = l_{N}) = {U^{″}}_{x N} (z_{N} = l_{N}) = 0$ $U_{y N} (z_{N} = l_{N}) = {U^{″}}_{y N} (z_{N} = l_{N}) = 0$
	`Free` — Нулевой момент и сила	${U^{″}}_{x N} (z_{N} = l_{N}) = {U^{‴}}_{x N} (z_{N} = l_{N}) = 0$ ${U^{″}}_{y N} (z_{N} = l_{N}) = {U^{‴}}_{y N} (z_{N} = l_{N}) = 0$
	`Bearing Matrix` — С переносом матрицы жесткости $K_{F}$	$K_{F} {\vec{X}}_{f} = K_{F} [\begin{matrix} X_{f} \\ Y_{f} \\ Θ_{f} \\ Φ_{f} \end{matrix}] = K_{f} {[\begin{matrix} U_{x} \\ U_{y} \\ - U_{y}^{'} \\ U_{x}^{'} \end{matrix}] \|}_{z = L} = E I {[\begin{matrix} - U_{x}^{'''} \\ - U_{y}^{'''} \\ U_{x}^{''} \\ - U_{y}^{''} \end{matrix}] \|}_{z = L}$ Где: $K_{F} {\vec{X}}_{f}$ пружинная загрузка в конце последователя как функция формы режима $X_{f}, Y_{f}, Θ_{f}, и Φ_{f}$ соответствуйте отклонениям переменных в Силах Вала Фиксированной Поддержки, Моменты и фигура Фаз. $K_{F} = [\begin{matrix} K_{F x x} \\ 0000 & K_{F y y} \\ 0000 & K_{F θ θ} \\ 0000 & K_{F φ φ} \end{matrix}]$

В каждой твердой массе сегмент вала по обе стороны от твердой массы должен удовлетворить непрерывность в смещении и наклоне и равновесии сил и моменты. Чтобы удовлетворить граничные условия, блок использует уравнения в таблице.

Уравнения в твердых массах, концентрически присоединенных к валу

Условие	Твердые массы концентрически присоединяются к валу
	Масса точки	Диск
Непрерывность смещения	$U_{x i} (l_{i}) = U_{x (i + 1)} (0)$ $U_{y i} (l_{i}) = U_{y (i + 1)} (0)$
Наклонная непрерывность	${U^{'}}_{x i} (l_{i}) = - {U^{'}}_{x (i + 1)} (0)$ ${U^{'}}_{y i} (l_{i}) = - {U^{'}}_{y (i + 1)} (0)$
Обеспечьте баланс	$- ω^{2} M_{d i s k, i} U_{x i} (l_{i}) = E I {U^{‴}}_{x i} (l_{i}) - E I {U^{‴}}_{x (i + 1)} (0)$ $- ω^{2} M_{d i s k, i} U_{y i} (l_{i}) = E I {U^{‴}}_{y i} (l_{i}) - E I {U^{‴}}_{y (i + 1)} (0)$
Баланс момента	$0 = - E I {U^{″}}_{x i} (l_{i}) + E I {U^{″}}_{x (i + 1)} (0)$ $0 = - E I {U^{″}}_{y i} (l_{i}) + E I {U^{″}}_{y (i + 1)} (0)$	$- ω^{2} I_{D, d i s k, i} Θ - j ω Ω_{s h a f t} I_{P, d i s k, i} Φ_{d i s k (i + 1)} = - E I {U^{″}}_{y i} (l_{i}) + E I {U^{″}}_{y (i + 1)} (0)$ $- ω^{2} I_{D, d i s k, i} Φ + j ω Ω_{s h a f t} I_{P, d i s k, i} Θ_{d i s k (i + 1)} = - E I U^{' '}_{x i} (l_{i}) + E I {U^{″}}_{x (i + 1)} (0)$

Переменные для уравнений в этой таблице:

$Ω_{s h a f t}$ номинальная скорость вращения вала в средней точке вала.
$I_{P, d i s k, i}$ твердый массовый полярный момент инерции об оси вала.
$ω$ модальная частота.
$I_{d, d i s k, i}$ твердый массовый диаметральный момент инерции об оси вала.
$E I$ жесткость изгиба вала.
$j = \sqrt{- 1}$

На шаге 1b блок численно решает для модальных частот путем объединения граничных условий сегмента вала в вале B и концах F с граничными условиями сегмента вала в твердых массах, концентрически присоединенных к валу. Получившееся уравнение, в матричной форме,

$H (ω) \vec{S} = 0$

Где:

$\vec{S}$ содержит модальные коэффициенты для $N$ сегменты вала, такие, что

$\vec{S} = [\begin{matrix} A_{x 1} \\ B_{x 1} \\ C_{x 1} \\ D_{x 1} \\ A_{y 1} \\ B_{y 1} \\ C_{y 1} \\ D_{y 1} \\ \begin{matrix} ⋮ \\ A_{x N} \\ B_{x N} \\ C_{x N} \\ D_{x N} \\ A_{y N} \\ B_{y N} \\ C_{y N} \\ D_{y N} \end{matrix} \end{matrix}]$

Для нетривиальных модальных решений должна удовлетворить система уравнений $| H (ω) | = 0$ .

Определить модальные решения для частоты численно, блок:

Вычисляет начальные решения для собственной частоты, $ω_{k I N I T I A L}$ , путем взятия локальных минимумов $a b s (| H (ω) |)$ $ω = [0 : d ω : ω_{M a x}]$ , где:
- $d ω$ разрешение поиска собственной частоты.
- $ω_{\max}$ максимальная рассмотренная собственная частота.
Блок совершенствовал каждого $ω_{k}_{I N I T I A L}$ заменяя его на минимум $a b s (| H (ω) |)$ $ω = ω_{k}_{I N I T I A L} + d ω ([- 1 : d ω_{R e f i n e F a c t o r} : 1])$

Блок затем использует нелинейный метод наименьших квадратов, чтобы определить коэффициенты формы режима $\vec{S}$ на каждой модальной частоте.

На шаге 2 блок определяет эти eigenmode свойства динамики:

Модальная масса
Модальная жесткость
Модальное затухание
Модальные коэффициенты принуждения

Блок уменьшает динамику каждого режима, $k$ , к независимой системе уравнений:

$M_{k x} {\ddot{η}}_{k x} + B_{k d x} {\dot{η}}_{k x} + B_{k p y} {\dot{η}}_{k y} + K_{k x} η_{k x} = f_{k x}$

$M_{k y} {\ddot{η}}_{k y} + B_{k d y} {\dot{η}}_{k y} + B_{k p x} {\dot{η}}_{k x} + K_{k y} η_{k y} = f_{k y}$

Где:

$η_{k x}$ зависящий от времени коэффициент $k^{t h}$ режим в $x$ направление.
$η_{k y}$ зависящий от времени коэффициент $k^{t h}$ режим в $y$ направление.

Уравнения для $k^{t h}$ модальная масса:

$M_{k x} = \int_{0}^{L} ρ A U_{k x}^{2} d z + \sum^{} M_{d i s k, i} {U_{k x}^{2} |}_{z d i s k, i} + \sum^{} I_{D, d i s k, i} {{U^{'}}_{k x}^{2} |}_{z d i s k, i}$

$M_{k y} = \int_{0}^{L} ρ A U_{k y}^{2} d z + \sum^{} M_{d i s k, i} {U_{k y}^{2} |}_{z d i s k, i} + \sum^{} I_{D, d i s k, i} {{U^{'}}_{k y}^{2} |}_{z d i s k, i}$

Уравнения для $k^{t h}$ модальная жесткость:

$K_{k x} = \int_{0}^{L} E I {U^{″}}_{k x}^{2} d z + \sum^{} {U_{k x} |}_{z = 0} K_{B} ([1, 4], :) {\vec{X}}_{k b} + \sum^{} {U_{k x} |}_{z = l} K_{F} ([1, 4], :) {\vec{X}}_{k f}$

$K_{k y} = \int_{0}^{L} E I {U^{″}}_{k y}^{2} d z + \sum^{} {U_{k y} |}_{z = 0} K_{B} ([2, 3], :) {\vec{X}}_{k b} + \sum^{} {U_{k y} |}_{z = l} K_{F} ([2, 3], :) {\vec{X}}_{k f}$

Где:

L является длиной вала.
$K_{B}$ и $K_{F}$ только используются, когда контур вала задан матрицей переноса.
Только строки, которые способствуют загрузке в каждом модальном направлении, играют роль в модальном выражении жесткости того направления.

Уравнения для модального затухания из-за диска полярный момент инерции:

$D_{k p x} = - Ω_{s h a f t} \sum^{} I_{P, d i s k} (Φ_{k} Θ_{k}) |_{z d i s k}$

$D_{k p y} = Ω_{s h a f t} \sum^{} I_{P, d i s k} (Φ_{k} Θ_{k}) |_{z d i s k}$

Уравнения для диссипативного модального затухания:

$D_{k d x} = α M_{k x} + β K_{k x}$

$D_{k d y} = α M_{k y} + β K_{k y}$

Где:

$α$ затухание, постоянное пропорциональный массе.
$β$ затухание, постоянное пропорциональный жесткости.

Уравнения для модального принуждения из-за массовых статических дисбалансов:

$f_{k x} = Ω_{s h a f t}^{2} \sum^{} (m ε_{o f f s e t, j}) U_{k x} (z_{o f f s e t, j}) потому что (φ_{s h a f t} + φ_{o f f s e t, j})$

$f_{k y} = Ω_{s h a f t}^{2} \sum^{} (m ε_{o f f s e t, j}) U_{k y} (z_{o f f s e t, j}) \sin (φ_{s h a f t} + φ_{o f f s e t, j})$

Где:

Силы каждого статического дисбаланса, $j$ , суммированы для общей силы на $k^{t h}$ режим.
$Ω_{s h a f t}$ мгновенная скорость вращения в средней точке вала.
$φ_{s h a f t}$ мгновенный угол в средней точке вала.
$φ_{o f f s e t, j}$ начальный угол excitational $j^{t h}$ статический дисбаланс.

На шаге 4 блок суммирует отклонения каждого eigenmode, чтобы получить общий ответ вала. Уравнения для общего мгновенного отклонения вдоль вала:

$u_{x} (t, z) = \sum^{} U_{k x} (z) η_{k x} (t)$

$u_{y} (t, z) = \sum^{} U_{k y} (z) η_{k y} (t)$

Уравнения для мгновенной силы, действующей на поддержки в вале B и концы F в x и направлениях y:

$F_{x b} = - E I \sum^{} {U_{k x}^{'''} |}_{z = 0} η_{k x} (t)$

$F_{y b} = - E I \sum^{} {U_{k y}^{'''} |}_{z = 0} η_{k y} (t)$

$F_{x f} = E I \sum^{} {U_{k x}^{'''} |}_{z = l} η_{k x} (t)$

$F_{y f} = E I \sum^{} {U_{k y}^{'''} |}_{z = l} η_{k y} (t)$

Уравнения в течение мгновенного момента, действуя на поддержки в концах вала:

$M_{x b} = E I \sum^{} {U_{k x}^{''} |}_{z = 0} η_{k x} (t)$

$M_{y b} = - E I \sum^{} {U_{k y}^{''} |}_{z = 0} η_{k y} (t)$

$M_{x f} = - E I \sum^{} {U_{k x}^{''} |}_{z = l} η_{k x} (t)$

$M_{y f} = E I \sum^{} {U_{k y}^{''} |}_{z = l} η_{k y} (t)$

Улучшите скорость симуляции или точность

Чтобы увеличить точность симуляции для подхода сосредоточенного параметра для крутильной или изгибающейся модели, увеличьте число сегментов. Однако как количество увеличений сегментов, производительность симуляции, которая является скоростью симуляции, может уменьшиться. Одно сегментированная крутильная модель показывает собственную частоту, которая является близко к первой собственной частоте непрерывной модели распределенного параметра.

Для большей точности можно выбрать 2, 4, 8, или больше сегментов. Например, четыре самых низких крутильных собственных частоты представлены с точностью до 0,1, 1.9, 1.6, и 5,3 процентов, соответственно, 16 сегментированной моделью.

Чтобы увеличить точность симуляции для eigenmodes приближаются к изгибающейся модели:

Проверьте, что параметр Nominal shaft speed for bending modes близко к скорости вала симуляции. Этот параметр может влиять на образцовые результаты, если вы параметризовали твердую массу, присоединенную к валу с большим массовым моментом инерции об оси вала.
Уменьшите значения параметров Eigenfrequency refine factor и Eigenfrequency search resolution. Сокращение этих значений может увеличить точность модальных частот и форм.
Уменьшите константы затухания. Вычисления Simscape™ модальных свойств перед симуляцией не составляют затухание.
Подкачайте значения для основы, B и последователя, F, параметров граничного условия и инвертируйте блок в модели Simscape. Формы Eigenmodes зависят от функций дубинки и sinh. Поэтому ошибки могут произойти около конца F.
Проверяйте чувствительность к параметрам Advanced Bending при помощи ваших параметров в модели гибкого вала в Вале с Крутильным и Поперечным примером Гибкости. Настройте параметры и используйте ссылки, обеспеченные в примере, чтобы исследовать, как значения влияют на eigenmode частоты и формы. Настройте значения параметров в своей модели соответственно.
Увеличьте значения параметров Limit number of modes и Eigenfrequency upper limit. Самая высокая модальная частота в симуляции должна быть достаточно больше, чем частота вращения вала.

Ограничения и предположения

Модель распределенного параметра непрерывного крутильного вала аппроксимирована конечным числом, $N$ , из сосредоточенных параметров.
Гибкий вал имеет постоянное осесимметричное поперечное сечение вдоль своей длины.
Вращение вала и гибкость скрученности волнуют изгиб вала, но изгиб не влияет на вращение вала и гибкость скрученности.
Твердые массы точки или диски, присоединенные к валу, имеют тонкие длины, параллельные оси вала.
Для eigenmodes изгибающаяся модель затухание не влияет на собственные частоты.
Переносящие поддержки расположены в конечных точках вала.
Изгиб вала не передается между блоками Гибкого вала.
Относительно длины вала наружный диаметр вала является небольшим. Отношение длины вала к наружному диаметру больше, чем 20.
Относительно длины вала изгибающееся отклонение является маленьким.
Статические массовые дисбалансы являются единственными изгибающими вал внешними увлекательными загрузками.
Поддержки вала являются стационарными.
Гироскопические эффекты твердых дисков рассматриваются; пропускают гироскопическими эффектами самого вала.
Статическое массовое принуждение дисбаланса в подходе eigenmodes использует скорость вращения в средней точке вала.
Чтобы удовлетворить режим вала формируют проблему граничных условий, блок использует алгоритм Levenberg-Marquardt.

Порты

Вывод

развернуть все

`Fr` — Обеспечьте при переносе поддержек
физический сигнал

Выходной порт физического сигнала сопоставил с силой, которую вал проявляет на поддержках переноса.

`M` Момент при переносе поддержек
физический сигнал

Выходной порт физического сигнала сопоставил с моментом, который вал проявляет на поддержках переноса.

`V` Вал переводная скорость
физический сигнал

Выходной порт физического сигнала сопоставлен с переводной скоростью вала в поддержках переноса.

`W` Вал угловая скорость
физический сигнал

Выходной порт физического сигнала сопоставлен с угловой скоростью вала в поддержках переноса.

Сохранение

развернуть все

`B` Основа
вращательное механическое устройство

Вращательный порт сохранения сопоставлен с основой вала.

`F` Последователь
вращательное механическое устройство

Вращательный порт сохранения сопоставлен с последователем вала.

Параметры

развернуть все

Вал

Таблица показывает, как видимость некоторых параметров зависит от опции, которую вы выбираете для других параметров. Чтобы изучить, как считать таблицу, смотрите Зависимости от Параметра.

Зависимости от параметра вала

Shaft
Изгиб модели — Выбирает `Off` или `On`
'off'			На
			Представляет выходные порты блока: Fr M V W
			Представляет параметры для: Bending Advanced Bending
Параметризация — выбирает `By stiffness and inertia` или `By material properties`
Жесткостью и инерцией	Свойствами материала		Жесткостью и инерцией	Свойствами материала
Количество сегментов
Крутильная жесткость	Длина вала		Крутильная жесткость	Длина вала
Крутильная инерция	Геометрия вала — Выбирает `Solid` или `Annular`		Крутильная инерция	Геометрия вала — Выбирает `Solid` или `Annular`
	Тело	Кольцевой	Длина вала	Тело	Кольцевой
	Наружный диаметр вала		Изгиб жесткости	Наружный диаметр вала
	-	Вал внутренний диаметр	Линейная плотность		Вал внутренний диаметр
	Существенная плотность			Существенная плотность
	Сдвиньте модуль			Сдвиньте модуль
	Сдвиньте модуль			Модуль молодежи

Опция модели `Model bending` — Bending
`Off` (значение по умолчанию) | `On`

Опция к образцовому изгибу.

Зависимости

Установка параметра Model bending на On представляет эти порты и параметры, которые скрыты по умолчанию:

Выходной порт Fr
Выходной порт M
Выходной порт V
Выходной порт W
Параметры Advanced Bending
Параметры Bending

Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

`Parameterization` — Метод параметризации
`By stiffness and inertia` (значение по умолчанию) | `By material properties`

Метод параметризации.

Зависимости

Каждая опция Parameterization представляет связанные параметры и скрывает несвязанные параметры. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

`Number of segments` — Количество сегментов вала
`1` (значение по умолчанию) | положительное целое число

Количество сегментов, $N$ , для приближения.

Большее число сегментов, $N$ , увеличивает точность модели, но уменьшает производительность симуляции, то есть, скорость симуляции. Одно сегментированная модель ( $N$ =1) показывает собственную частоту скрученности, которая является близко к первой собственной частоте непрерывной модели распределенного параметра.

Если точность более важна, чем производительность, выберите 2, 4, 8, или больше сегментов. Например, четыре самых низких собственных частоты скрученности представлены с точностью до 0,1, 1.9, 1.6, и 5,3 процентов, соответственно, 16 сегментированной моделью. Точно моделирование изгибающейся динамики обычно требует большего количества сегментов, чем динамика скрученности.

`Torsional stiffness` — Существенная жесткость
`2e5` `N*m/rad` (значение по умолчанию) | положительная скалярная величина

Существенная жесткость.

Зависимости

Установка параметра Model bending на Off и параметра Parameterization к By stiffness and inertia или установка параметра Model bending на On представляют этот параметр. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

`Torsional Inertia` — Инерция вала
`0.02` `kg*m^2` (значение по умолчанию) | положительная скалярная величина

Инерция вала.

Зависимости

Установка параметра Parameterization на By stiffness and inertia представляет этот параметр. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

`Shaft length` — Длина вала
`1` `m` (значение по умолчанию) | положительная скалярная величина

Длина вала.

Зависимости

Этот параметр видим, когда вы устанавливаете параметр Model bending на Off и параметр Parameterization к By stiffness and inertia или когда вы устанавливаете параметр Model bending на On. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

`Bending rigidity` — Изгиб жесткости
`5e5` `m^4*Pa` (значение по умолчанию) | положительная скалярная величина

Изгиб жесткости для материала вала.

Зависимости

Установка параметра Model bending на On и параметра Parameterization к By stiffness and inertia представляет этот параметр. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

`Linear density` — Линейная плотность
`19` `kg/m` (значение по умолчанию) | положительная скалярная величина

Линейная плотность для материала вала.

Зависимости

`Shaft geometry` — Поперечное сечение вала
`Solid` (значение по умолчанию) | `Annular`

Вал перекрестная частная геометрия.

Зависимости

Установка параметра Parameterization на By material properties представляет этот параметр. Каждая опция Shaft geometry представляет другие параметры. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

`Shaft outer diameter` — Наружный диаметр вала
`0.075` `m` (значение по умолчанию) | положительная скалярная величина

Наружный диаметр вала.

Зависимости

Установка параметра Parameterization на By material properties представляет этот параметр. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

`Shaft inner diameter` — Вал внутренний диаметр
`0.05` `m` (значение по умолчанию) | положительная скалярная величина

Вал внутренний диаметр. Если вал тверд, задайте 0.

Зависимости

Установка параметра Parameterization на By material properties и параметра Shaft geometry к Annular представляет этот параметр. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

`Material density` — Существенная плотность
`7.8e3` `kg/m^3` (значение по умолчанию) | положительная скалярная величина

Существенная плотность.

Зависимости

`Shear modulus` — Сдвиньте модуль
`7.93e9` `Pa` (значение по умолчанию) | положительная скалярная величина

Сдвиньте модуль для материала вала.

Зависимости

`Young's modulus` — Модуль молодежи
`200e9` `Pa` (значение по умолчанию) | положительная скалярная величина

Модуль молодежи для материала.

Зависимости

Установка параметра Model bending на On и параметра Parameterization к By material properties представляет этот параметр. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

Скрученность

`Damping ratio from internal losses` — Материальное отношение затухания
`0.01` (значение по умолчанию) | положительная скалярная величина

Материальное отношение затухания.

`Viscous friction coefficients at base (B) and follower (F)` — Вязкие коэффициенты трения
`[0, 0]` `N*m/(rad/s)` (значение по умолчанию) | неотрицательный вектор

Вязкие коэффициенты трения в основном порте, B, и порте последователя, F.

Изгиб

Параметры Bending представлены только, когда параметр Shaft Model bending устанавливается на On. Для получения дополнительной информации смотрите Зависимости от Параметра Вала. Видимость некоторых параметров Bending также зависит от опции, что вы выбираете для параметра Advanced Bending Bending vibration analysis method.

Изгиб зависимостей от параметра

Bending
Основа (B) монтирующий тип — Выбирает `Clamped`, `Pinned`, `Free` или `Bearing matrix`
Зафиксированный, прикрепленный, или свободный		Перенос матрицы
		Основа (B) переводная жесткость [x y
		Основа (B) вращательная жесткость [x y
Последователь (F) монтирующий тип — Выбирает `Clamped`, `Pinned`, `Free` или `Bearing matrix`
Зафиксированный, прикрепленный, или свободный		Перенос матрицы
		Последователь (F) переводная жесткость [x y
		Последователь (F) вращательная жесткость [x y
Затухание постоянного пропорциональный массе
Затухание постоянного пропорциональный жесткости
Коэффициент затухания перевода в основе (B) и последователь (F) *
Коэффициент затухания вращения в основе (B) и последователь (F) *
Затухание постоянного пропорциональный жесткости **
Твердые массы, концентрически присоединенные к валу — Выбирают `None`, `Point mass` или `Disk`
'none'	Масса точки	Диск
	Твердые массовые местоположения вдоль вала (расстояние от узла B)
	Твердые массы
	-	Твердые массовые диаметральные моменты инерции о перпендикуляре оси к валу
	-	Твердые массовые полярные моменты инерции об оси вала
Статические дисбалансы, которые волнуют изгиб
Статические расстояния дисбаланса от основы (B)
Статический дисбаланс сместил угол

* Этот параметр видим только, когда параметр Advanced Bending Bending vibration analysis method устанавливается на Lumped

** Этот параметр видим только, когда параметр Advanced Bending Bending vibration analysis method устанавливается на Eigenmodes

`Base (B) mounting type` — Базовый тип монтирования
`Clamped` (значение по умолчанию) | `Pinned` | `Free` | `Bearing matrix`

Тип монтирования в основном конце вала.

Зависимости

Этот параметр видим только, когда параметр Shaft Model bending устанавливается на On. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

Установка этого параметра на Bearing matrix представляет связанные параметры. Для получения дополнительной информации смотрите Изгибающиеся Зависимости от Параметра.

`Base (B) translational stiffness [x y]` — Основывайте переводную жесткость
`[10e7 10e7]` `N/m` (значение по умолчанию) | неотрицательный вектор

Переводная жесткость для монтирования в основном конце вала, $[\begin{matrix} K_{B x x} & K_{B y y} \end{matrix}]$ . Первый элемент является жесткостью поддержки в направлении x. Второй элемент является жесткостью поддержки в направлении y.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On и параметр Bending Base (B) mounting type, устанавливается на Bearing matrix. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и Изгибающиеся Зависимости от Параметра.

`Base (B) rotational stiffness [x y]` — Основывайте вращательную жесткость
`[10e5 10e5]` `N*m/rad` (значение по умолчанию) | неотрицательный вектор

Вращательная жесткость для монтирования в основном конце вала, $[\begin{matrix} K_{B θ θ} & K_{B φ φ} \end{matrix}]$ . Первый элемент является жесткостью поддержки о направлении x. Второй элемент является жесткостью поддержки о направлении y.

Зависимости

`Follower (F) mounting type` — Последователь, монтирующий тип
`Clamped` (значение по умолчанию) | `Pinned` | `Free` | `Bearing matrix`

Тип монтирования в конце последователя вала.

Зависимости

`Follower (F) translational stiffness [x y]` — Последователь переводная жесткость
`[10e7 10e7]` `N/m` (значение по умолчанию) | неотрицательный вектор

Переводная жесткость для монтирования в конце последователя вала, $[\begin{matrix} K_{F x x} & K_{F y y} \end{matrix}]$ . Первый элемент является жесткостью поддержки в направлении x. Второй элемент является жесткостью поддержки в направлении y.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On и параметр Bending Follower (F) mounting type, устанавливается на Bearing matrix. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и Изгибающиеся Зависимости от Параметра.

`Follower (F) rotational stiffness [x y]` — Последователь вращательная жесткость
`[10e5 10e5]` `N*m/rad` (значение по умолчанию) | неотрицательный вектор

Вращательная жесткость для монтирования в конце последователя вала, $[\begin{matrix} K_{F θ θ} & K_{F φ φ} \end{matrix}]$ . Первый элемент является жесткостью поддержки о направлении x. Второй элемент является жесткостью поддержки о направлении y.

Зависимости

`Damping constant proportional to mass` — Ослабляя постоянный, a
`10` `1/s` (значение по умолчанию) | положительная скалярная величина

Ослабляя постоянный, a, пропорциональный массе.

Когда eigenmodes, который изгибающаяся модель включена, демпфер перевода в каждой модальной массовой пружинной системе демпфера, имеет коэффициент затухания _aMMode, где _MMode является модальной массой.

Когда модель изгиба сосредоточенного параметра включена, каждый смешанный массовый элемент имеет перевод, ослабляющий коэффициент _aMelement и вращение, ослабляющее коэффициент _aIelement. _Melement является объединенной массой смешанного массового элемента вала и твердой массой точки или диском, если твердая масса точки или диск присоединены к тому элементу. _Ielement является объединенным массовым моментом инерции смешанного массового элемента вала и твердого диска, если твердый диск присоединен к тому элементу.

Зависимости

`Translation damping coefficient at base(B) and follower(F)` — Коэффициент затухания перевода
`[0, 0]` `N/(m/s)` (значение по умолчанию) | неотрицательный вектор

Затухание коэффициентов для демпфера, который действует на движение перевода вала в основе и последователе.

Первый элемент для затухания в основе, и второй элемент для затухания в последователе. X и направления Y имеют то же затухание.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On и параметр Shaft Bending vibration analysis method, устанавливается на Lumped mass. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и Изгибающиеся Зависимости от Параметра.

`Rotation damping coefficient at base(B) and follower(F)` — Коэффициент затухания вращения
`[0, 0]` `N*m/(rad/s)` (значение по умолчанию) | неотрицательный вектор

Затухание коэффициента для демпфера, который действует на движение вращения вала в основе и концах последователя и в X и в направлениях Y. Первый элемент для затухания в основе, и второй элемент для затухания в последователе. X и направления Y имеют то же затухание.

Зависимости

`Damping constant proportional to stiffness` — Ослабляя постоянный, b
`1e-8` `s` (значение по умолчанию) | положительная скалярная величина

Когда eigenmodes, который изгибающаяся модель включена, демпфер перевода в каждой модальной массовой пружинной системе демпфера, имеет коэффициент затухания _bKMode, где _KMode является модальной жесткостью.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On и параметр Shaft Bending vibration analysis method, устанавливается на Eigenmodes. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и Изгибающиеся Зависимости от Параметра.

`Rigid masses concentrically attached to shaft` — Тип твердых масс присоединяется к валу
`None` (значение по умолчанию) | `Point mass` | `Disk`

Введите, если таковые имеются, твердых масс, присоединенных к валу.

Зависимости

Установка этого параметра на Point mass или Disk представляет связанные параметры. Для получения дополнительной информации смотрите Изгибающиеся Зависимости от Параметра.

`Rigid mass locations along shaft (distance from B node)` — Твердые массовые местоположения вдоль вала в расстоянии от основного узла
`0.5` `m` (значение по умолчанию) | неотрицательный скаляр или вектор

Твердые массовые местоположения вдоль вала в расстоянии от основного узла. Для нескольких масс задайте вектор - строку.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On и параметр Bending Rigid masses attached to shaft, устанавливается на Point mass. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и Изгибающиеся Зависимости от Параметра.

`Rigid masses` — Масса твердых масс концентрически присоединяется к валу
`2` `kg` (значение по умолчанию) | неотрицательный скаляр или вектор

Масса твердых масс концентрически присоединяется к валу. Для нескольких масс задайте вектор - строку.

`Rigid mass diametric moments of inertia about axis perpendicular to shaft` — Диаметральные моменты инерции о перпендикуляре оси к валу
`0.025` `kg*m^2` (значение по умолчанию) | неотрицательный скаляр или вектор

Твердые массовые моменты инерции о перпендикуляре оси к валу. Для нескольких масс задайте вектор - строку.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On и параметр Bending Rigid masses attached to shaft, устанавливается на Disk. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и Изгибающиеся Зависимости от Параметра.

`Rigid mass polar moments of inertia about shaft axis` — Полярные моменты инерции об оси вала
`0.050` `kg*m^2` (значение по умолчанию) | неотрицательный скаляр или вектор

Твердые полярные массовые моменты инерции о перпендикуляре оси к валу.

Зависимости

`Static unbalances that excite bending` — Excitational статические дисбалансы
`[.01, .01]` `m*kg` (значение по умолчанию) | неотрицательный вектор

Статические дисбалансы, которые волнуют изгиб.

Зависимости

`Static unbalance distances from base (B)` — Статические расстояния дисбаланса от основы
`[.33, .67]` `m` (значение по умолчанию) | неотрицательный вектор

Расстояние excitational статических дисбалансов от основы, конца B вала.

Зависимости

`Static unbalance offset angles` — Статический дисбаланс сместил углы
`[0, pi]` `rad` (значение по умолчанию) | неотрицательный вектор

Начальный угол, о средней линии вала относительно x - ось, excitational статических дисбалансов.

Зависимости

Усовершенствованный изгиб

Параметры Advanced Bending представлены только, когда параметр Shaft Model bending устанавливается на On. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.

Усовершенствованные зависимости от параметра изгиба

Advanced Bending
Изгиб метода анализа вибрации — Выбирает `Lumped mass` или `Eigenmodes` Опция, которую вы выбираете для этого параметра, влияет на видимость некоторых параметров Bending. Для получения дополнительной информации смотрите Зависимости от Параметра Вала.
Смешанная масса	Eigenmodes
	Изгиб определения режима — Выбирает `Simscape determined` или `User defined`
	Simscape определяется	Определяемый пользователем
	Ограничьте количество режимов	Определяемый пользователем
	Номинальная скорость вала для изгиба режимов
	Начальная буква собственной частоты ищет разрешение	Модальные частоты
	Собственная частота совершенствовала фактор	Положение вала
	Верхний предел собственной частоты	Матрица формы режима
	Длина вала постепенно увеличивается для вычислений формы режима	Матрица формы режима

`Bending vibration analysis method` — Изгиб метода анализа вибрации
`Lumped mass` (значение по умолчанию) | `Eigenmodes`

Метод для анализа изгибающейся вибрации.

Зависимости

Установка этого параметра на Eigenmodes представляет, связал параметры Advanced Bending. Для получения дополнительной информации смотрите Усовершенствованные Зависимости от Параметра Изгиба.

Опция, которую вы выбираете для этого параметра также, влияет на видимость некоторых параметров Bending. Для получения дополнительной информации смотрите Изгибающиеся Зависимости от Параметра.

Метод определения режима `Bending mode determination` — Bending
`Simscape determined` (значение по умолчанию) | `User defined`

Опция, чтобы иметь Simscape определяет eigenmode частоты и формы или задавать изгибающиеся частоты режима и формы с помощью параметров, которые вы задаете.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On и параметр Advanced Bending Bending vibration analysis method, устанавливается на Eigenmodes. Каждая опция для этого параметра представляет связанные параметры и скрывает несвязанные параметры. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и Усовершенствованные Зависимости от Параметра Изгиба.

`Limit number of modes` — Максимальное количество режимов
`6` (значение по умолчанию) | положительный целочисленный скаляр

Максимальное количество режимов, которые определяет Simscape.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On, параметр Advanced Bending Bending vibration analysis method, устанавливается на Eigenmodes и параметр Advanced Bending, Bending mode determination установлен в Simscape determined. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и Усовершенствованные Зависимости от Параметра Изгиба.

`Nominal shaft speed for bending modes` — Номинальная скорость вала для изгиба режимов
`100` `rpm` (значение по умолчанию) | неотрицательный скаляр

Номинальная скорость вала для изгиба режимов.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On и параметр Advanced Bending Bending vibration analysis method, устанавливается на Eigenmodes. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и Усовершенствованные Зависимости от Параметра Изгиба.

`Eigenfrequency initial search resolution` — Разрешение поиска собственной частоты
`5` `rad/s` (значение по умолчанию) | положительный целочисленный скаляр

Начальное разрешение для поиска собственной частоты.

Алгоритм для определения собственных частот рассматривает значения [0:dɷ:ɷMax] как возможные собственные частоты, где dɷ является разрешением поиска собственной частоты, и _ɷMax является eigengrequency верхним пределом.

Зависимости

`Eigenfrequency refine factor` — Фактор улучшения собственной частоты
`1e-4` `rad/s` (значение по умолчанию) | неотрицательный скаляр

Фактор улучшения для разрешения для поиска собственной частоты.

Для каждой собственной частоты _ɷkINITIAL, который найден с помощью разрешения поиска собственной частоты, алгоритм, совершенствовал со значением собственной частоты путем повторения процедуры решения при рассмотрении _ɷkINITIAL +dɷ* _{[-1:dɷRefineFactor:1}] как возможные собственные частоты. Эта процедура улучшения может быть важна для получения правильной формы eigenmode.

Зависимости

`Eigenfrequency upper limit` — Верхний предел собственной частоты
`50000` `rad/s` (значение по умолчанию) | положительный целочисленный скаляр

Верхний предел собственной частоты.

Зависимости

`Shaft length increments for mode shape computations` — Шаг длины вала
`0.01` `m` (значение по умолчанию) | положительная скалярная величина

Шаг длины вала используется для массы режима и вычислений формы.

Формы режима заданы на расстояниях от основы, [0:dz:L], где L является длиной вала. Эти векторы формы режима численно интегрированы, чтобы определить модальную массу, жесткость и затухание.

Зависимости

`Modal frequencies` — Модальные частоты
`[162, 162, 649, 649, 1460, 1460, 2596, 2596]` `rad/s` (значение по умолчанию) | вектор

Модальные частоты.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On, параметр Advanced Bending Bending vibration analysis method, устанавливается на Eigenmodes и параметр Advanced Bending, Bending mode determination установлен в User defined. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и Усовершенствованные Зависимости от Параметра Изгиба.

`Shaft position` — Положение вала
`[0 : 0.1 : 1]` `m` (значение по умолчанию) | вектор

Положение вала.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On, параметр Advanced Bending Bending vibration analysis method, устанавливается на Eigenmodes и параметр Advanced Bending, Bending mode determination установлен в User defined. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и Усовершенствованные Зависимости от Параметра Изгиба.

`Mode shape matrix` — Матрица формы режима
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0; 0.309, 0, 0, 0.309, 0.5878, 0, 0, 0.5878, 0.809, 0, 0, 0.809, 0.9511, 0, 0, 0.9511; 0.5878, 0, 0, 0.5878, 0.9511, 0, 0, 0.9511, 0.9511, 0, 0, 0.9511, 0.5878, 0, 0, 0.5878; 0.809, 0, 0, 0.809, 0.9511, 0, 0, 0.9511, 0.309, 0, 0, 0.309, -0.5878, 0, 0, -0.5878; 0.9511, 0, 0, 0.9511, 0.5878, 0, 0, 0.5878, -0.5878, 0, 0, -0.5878, -0.9511, 0, 0, -0.9511; 1, 0, 0, 1, 0, 0, 0, 0, -1, 0, 0, -1, 0, 0, 0, 0; 0.9511, 0, 0, 0.9511, -.5878, 0, 0, -0.5878, -0.5878, 0, 0, -0.5878, 0.9511, 0, 0, 0.9511;0.809, 0, 0, 0.809, -.9511, 0, 0, -.9511, 0.309, 0, 0, 0.309, 0.5878, 0, 0, 0.5878; 0.5878, 0, 0, 0.5878, -0.9511, 0, 0, -0.9511, 0.9511, 0, 0, 0.9511, -0.5878, 0, 0, -0.5878; 0.309, 0, 0, 0.309, -0.5878, 0, 0, -0.5878, 0.809, 0, 0, 0.809, -0.9511, 0, 0, -0.9511; 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] (значение по умолчанию) | вектор

Матрица формы режима имеет размерности n-by-2m, где n является длиной элементов в векторе Shaft position, и m является длиной вектора Modal frequencies. Матрица формы режима имеет форму $[U_{1 x} U_{1 y} U_{2 x} U_{2 y} \dots U_{m x} U_{m y}]$ , где вектор-столбцы _Uix и _Uiy являются отклонениями формы режима в x и направлениях y, соответственно, для $i^{t h}$ узел. Алгоритм составляет свойства, заданные для Shaft и параметров Bending, которые используются, чтобы вычислить модальные свойства.

Зависимости

Этот параметр видим только, когда параметр Shaft, Model bending установлен в On, параметр Advanced Bending Bending vibration analysis method, устанавливается на Eigenmodes и параметр Advanced Bending, Bending mode determination установлен в User defined. Для получения дополнительной информации смотрите Зависимости от Параметра Вала и [6].

Начальные условия

`Initial shaft torsional deflection` — Начальный вал крутильное отклонение
`0` `rad` (значение по умолчанию) | неотрицательный скаляр

Угловое отклонение вала в начале симуляции.

Положительное начальное отклонение приводит к положительному вращению основы, B, конца вала относительно последователя, F, конца вала.

`Initial shaft angular velocity` — Начальная угловая скорость
`0` `rpm` (значение по умолчанию) | неотрицательный скаляр

Угловая скорость основы, B, конца вала относительно последователя, F, конца вала в начале симуляции.

Образцовые примеры

Гибкий вал

Два гибких алюминиевых вала смоделировали использование подхода сосредоточенного параметра. Оба вала состоят из 20 сегментов, содержащих инерцию, затухание, и жесткие крутильные пружины. В начале симуляции разблокирована муфта, и управляемый вал свободен. Обратите внимание на то, что начальная скорость вала двигателя установлена в 200 рад/с и что система запускается в устойчивом состоянии. Муфта затрагивает и расцепляет во время теста, и во время каждого события эффект гибкости вала виден в результатах симуляции.

Открытая модель

Shaft with Torsional and Transverse Flexibility

Вал с крутильной и поперечной гибкостью

Два гибких вала, которые имеют крутильную и поперечную гибкость. Один вал вычисляет вычисленный eigenmodes использования поперечного движения, и другой вал использует подход сосредоточенного параметра. Граничные условия на валах могут быть изменены на масках блока.

Открытая модель

Ссылки

[1] Адамс, M.L., вращение вибрации машинного оборудования. КРК-Пресс, Нью-Йорк, 2010.

[2] Купайтесь, K. J. процедуры конечного элемента. Prentice Hall, Inc, Соединенные Штаты, 1996.

[3] Chudnovsky, V., Кеннеди, D, Мукерджи, A. и Wendlandt, J., моделируя гибкие тела в SimMechanics и Simulink. Обзор MATLAB, 14 (3), май 2006,

[4] Миллер, S., Соарес, T., Ван Веддинджен, Y., Wendlandt, J., моделируя гибкие тела с Simscape Multibody. MathWorks, 2017.

[5] Muszynska, A., Rotordynamics, Taylor & Francis, 2005

[6] Рао, судно, вибрация непрерывных систем. John Wiley & Sons, Хобокен, NJ, 2007.

[7] Ву, J.S., Лин, F.T., Шоу, H.J., аналитическое решение для кружения скоростей и форм режима вала распределенной массы с произвольными твердыми дисками. Журнал ASME прикладной механики, объем 81, 2014.

Документация

Гибкий вал

Описание

Крутильная модель

Примечание

Размерности и свойства материала

Внутреннее существенное затухание

Изгиб модели

Подход сосредоточенного параметра

Подход Eigenmodes

Примечание

Улучшите скорость симуляции или точность

Ограничения и предположения

Порты

Вывод

Fr — Обеспечьте при переносе поддержек физический сигнал

M Момент при переносе поддержек физический сигнал

V Вал переводная скорость физический сигнал

W Вал угловая скорость физический сигнал

Сохранение

B Основа вращательное механическое устройство

F Последователь вращательное механическое устройство

Параметры

Вал

Опция модели Model bending — Bending Off (значение по умолчанию) | On

Зависимости

Parameterization — Метод параметризации By stiffness and inertia (значение по умолчанию) | By material properties

Зависимости

Number of segments — Количество сегментов вала 1 (значение по умолчанию) | положительное целое число

Torsional stiffness — Существенная жесткость 2e5 N*m/rad (значение по умолчанию) | положительная скалярная величина

Зависимости

Torsional Inertia — Инерция вала 0.02 kg*m^2 (значение по умолчанию) | положительная скалярная величина

Зависимости

Shaft length — Длина вала 1 m (значение по умолчанию) | положительная скалярная величина

Зависимости

Bending rigidity — Изгиб жесткости 5e5 m^4*Pa (значение по умолчанию) | положительная скалярная величина

Зависимости

Linear density — Линейная плотность 19 kg/m (значение по умолчанию) | положительная скалярная величина

Зависимости

Shaft geometry — Поперечное сечение вала Solid (значение по умолчанию) | Annular

Зависимости

Shaft outer diameter — Наружный диаметр вала 0.075 m (значение по умолчанию) | положительная скалярная величина

Зависимости

Shaft inner diameter — Вал внутренний диаметр 0.05 m (значение по умолчанию) | положительная скалярная величина

Зависимости

Material density — Существенная плотность 7.8e3 kg/m^3 (значение по умолчанию) | положительная скалярная величина

Зависимости

Shear modulus — Сдвиньте модуль 7.93e9 Pa (значение по умолчанию) | положительная скалярная величина

Зависимости

Young's modulus — Модуль молодежи 200e9 Pa (значение по умолчанию) | положительная скалярная величина

Зависимости

Скрученность

Damping ratio from internal losses — Материальное отношение затухания 0.01 (значение по умолчанию) | положительная скалярная величина

Viscous friction coefficients at base (B) and follower (F) — Вязкие коэффициенты трения [0, 0] N*m/(rad/s) (значение по умолчанию) | неотрицательный вектор

Изгиб

Base (B) mounting type — Базовый тип монтирования Clamped (значение по умолчанию) | Pinned | Free | Bearing matrix

Зависимости

Base (B) translational stiffness [x y] — Основывайте переводную жесткость [10e7 10e7] N/m (значение по умолчанию) | неотрицательный вектор

Зависимости

Base (B) rotational stiffness [x y] — Основывайте вращательную жесткость [10e5 10e5] N*m/rad (значение по умолчанию) | неотрицательный вектор

Зависимости

Follower (F) mounting type — Последователь, монтирующий тип Clamped (значение по умолчанию) | Pinned | Free | Bearing matrix

Зависимости

Follower (F) translational stiffness [x y] — Последователь переводная жесткость [10e7 10e7] N/m (значение по умолчанию) | неотрицательный вектор

Зависимости

Follower (F) rotational stiffness [x y] — Последователь вращательная жесткость [10e5 10e5] N*m/rad (значение по умолчанию) | неотрицательный вектор

Зависимости

Damping constant proportional to mass — Ослабляя постоянный, a 10 1/s (значение по умолчанию) | положительная скалярная величина

Зависимости

Translation damping coefficient at base(B) and follower(F) — Коэффициент затухания перевода [0, 0] N/(m/s) (значение по умолчанию) | неотрицательный вектор

Зависимости

Rotation damping coefficient at base(B) and follower(F) — Коэффициент затухания вращения [0, 0] N*m/(rad/s) (значение по умолчанию) | неотрицательный вектор

Зависимости

Damping constant proportional to stiffness — Ослабляя постоянный, b 1e-8 s (значение по умолчанию) | положительная скалярная величина

Зависимости

Rigid masses concentrically attached to shaft — Тип твердых масс присоединяется к валу None (значение по умолчанию) | Point mass | Disk

Зависимости

Зависимости

Rigid masses — Масса твердых масс концентрически присоединяется к валу 2 kg (значение по умолчанию) | неотрицательный скаляр или вектор

Зависимости

`Fr` — Обеспечьте при переносе поддержек
физический сигнал

`M` Момент при переносе поддержек
физический сигнал

`V` Вал переводная скорость
физический сигнал

`W` Вал угловая скорость
физический сигнал

`B` Основа
вращательное механическое устройство

`F` Последователь
вращательное механическое устройство

Опция модели `Model bending` — Bending
`Off` (значение по умолчанию) | `On`

`Parameterization` — Метод параметризации
`By stiffness and inertia` (значение по умолчанию) | `By material properties`

`Number of segments` — Количество сегментов вала
`1` (значение по умолчанию) | положительное целое число

`Torsional stiffness` — Существенная жесткость
`2e5` `N*m/rad` (значение по умолчанию) | положительная скалярная величина

`Torsional Inertia` — Инерция вала
`0.02` `kg*m^2` (значение по умолчанию) | положительная скалярная величина

`Shaft length` — Длина вала
`1` `m` (значение по умолчанию) | положительная скалярная величина

`Bending rigidity` — Изгиб жесткости
`5e5` `m^4*Pa` (значение по умолчанию) | положительная скалярная величина

`Linear density` — Линейная плотность
`19` `kg/m` (значение по умолчанию) | положительная скалярная величина

`Shaft geometry` — Поперечное сечение вала
`Solid` (значение по умолчанию) | `Annular`

`Shaft outer diameter` — Наружный диаметр вала
`0.075` `m` (значение по умолчанию) | положительная скалярная величина

`Shaft inner diameter` — Вал внутренний диаметр
`0.05` `m` (значение по умолчанию) | положительная скалярная величина

`Material density` — Существенная плотность
`7.8e3` `kg/m^3` (значение по умолчанию) | положительная скалярная величина

`Shear modulus` — Сдвиньте модуль
`7.93e9` `Pa` (значение по умолчанию) | положительная скалярная величина

`Young's modulus` — Модуль молодежи
`200e9` `Pa` (значение по умолчанию) | положительная скалярная величина

`Damping ratio from internal losses` — Материальное отношение затухания
`0.01` (значение по умолчанию) | положительная скалярная величина

`Viscous friction coefficients at base (B) and follower (F)` — Вязкие коэффициенты трения
`[0, 0]` `N*m/(rad/s)` (значение по умолчанию) | неотрицательный вектор

`Base (B) mounting type` — Базовый тип монтирования
`Clamped` (значение по умолчанию) | `Pinned` | `Free` | `Bearing matrix`

`Base (B) translational stiffness [x y]` — Основывайте переводную жесткость
`[10e7 10e7]` `N/m` (значение по умолчанию) | неотрицательный вектор

`Base (B) rotational stiffness [x y]` — Основывайте вращательную жесткость
`[10e5 10e5]` `N*m/rad` (значение по умолчанию) | неотрицательный вектор

`Follower (F) mounting type` — Последователь, монтирующий тип
`Clamped` (значение по умолчанию) | `Pinned` | `Free` | `Bearing matrix`

`Follower (F) translational stiffness [x y]` — Последователь переводная жесткость
`[10e7 10e7]` `N/m` (значение по умолчанию) | неотрицательный вектор

`Follower (F) rotational stiffness [x y]` — Последователь вращательная жесткость
`[10e5 10e5]` `N*m/rad` (значение по умолчанию) | неотрицательный вектор

`Damping constant proportional to mass` — Ослабляя постоянный, a
`10` `1/s` (значение по умолчанию) | положительная скалярная величина

`Translation damping coefficient at base(B) and follower(F)` — Коэффициент затухания перевода
`[0, 0]` `N/(m/s)` (значение по умолчанию) | неотрицательный вектор

`Rotation damping coefficient at base(B) and follower(F)` — Коэффициент затухания вращения
`[0, 0]` `N*m/(rad/s)` (значение по умолчанию) | неотрицательный вектор

`Damping constant proportional to stiffness` — Ослабляя постоянный, b
`1e-8` `s` (значение по умолчанию) | положительная скалярная величина

`Rigid masses concentrically attached to shaft` — Тип твердых масс присоединяется к валу
`None` (значение по умолчанию) | `Point mass` | `Disk`

`Rigid masses` — Масса твердых масс концентрически присоединяется к валу
`2` `kg` (значение по умолчанию) | неотрицательный скаляр или вектор

`Rigid mass polar moments of inertia about shaft axis` — Полярные моменты инерции об оси вала
`0.050` `kg*m^2` (значение по умолчанию) | неотрицательный скаляр или вектор

`Static unbalances that excite bending` — Excitational статические дисбалансы
`[.01, .01]` `m*kg` (значение по умолчанию) | неотрицательный вектор

`Static unbalance distances from base (B)` — Статические расстояния дисбаланса от основы
`[.33, .67]` `m` (значение по умолчанию) | неотрицательный вектор

`Static unbalance offset angles` — Статический дисбаланс сместил углы
`[0, pi]` `rad` (значение по умолчанию) | неотрицательный вектор

`Bending vibration analysis method` — Изгиб метода анализа вибрации
`Lumped mass` (значение по умолчанию) | `Eigenmodes`

Метод определения режима `Bending mode determination` — Bending
`Simscape determined` (значение по умолчанию) | `User defined`

`Limit number of modes` — Максимальное количество режимов
`6` (значение по умолчанию) | положительный целочисленный скаляр

`Nominal shaft speed for bending modes` — Номинальная скорость вала для изгиба режимов
`100` `rpm` (значение по умолчанию) | неотрицательный скаляр

`Eigenfrequency initial search resolution` — Разрешение поиска собственной частоты
`5` `rad/s` (значение по умолчанию) | положительный целочисленный скаляр

`Eigenfrequency refine factor` — Фактор улучшения собственной частоты
`1e-4` `rad/s` (значение по умолчанию) | неотрицательный скаляр

`Eigenfrequency upper limit` — Верхний предел собственной частоты
`50000` `rad/s` (значение по умолчанию) | положительный целочисленный скаляр

`Shaft length increments for mode shape computations` — Шаг длины вала
`0.01` `m` (значение по умолчанию) | положительная скалярная величина

`Modal frequencies` — Модальные частоты
`[162, 162, 649, 649, 1460, 1460, 2596, 2596]` `rad/s` (значение по умолчанию) | вектор

`Shaft position` — Положение вала
`[0 : 0.1 : 1]` `m` (значение по умолчанию) | вектор

`Initial shaft torsional deflection` — Начальный вал крутильное отклонение
`0` `rad` (значение по умолчанию) | неотрицательный скаляр

`Initial shaft angular velocity` — Начальная угловая скорость
`0` `rpm` (значение по умолчанию) | неотрицательный скаляр