Специальные темы в БИХ-проекте фильтра

Классический БИХ-проект фильтра

Классический БИХ-метод проектирования фильтра включает следующие шаги.

Найдите аналог lowpass фильтром с частотой среза 1 и переведите этот прототипный фильтр в заданную настройку полосы
Преобразуйте фильтр к цифровой области.
Дискретизируйте фильтр.

Тулбокс обеспечивает функции для каждого из этих шагов.

Разработайте задачу	Доступные функции
Аналог lowpass прототип	`buttap`, `cheb1ap`, `besselap`, `ellipap`, `cheb2ap`
Преобразование частоты	`lp2lp`, `lp2hp`, `lp2bp`, `lp2bs`
Дискретизация	`bilinear`, `impinvar`

Также butter, cheby1, cheb2ord, ellip и функции besself выполняют все шаги проекта фильтра и buttord, cheb1ord, cheb2ord, и функции ellipord обеспечивают вычисление минимального заказа для БИХ-фильтров. Эти функции достаточны для многих проблем проектирования, и более низкие функции уровня обычно не нужны. Но если у вас действительно есть приложение, где необходимо преобразовать ребра полосы аналогового фильтра, или дискретизировать рациональную передаточную функцию, этот раздел описывает инструменты, с которыми можно сделать так.

Аналоговый прототипный проект

Этот тулбокс обеспечивает много функций, чтобы создать lowpass аналоговые прототипные фильтры с частотой среза 1, первый шаг в классическом подходе к БИХ-проекту фильтра.

Приведенная ниже таблица обобщает аналоговые прототипные функции проекта для каждого поддерживаемого типа фильтра; графики для каждого типа показывают в БИХ-Проекте Фильтра.

Отфильтруйте тип	Аналоговая прототипная функция
Функция Бесселя	`[z,p,k] = besselap(n)`
Баттерворт	`[z,p,k] = buttap(n)`
Чебышевский тип I	`[z,p,k] = cheb1ap(n,Rp)`
Чебышевский тип II	`[z,p,k] = cheb2ap(n,Rs)`
Эллиптический	`[z,p,k] = ellipap(n,Rp,Rs)`

Преобразование частоты

Второй шаг в аналоговом методе проектирования прототипирования является преобразованием частоты прототипа lowpass. Тулбокс обеспечивает набор функций, чтобы преобразовать аналог lowpass прототипы (с частотой среза 1 рад/с) в полосу пропускания, highpass, bandstop, и фильтры lowpass с заданной частотой среза.

Преобразование частоты	Функция преобразования
Lowpass к lowpass $s^{'} = s / ω_{0}$	`[numt,dent] = lp2lp (num,den,Wo)` `[At,Bt,Ct,Dt] = lp2lp (A,B,C,D,Wo)`
Lowpass к highpass $s^{'} = \frac{ω_{0}}{s}$	`[numt,dent] = lp2hp (num,den,Wo)` `[At,Bt,Ct,Dt] = lp2hp (A,B,C,D,Wo)`
Lowpass к полосе пропускания $s^{'} = \frac{ω_{0}}{B_{ω}} \frac{{(s / ω_{0})}^{2} + 1}{s / ω_{0}}$	`[numt,dent] = lp2bp (num,den,Wo,Bw)` `[At,Bt,Ct,Dt] = lp2bp (A,B,C,D,Wo,Bw)`
Lowpass к bandstop $s^{'} = \frac{B_{ω}}{ω_{0}} \frac{s / ω_{0}}{{(s / ω_{0})}^{2} + 1}$	`[numt,dent] = lp2bs (num,den,Wo,Bw)` `[At,Bt,Ct,Dt] = lp2bs( A,B,C,D,Wo,Bw)`

Преобразование частоты

Функция преобразования

Lowpass к lowpass

$s^{'} = s / ω_{0}$

[numt,dent] = lp2lp (num,den,Wo)

[At,Bt,Ct,Dt] = lp2lp (A,B,C,D,Wo)

Lowpass к highpass

$s^{'} = \frac{ω_{0}}{s}$

[numt,dent] = lp2hp (num,den,Wo)

[At,Bt,Ct,Dt] = lp2hp (A,B,C,D,Wo)

Lowpass к полосе пропускания

$s^{'} = \frac{ω_{0}}{B_{ω}} \frac{{(s / ω_{0})}^{2} + 1}{s / ω_{0}}$

[numt,dent] = lp2bp (num,den,Wo,Bw)

[At,Bt,Ct,Dt] = lp2bp (A,B,C,D,Wo,Bw)

Lowpass к bandstop

$s^{'} = \frac{B_{ω}}{ω_{0}} \frac{s / ω_{0}}{{(s / ω_{0})}^{2} + 1}$

[numt,dent] = lp2bs (num,den,Wo,Bw)

[At,Bt,Ct,Dt] = lp2bs( A,B,C,D,Wo,Bw)

Как показано все функции преобразования частоты могут принять две модели линейной системы: передаточная функция и форма пространства состояний. Для полосы пропускания и bandstop случаев

$ω_{0} = \sqrt{ω_{1} ω_{2}}$

$B_{ω} = ω_{2} - ω_{1}$

где _ω1 является ребром нижней полосы, и _ω2 является ребром верхней полосы.

Функции преобразования частоты выполняют подстановку переменных частоты. В случае lp2bp и lp2bs, это - замена второго порядка, таким образом, выходной фильтр является дважды порядком входа. Для lp2lp и lp2hp, выходной фильтр является тем же порядком как вход.

Чтобы начать разрабатывать полосу пропускания порядка 10 Чебышевский Тип , который я фильтрую со значением 3 дБ для пульсации полосы пропускания, входят

[z,p,k] = cheb1ap(10,3);

Выходные параметры z, p и k содержат нули, полюса и усиление lowpass аналогового фильтра с частотой среза _Ωc равный 1 рад/с. Используйте функцию, чтобы преобразовать этот прототип lowpass к полосовому аналоговому фильтру с ребрами полосы _Ω1 = π/5 и _Ω2 = π. Во-первых, преобразуйте фильтр в форму пространства состояний, таким образом, функция lp2bp может принять его:

[A,B,C,D] = zp2ss(z,p,k);   % Convert to state-space form.

Теперь, найдите пропускную способность и центральную частоту, и вызовите lp2bp:

u1 = 0.1*2*pi;
u2 = 0.5*2*pi;   % In radians per second
Bw = u2-u1;
Wo = sqrt(u1*u2);
[At,Bt,Ct,Dt] = lp2bp(A,B,C,D,Wo,Bw);

Наконец, вычислите частотную характеристику и постройте ее значение:

[b,a] = ss2tf(At,Bt,Ct,Dt);        % Convert to TF form
w = linspace(0.01,1,500)*2*pi;     % Generate frequency vector
h = freqs(b,a,w);                  % Compute frequency response
semilogy(w/2/pi,abs(h))            % Plot log magnitude vs. freq
xlabel('Frequency (Hz)')
grid

Отфильтруйте дискретизацию

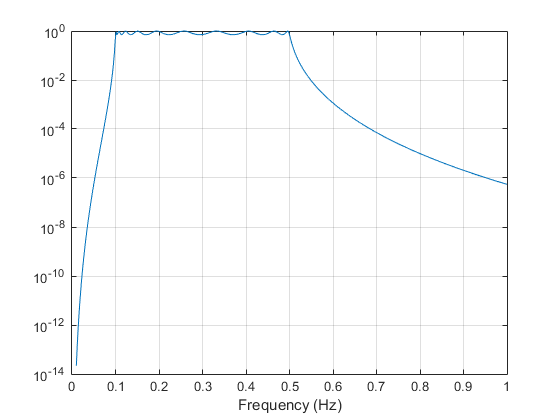
Третий шаг в аналоговом методе прототипирования является преобразованием фильтра к области дискретного времени. Тулбокс предоставляет два метода для этого: импульс инвариантные и билинейные преобразования. Функции проекта фильтра butter, cheby1, cheby2 и ellip используют билинейное преобразование для дискретизации на этом шаге.

Аналого-цифровое преобразование	Функция преобразования
Импульсная инвариантность	`[numd,dend] = impinvar (num,den,fs)`
Билинейное преобразование	`[zd,pd,kd] = bilinear (z,p,k,fs,Fp)` `[numd,dend] = bilinear (num,den,fs,Fp)` `[Ad,Bd,Cd,Dd] = bilinear (At,Bt,Ct,Dt,fs,Fp)`

Аналого-цифровое преобразование

Функция преобразования

Импульсная инвариантность

[numd,dend] = impinvar (num,den,fs)

Билинейное преобразование

[zd,pd,kd] = bilinear (z,p,k,fs,Fp)

[numd,dend] = bilinear (num,den,fs,Fp)

[Ad,Bd,Cd,Dd] = bilinear (At,Bt,Ct,Dt,fs,Fp)

Импульсная инвариантность

impinvar функции тулбокса создает цифровой фильтр, импульсный ответ которого является выборками непрерывного импульсного ответа аналогового фильтра. Эта функция работает только над, просачивается форма передаточной функции. Для лучших результатов аналоговый фильтр должен иметь незначительное содержимое частоты выше половины частоты дискретизации, потому что такое высокочастотное содержимое искажается в нижние полосы после выборки. Импульсная инвариантность работает на некоторый lowpass и полосовые фильтры, но не подходит для highpass и заграждающих фильтров.

Разработайте Чебышевский Тип, я фильтрую и строю его частоту и фазовый отклик с помощью FVTool:

[bz,az] = impinvar(b,a,2);
fvtool(bz,az)

Нажмите кнопку на панели инструментов Magnitude and Phase Response.

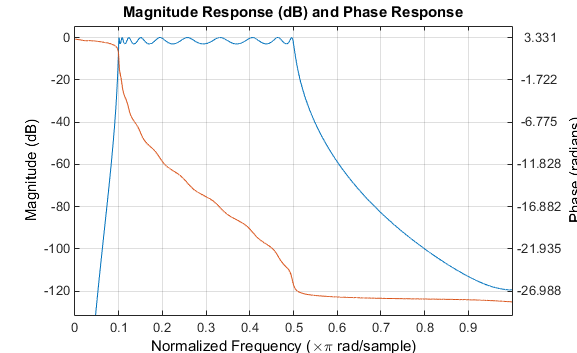
Импульсная инвариантность сохраняет частоты среза 0,1 Гц и 0,5 Гц.

Билинейное преобразование

Билинейное преобразование является нелинейным отображением непрерывной области к дискретной области; это сопоставляет s - плоскость в z - плоскость

$H (z) = H (s) |_{s = k \frac{z - 1}{z + 1}}$

Билинейное преобразование сопоставляет the jΩ-axis непрерывной области к модульному кругу дискретной области согласно

$ω = 2 {загар}^{- 1} (\frac{Ω}{k})$

bilinear функции тулбокса реализует эту операцию, где частота, деформирующая постоянный k, равна дважды частоте дискретизации (2*fs) по умолчанию и равна $2 π f_{p} / загар (π f_{p} / f_{s})$ если вы даете bilinear запаздывающий аргумент, который представляет частоту “соответствия” Fp. Если частота соответствия, Fp (в герц) присутствует, bilinear, сопоставляет частоту Ω = 2_πfp (в rad/s) к той же частоте в дискретной области, нормированной к уровню выборки: ω = _2πfp/_fs (в раде/выборке).

Функция bilinear может выполнить это преобразование на трех различных представлениях линейной системы: нули и полюса, передаточная функция и форма пространства состояний. Попытайтесь вызвать bilinear с матрицами пространства состояний, которые описывают Чебышевский Тип, который я фильтрую от предыдущего раздела, с помощью частоты дискретизации 2 Гц, и сохраняя ребро нижней полосы 0,1 Гц:

[Ad,Bd,Cd,Dd] = bilinear(At,Bt,Ct,Dt,2,0.1);

Частотная характеристика получившегося цифрового фильтра

[bz,az] = ss2tf(Ad,Bd,Cd,Dd);       % Convert to TF
fvtool(bz,az)

Нажмите кнопку на панели инструментов Magnitude and Phase Response.

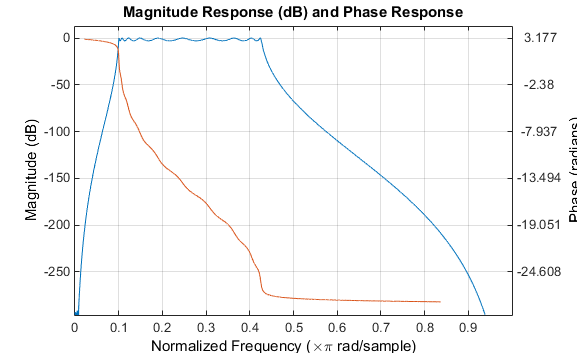
Ребро нижней полосы на уровне 0,1 Гц как ожидалось. Заметьте, однако, что ребро верхней полосы - немного меньше чем 0,5 Гц, несмотря на то, что в аналоговой области это были точно 0,5 Гц. Это иллюстрирует нелинейную природу билинейного преобразования. Чтобы противодействовать этой нелинейности, необходимо создать аналоговые доменные фильтры с “предварительно деформированными” ребрами полосы, которые сопоставляют с правильными местоположениями после билинейного преобразования. Здесь предварительно деформированные частоты u1 и u2 генерируют Bw и Wo для функции lp2bp:

fs = 2;                           % Sampling frequency (hertz)
u1 = 2*fs*tan(0.1*(2*pi/fs)/2);   % Lower band edge (rad/s)
u2 = 2*fs*tan(0.5*(2*pi/fs)/2);   % Upper band edge (rad/s)
Bw = u2 - u1;                     % Bandwidth
Wo = sqrt(u1*u2);                 % Center frequency
[At,Bt,Ct,Dt] = lp2bp(A,B,C,D,Wo,Bw);

Цифровой полосовой фильтр с правильными ребрами полосы 0.1 и 0.5 раза частота Найквиста

[Ad,Bd,Cd,Dd] = bilinear(At,Bt,Ct,Dt,fs);

Полосовые фильтры в качестве примера от последних двух разделов могли также быть созданы в одном операторе с помощью полной БИХ-функции проекта cheby1. Например, аналоговая версия примера Чебышевский фильтр

[b,a] = cheby1(5,3,[0.1 0.5]*2*pi,'s');

Обратите внимание на то, что ребра полосы находятся в rad/s для аналоговых фильтров, тогда как для цифрового случая, частота нормирована:

[bz,az] = cheby1(5,3,[0.1 0.5]);

Все полные функции проекта вызывают bilinear внутренне. Они предварительно деформируют ребра полосы по мере необходимости, чтобы получить правильный цифровой фильтр.

Документация