besselYФункции Бесселя второго вида
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
besselY(v, z)
besselJ(v, z) представляет Функции Бесселя второго вида:
 .
.
Здесь J ν (z) являются Функции Бесселя первого вида:
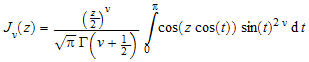 .
.
Функции Бесселя заданы для сложных аргументов v и z.
Значение с плавающей точкой возвращено, если любой из аргументов является числом с плавающей запятой, и другой аргумент является числовым. Для большинства точных аргументов Функции Бесселя возвращают неоцененный вызов функции. Реализованы специальные значения в индексе v = 0 и/или аргумент z = 0. Явные символьные выражения возвращены, когда индекс v является половиной целого числа. Смотрите Пример 2.
Для неотрицательных целочисленных индексов v некоторые Функции Бесселя имеют разрез вдоль отрицательной вещественной оси. Скачок происходит при пересечении этого сокращения. Смотрите Пример 3.
Когда названо аргументами с плавающей точкой, эти функции чувствительны к переменной окружения DIGITS, который определяет числовую рабочую точность.
На неоцененные звонки отвечают для точных или символьных аргументов:
besselY(2, 1 + I), besselY(0, x), besselY(v, x)
![]()
Значения с плавающей точкой возвращены для аргументов с плавающей точкой:
besselY(2, 5.0), besselY(3.2 + I, 10000.0)
![]()
Функции Бесселя могут быть выражены с точки зрения элементарных функций, если индекс является нечетным целочисленным кратным![]() :
:
besselY(1/2, x), besselY(3/2, x)

besselY(5/2, x), besselY(-5/2, x)

Отрицательная вещественная ось является разрезом Функций Бесселя для индексов нецелого числа v. Скачок происходит при пересечении этого сокращения:
besselY(-3/4, -1.2), besselY(-3/4, -1.2 + I/10^10), besselY(-3/4, -1.2 - I/10^10)
![]()
Функции diff, float, limit и series обрабатывают выражения, включающие Функции Бесселя:
diff(besselY(0, x), x, x), float(ln(3 + besselY(17, sqrt(PI))))
![]()
limit(besselY(2, x^2 + 1)*sqrt(x), x = infinity)
![]()
series(besselY(3, x), x = infinity, 3)

|
Арифметическое выражение.
z
Функции Бесселя являются регулярными (голоморфными) функциями z в z - плоское сокращение вдоль отрицательной вещественной оси, и для фиксированного z ≠ 0, каждый - целая (интегральная) функция v.
J v (z) и Y v (z) удовлетворяет уравнению функции Бесселя в w (v, z):
![]() .
.
Когда индексом, v является целым числом, Функциями Бесселя второго вида, управляют отражательные формулы:
![]() .
.