ChiГиперболическая функция интегрального косинуса
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Chi(x)
Chi(x) представляет гиперболический интегральный косинус .
Если x является числом с плавающей запятой, то Chi(x) возвращает результаты с плавающей точкой. Специальные значения Chi(∞) = ∞, Chi(-∞) = ∞ + iπ, Chi(i∞) = iπ/2 и Chi(-i∞) = -iπ/2 реализованы. Поскольку все другие аргументы Chi возвращают символьные вызовы функции.
Когда названо аргументом с плавающей точкой, функции чувствительны к переменной окружения DIGITS, который определяет числовую рабочую точность.
Большинство вызовов с точными аргументами возвращает себя неоцененный:
Chi(1), Chi(sqrt(2)), Chi(x + 1), Chi(I*infinity), Chi(-I*infinity)
![]()
Чтобы аппроксимировать точные результаты с числами с плавающей запятой, используйте float:
float(Chi(1)), float(Chi(sqrt(2)))
![]()
Также используйте значение с плавающей точкой в качестве аргумента:
Chi(1.0), Chi(2.0 + 10.0*I)
![]()
Chi сингулярен в начале координат:
Chi(0)
Error: Singularity. [Chi]
Отрицательная вещественная ось является разрезом Chi. Скачок высоты 2 π i происходит при пересечении этого сокращения:
Chi(-1.0), Chi(-1.0 + 10^(-10)*I), Chi(-1.0 - 10^(-10)*I)
![]()
diff, float, series и другие функции обрабатывают выражения, включающие Chi:
diff(Chi(x), x, x, x), float(ln(3 + Chi(sqrt(PI))))
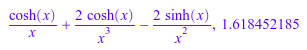
series(Chi(x), x = 0)
![]()
series(Chi(x), x = infinity, 3);
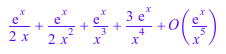
|
Арифметическое выражение.
x
Функции Ci(x)-ln(x) и Chi(x)-ln(x) являются целыми функциями. Таким образом Ci и Chi имеют логарифмическую особенность в начале координат и разрезе вдоль отрицательной вещественной оси. Значения на отрицательной вещественной оси совпадают с пределом “сверху”:
![]()
для действительного x <0.
Ci и Chi связаны Ci (x) - ln (x) = Chi (i x) - ln (i x) для всего x в комплексной плоскости.
[1] Abramowitz, M. и я. Stegun, “Руководство математических функций”, Dover Publications Inc., Нью-Йорк (1965).