Документация

Типы чисел

Используя MuPAD^®, можно работать со следующими типами чисел:

По умолчанию MuPAD принимает, что все переменные являются комплексными числами.

Вычислите с Integers и Rationals

При вычислении с целыми числами и рациональными числами, MuPAD возвращает целочисленные результаты

2 + 2

или рациональные результаты:

(1 + (5/2*3))/(1/7 + 7/9)^2

Если MuPAD не может найти представление выражения в целочисленной или рациональной форме, он возвращает символьное выражение:

56^(1/2)

Вычислите со специальными математическими константами

Можно выполнить точные вычисления, которые включают константы =exp(1)=2.718... и π=3.1415...:

2*(exp(2)/PI)

Для получения дополнительной информации о математических константах, реализованных в MuPAD, смотрите Константы.

Аппроксимируйте численно

По умолчанию MuPAD выполняет все вычисления в точной форме. Чтобы получить приближение с плавающей точкой к выражению, используйте команду float. Например:

float(sqrt(56))

Точность приближения зависит от значения глобальной переменной DIGITS. Переменная DIGITS может принять любое целочисленное значение между 1 и ²²⁹ + 1. Например:

DIGITS:=20: float(sqrt(56))

Значение по умолчанию переменной DIGITS равняется 10. Восстановить значение по умолчанию, введите:

delete DIGITS

Когда MuPAD выполняет арифметические операции на числах, включающих по крайней мере одно число с плавающей запятой, он автоматически переключается, чтобы аппроксимировать числовые вычисления:

(1.0 + (5/2*3))/(1/7 + 7/9)^2

Если выражение включает точные значения такой как или sin (2) и числа с плавающей запятой, MuPAD аппроксимирует только числа:

1.0/3*exp(1)*sin(2)

Чтобы аппроксимировать выражение с точными значениями, используйте команду float:

float(1.0/3*exp(1)*sin(2))

или используйте числа с плавающей запятой в качестве аргументов:

1.0/3*exp(1.0)*sin(2.0)

Также можно аппроксимировать константы π и:

DIGITS:=30: float(PI); float(E); delete DIGITS

Работа с комплексными числами

Во входных областях MuPAD распознает верхний регистр I мнимой единицей. В выходных областях MuPAD использует нижний регистр i, чтобы отобразить мнимую единицу:

sqrt(-1), I^2

И действительные и мнимые части комплексного числа могут содержать целые числа, rationals, и числа с плавающей запятой:

(1 + 0.2*I)*(1/2 + I)*(0.1 + I/2)^3

Если вы используете точные выражения, например, MuPAD не всегда возвращает результат в Декартовых координатах:

1/(sqrt(2) + I)

Чтобы разделить результат в его действительные и мнимые части, используйте команду rectform:

rectform(1/(sqrt(2) + I))

Функции Re и Im возвращают действительные и мнимые части комплексного числа:

Re(1/(2^(1/2) + I))

Im(1/(2^(1/2) + I))

Функциональный conjugate возвращает сопряженное комплексное число:

conjugate(1/(2^(1/2) + I))

Функциональный abs и arg возвращают абсолютное значение и угол в полярных координатах комплексного числа:

abs(1/(2^(1/2) + I));
arg(1/(2^(1/2) + I))

Производные Одно Переменных выражений

Чтобы вычислить производную математического выражения, используйте команду diff. Например:

f := 4*x + 6*x^2 + 4*x^3 + x^4: diff(f, x)

Частные производные

Также можно вычислить частную производную многомерного выражения:

f := y^2 + 4*x + 6*x^2 + 4*x^3 + x^4: diff(f, y)

Второй - и производные высшего порядка

Чтобы найти производные высшего порядка, используйте вложенный вызов команды diff

diff(diff(diff(sin(x), x), x), x)

или, более эффективно:

diff(sin(x), x, x, x)

Можно использовать оператор последовательности $, чтобы вычислить производные второго или высшего порядка:

diff(sin(x), x $ 3)

Смешанные производные

diff(f, x1, x2, ...) эквивалентен diff(...diff(diff(f, x1), x2)...). Система сначала дифференцирует f относительно x1, и затем дифференцирует результат относительно x2 и так далее. Например,

diff(diff((x^2*y^2 + 4*x^2*y + 6*x*y^2), y), x)

эквивалентно

diff(x^2*y^2 + 4*x^2*y + 6*x*y^2, y, x)

Это предположение достаточно для большинства технических и научных проблем.

Для дальнейших вычислений удалите f:

delete f:

Производные функции

MuPAD обеспечивает две функции дифференцирования, diff и D. Функция diff служит для дифференциации математических выражений, таких как sin(x), cos(2y), exp(x^2), x^2 + 1, f(y), и так далее.

Чтобы дифференцировать стандартную функцию, такую как sin, exp, heaviside, или пользовательская функция, такая как f:= x -> x^2 + 1, использует дифференциальный оператор D:

D(sin), D(exp), D(heaviside)

f := x -> x^2 + 1: D(f)

' является ярлыком для дифференциального оператора D:

sin', sin'(x), f'

D(f)(x) команды принимает, что f является одномерной функцией и представляет производную f в точке x. Например, производная синусоидальной функции при точке x ²:

D(sin)(x^2)

Обратите внимание на то, что в этом примере вы дифференцируете функцию sin, не функциональный f := x -> sin(x^2). Дифференциация f возвращает этот результат:

f := x -> sin(x^2): D(f)

Для получения дополнительной информации об использовании оператора D для вычисления второго - и производные высшего порядка функций, смотрите Дифференцирующиеся Функции.

Неопределенные интегралы

Чтобы вычислить интегралы используют команду int. Например, можно вычислить неопределенные интегралы:

int((cos(x))^3, x)

Команда int возвращает результаты без постоянного интегрирования.

Определенные интегралы

Чтобы найти определенный интеграл, передайте верхнее и нижние пределы интервала интегрирования к функции int:

int((cos(x))^3, x = 0..PI/4)

Можно использовать бесконечность в качестве предела при вычислении определенного интеграла:

int(sin(x)/x, x = -infinity..infinity)

Числовое приближение

Если MuPAD не может выполнить выражение в закрытой форме, он возвращает выражение. Например:

int(sin(x^2)^2, x = -1..1)

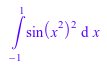
Можно аппроксимировать значение интеграла численно с помощью команды float. Например:

float(int(sin(x^2)^2,(x = -1..1)))

Также можно использовать команду numeric::int, чтобы оценить интеграл численно. Например:

numeric::int(sin(x^2)^2, x = -1..1)

Создайте матрицу

Чтобы создать матрицу в MuPAD, используйте команду matrix:

A := matrix([[1, 2], [3, 4], [5, 6]]);
B := matrix([[1, 2, 3], [4, 5, 6]])

Также можно создать векторы с помощью команды matrix:

V := matrix([1, 2, 3])

Можно явным образом объявить матричные размерности:

C := matrix(3, 3, [[-1, -2, -3], [-4, -5, -6], [-7, -8, -9]]);
W := matrix(1, 3, [1, 2, 3])

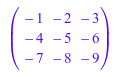
Если вы объявляете матричные размерности и вводите строки или столбцы короче, чем заявленные размерности, MuPAD заполняет матрицу нулевыми элементами:

F := matrix(3, 3, [[1, -1, 0], [2, -2]])

Если вы объявляете матричные размерности и вводите строки или столбцы дольше, чем заявленные размерности, MuPAD возвращает следующее сообщение об ошибке:

matrix(3, 2, [[-1, -2, -3], [-4, -5, -6], [-7, -8, -9]])

Error: Number of columns does not match. [(Dom::Matrix(Dom::ExpressionField()))::mkSparse]

Также можно создать диагональную матрицу:

G := matrix(4, 4, [1, 2, 3, 4], Diagonal)

Работайте с матрицами

Чтобы добавить, вычтите, умножьте и разделите матрицы, используйте типичные арифметические операторы. Например, чтобы умножить две матрицы, введите:

A := matrix([[1, 2], [3, 4], [5, 6]]);
B := matrix([[1, 2, 3], [4, 5, 6]]);
A*B

Если вы добавляете номер x в матричный A, MuPAD добавляет времена x единичная матрица в A. Например:

C := matrix(3, 3, [[-1, -2, -3], [-4, -5, -6], [-7, -8, -9]]);
C + 10

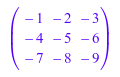
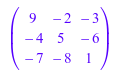
Можно вычислить детерминант и инверсию квадратной матрицы:

G := matrix([[1, 2, 0], [2, 1, 2], [0, 2, 1]]); det(G); 1/G

Библиотека линейной алгебры

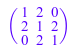
Библиотека MuPAD linalg содержит функции для обработки линейных алгебраических операций. Пользуясь этой библиотекой, можно выполнить большое разнообразие вычислений на матрицах и векторах. Например, чтобы найти собственные значения квадратных матриц G, F, и (A*B), используют linalg:: команда собственного значения:

linalg::eigenvalues(G);
linalg::eigenvalues(F);
linalg::eigenvalues(A*B)

Чтобы видеть все функции, доступные в этой библиотеке, введите info(linalg) во входную область. Можно получить подробную информацию об определенной функции путем ввода ?functionname. Например, чтобы открыть страницу справки на функции собственного значения, введите ?linalg::eigenvalues.

Решите уравнения с одной переменной

Чтобы решить простое алгебраическое уравнение с одной переменной, используйте команду solve:

solve(x^5 + 3*x^4 - 23*x^3 - 51*x^2 + 94*x + 120 = 0, x)

Решение уравнений с параметрами

Можно решить уравнение с символьными параметрами:

solve(a*x^2 + b*x + c = 0, x)

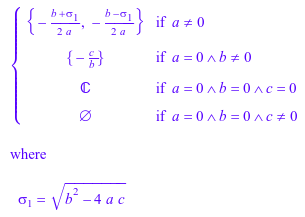
Если вы хотите получить решение для особых значений параметров, используйте команду assuming. Например, можно решить следующее уравнение, принимающее, что a положителен:

solve(a*x^2 + b*x + c = 0, x) assuming a > 0

Для получения дополнительной информации смотрите Используя Предположения.

Решите системы уравнений

Можно решить систему уравнений:

solve([x^2 + x*y + y^2 = 1, x^2 - y^2 = 0], [x, y])

или можно решить систему уравнений, содержащую символьные параметры:

solve([x^2 + y^2 = a, x^2 - y^2 = b], [x, y])

Решите Обыкновенные дифференциальные уравнения

Можно решить различные типы обыкновенных дифференциальных уравнений:

o := ode(x^2*diff(y(x), x, x) + 2*x*diff(y(x), x) + x, y(x)):
solve(o)

Решите неравенства

Кроме того, можно решить неравенства:

solve(x^4 >= 5, x)

Если вы хотите получить результат по полю вещественных чисел только, assume, что x является вещественным числом:

assume(x in R_); solve(x^4 >= 5, x)

Можно выбрать решения, которые положительны:

solve(x^4 >= 5, x) assuming x > 0

Преобразуйте и упростите многочленные выражения

Существует несколько способов представить многочленное выражение. Стандартная полиномиальная форма является суммой одночленов. Чтобы получить эту форму многочленного выражения, используйте команду expand:

expand((x - 1)*(x + 1)*(x^2 + x + 1)*
(x^2 + 1)*(x^2 - x + 1)*(x^4 - x^2 + 1))

Можно учесть это выражение с помощью команды factor:

factor(x^12 - 1)

Для многомерных выражений можно задать переменную и собрать условия с теми же степенями в этой переменной:

collect((x - a)^4 + a*x^3 + b^2*x + b*x + 10*a^4 +
(b + a*x)^2, x)

Для рациональных выражений можно использовать команду partfrac, чтобы представить выражение как сумму частей (разложение элементарной дроби). Например:

partfrac((7*x^2 + 7*x + 6)/(x^3 + 2*x^2 + 2*x + 1))

MuPAD также обеспечивает две общих функции упрощения: simplify и Simplify. Функция simplify быстрее, и она может обработать большинство элементарных выражений:

simplify((x - 1)*(x + 1)*(x^2 + x + 1)*(x^2 + 1)*
(x^2 - x + 1)*(x^4 - x^2 + 1))

Функция Simplify ищет более простые результаты глубже, чем функция simplify. Более обширный поиск делает эту функцию медленнее, чем simplify. Функция Simplify позволяет вам расширять набор правила упрощения со своими собственными правилами и служит лучше для преобразования более сложных выражений. Для элементарных выражений это дает тот же результат как упростите:

Simplify((x - 1)*(x + 1)*(x^2 + x + 1)*(x^2 + 1)*
(x^2 - x + 1)*(x^4 - x^2 + 1))

Для следующего выражения две функции упрощения дают различные формы того же математического выражения:

f := exp(wrightOmega(-ln(3/5)))*exp(ln(5) - ln(3)):
simplify(f);
Simplify(f)

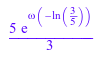
Обратите внимание на то, что нет никакой универсальной стратегии упрощения, потому что значение самого простого представления символьного выражения не может быть задано ясно. Различные проблемы требуют различных форм того же математического выражения. Можно использовать общие функции упрощения simplify и Simplify, чтобы проверять, дают ли они более простую форму выражения, вы используете.

Преобразуйте и упростите тригонометрические выражения

Также можно преобразовать и упростить тригонометрические выражения. Функции для управления тригонометрическими выражениями эквивалентны для многочленных выражений. Например, чтобы расширить тригонометрическое выражение, используйте команду expand:

expand(sin(5*x))

Чтобы учесть тригонометрическое выражение, используйте команду factor:

factor(cos(x)^4 + 4*cos(x)^3*sin(x) + 6*cos(x)^2*sin(x)^2 +
4*cos(x)*sin(x)^3 + sin(x)^4)

Можно использовать общие функции упрощения по тригонометрическим выражениям:

simplify(cos(x)^2 + sin(x)^2)

simplify(cos(x)^4 + sin(x)^4 + sin(x)*cos(x))

Simplify(cos(x)^4 + sin(x)^4 + sin(x)*cos(x))

Решите выражения с предположениями

По умолчанию все переменные в MuPAD представляют комплексные числа. При решении уравнений или упрощении выражений, программное обеспечение рассматривает все возможные случаи для комплексных чисел. Если вы решаете уравнение или упрощаете выражение, это предположение по умолчанию приводит к точному и полному набору результатов включая сложные решения:

solve(x^(5/2) = 1, x)

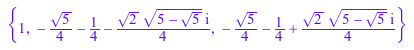
Чтобы получить действительные решения только, передайте предположение MuPAD с помощью команды assuming:

solve(x^(5/2) = 1, x) assuming x in R_

Можно сделать различные предположения на значениях, что переменная представляет. Например, можно решить уравнение, принимающее, что переменная x представляет только положительные значения:

solve(x^4 - 1 = 0, x) assuming x > 0

Можно сделать несколько предположений:

solve(x^4 - a = 0, x) assuming a = 16 and x in R_

Объединяйтесь с предположениями

Можно использовать предположения при интеграции математических выражений. Например, без предположения на переменной x, следующий интеграл зависит от знака выражения x ² - 1:

int(1/abs(x^2 - 1), x)

Если вы знаете, что x> 1, можно передать предположение интегралу:

int(1/abs(x^2 - 1), x) assuming x > 1

Упростите выражения с предположениями

Используя предположения наряду с упрощением функции сужают возможные значения, которые переменные представляют и могут обеспечить намного более короткие результаты, чем одни только функции упрощения. Например:

simplify(sqrt(x^2 + 2*x + 1) + sqrt(x^2 - 2*x + 1) +
sqrt(x^2 + 4*x + 4) + sqrt(x^2 - 4*x + 4))

от

simplify(sqrt(x^2 + 2*x + 1) + sqrt(x^2 - 2*x + 1) +
sqrt(x^2 + 4*x + 4) + sqrt(x^2 - 4*x + 4)) assuming x > 2

Можно передать предположения следующим функциям: expand, simplify, limit, solve и int. Функция Simplify не позволяет предположения на переменных.