combineОбъедините условия той же алгебраической структуры
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
combine(f, <IgnoreAnalyticConstraints>) combine(f,target, <IgnoreAnalyticConstraints>) combine(f,[target1, target2, …], <IgnoreAnalyticConstraints>)
combine(f) переписывает продукты степеней в выражении f как одна степень.
combine(f, target) комбинирует несколько вызовов целевой функции (функций) в выражении f к одному вызову.
combine(f) применяет эти правила перезаписи к продуктам степеней, происходящих как подвыражения в арифметическом expression f:
![]() ,
,
![]() ,
,
![]() .
.
Последние два правила только допустимы в условиях определенных дополнительных ограничений, такой как тогда, когда b является целым числом. За исключением третьего правила, это поведение combine является обратной функциональностью expand. Смотрите Пример 1.
В определенных случаях MuPAD® внутренний simplifier автоматически применяет эти правила в обратном направлении, и combine иногда не имеет никакого эффекта. Смотрите Пример 2.
combine(f, target) применяет правила перезаписи, применимые к целевой функции (функциям) к арифметическому выражению f. Некоторые правила только допустимы в условиях определенных дополнительных ограничений. Для большинства правил combine реализует обратную функциональность expand. Этот список показывает правила перезаписи для целей.
target = arctan:
![]()
для-1 <x <1 и-1 <y <1 .
target = exp (см. пример 4):
![]() ,
,
![]() ,
,
где допустимый, реагируя на свойства.
target = int (см. пример 5):
target = gamma (см. пример 6):
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
 ,
,
для положительных целых чисел n.
target = ln (см. пример 7):
![]() ,
,
![]() ,
,
если b является меньше, чем N. По умолчанию, N = 1000. Можно изменить номер N с помощью команды Pref::autoExpansionLimit. Смотрите Пример 8.
Правила не содержат для произвольных комплексных чисел a, b. Задайте соответствующие свойства для a или b, чтобы включить эти правила перезаписи. Эти правила только применяются к натуральным логарифмам.
target = sincos (см. пример 3):
![]() ,
,
где подобные правила применяются к sin (x) cos (y) и cos (x) cos (y):
![]() .
.
target = sinhcosh:
![]() ,
,
где подобные правила применяются к sinh (x) cosh (y) и cosh (x) cosh (y).
Эти правила применяются рекурсивно к степеням sinh и cosh с положительными интегральными экспонентами.
combine работает рекурсивно над подвыражениями f.
Если второй аргумент является списком целей, то combine применяется к f впоследствии для каждой из целей в списке. Смотрите Пример 10.
Если f является массивом, списком или набором, combine применяется ко всем записям f. Смотрите Пример 11. Если f является полиномом или последовательным расширением типа Series::Puiseux или Series::gseries, combine применяется к каждому коэффициенту. Смотрите Пример 12.
combine реагирует на свойства идентификаторов, появляющихся во входе.
Объедините степени той же основы с помощью combine.
combine(sin(x) + x*y*x^(exp(1)))
![]()
combine также комбинирует степени с той же экспонентой в определенных случаях:
combine(sqrt(2)*sqrt(3))
![]()
В большинстве случаев, однако, combine не комбинирует степени с той же экспонентой:
combine(y^5*x^5)
![]()
Перепишите продукты синусов и косинусов как сумма синусов и косинусов путем установки второго аргумента на sincos:
combine(sin(a)*cos(b) + sin(b)^2, sincos)
![]()
Перепишите суммы синусов и косинусов путем установки второго аргумента на sincos:
combine(cos(a) + sin(a), sincos)
![]()
Полномочия синусов или косинусов с отрицательными целочисленными экспонентами не переписаны:
combine(sin(b)^(-2), sincos)
![]()
Объедините условия с показательной функцией путем определения второго аргумента как exp.
combine(exp(3)*exp(2), exp)
![]()
combine(exp(a)^2, exp)
![]()
Перепишите интегралы путем установки второго аргумента на int.
combine(int(f(x),x)+int(g(x),x),int)
![]()
combine комбинирует постоянный термин с интегралом.
combine(a*int(f(x),x),int)
![]()
combine комбинирует интегралы с теми же пределами.
combine(int(f(x),x=a..b)+int(g(y),y=a..b),int)
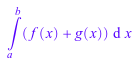
Объедините вызовы gamma путем определения цели как gamma. Функция combine упрощает частных гамм к рациональным выражениям.
combine(gamma(n+3)*gamma(n+4/3) / gamma(n+1) / gamma(n+10/3), gamma)

Этот пример показывает приложение правил для логарифма и их зависимость от свойств идентификаторов, появляющихся во входе. В комплексной плоскости логарифм продукта не всегда равняется сумме логарифмов ее факторов. Для действительных положительных чисел, однако, может применяться это правило.
Попытайтесь объединить условия с вызовами ln путем определения цели как ln.
combine(ln(a) + ln(b), ln)
![]()
combine не комбинирует условия. Установите соответствующие предположения комбинировать условия.
assume(a > 0): assume(b > 0): combine(ln(a) + ln(b), ln)
![]()
unassume(a): unassume(b):
Если a и b являются целыми или рациональными числами, и b является меньше, чем 1000, combine возвращает логарифмы.
combine(3*ln(2), ln)
![]()
Если b больше, чем или равен 1000, combine возвращает результаты как![]() :
:
combine(1234*ln(5), ln)
![]()
Можно изменить предел на номере b при помощи функции Pref::autoExpansionLimit. Например, когда вы используете значение по умолчанию N = 1000, combine возвращает следующий результат для этого логарифма:
combine(12*ln(12), ln)
![]()
Если вы устанавливаете значение Pref::autoExpansionLimit к 10, combine возвращает этот логарифм в своей исходной форме:
Pref::autoExpansionLimit(10): combine(12*ln(12), ln)
![]()
Для дальнейших вычислений восстановите значение по умолчанию Pref::autoExpansionLimit:
Pref::autoExpansionLimit(NIL):
Опция IgnoreAnalyticConstraints применяет набор чисто алгебраических упрощений включая равенство суммы логарифмов и логарифма продукта. Используя опцию IgnoreAnalyticConstraints, вы получаете более простой результат, но тот, который может быть неправильным для некоторых значений a.
Объедините логарифмы с помощью опции IgnoreAnalyticConstraints.
combine(ln(a^5) - ln(a^4), ln, IgnoreAnalyticConstraints)
![]()
Не используя эту опцию, вы получаете математически правильный, но длинный результат:
combine(ln(a^5) - ln(a^4), ln)
![]()
Второй аргумент также может быть списком целей. Затем правила перезаписи для каждой из целей в списке применяются.
Перепишите ln и условия sincos в выражении.
combine(ln(2) + ln(3) + sin(a)*cos(a), [ln, sincos])
![]()
combine сопоставляет с наборами:
combine({sqrt(2)*sqrt(5), sqrt(2)*sqrt(11)})![]()
combine сопоставляет с коэффициентами полиномов:
combine(poly(sin(x)*cos(x)*y, [y]), sincos)
![]()
Однако это не касается indeterminates полинома:
combine(poly(sin(x)*cos(x)), sincos)
![]()
| |
|
Один из идентификаторов: |
|
Примените чисто алгебраические упрощения в выражении. Для получения дополнительной информации см. опции для команды |
Объект того же типа как входной объект f.
f
Опытные пользователи могут расширить функциональность combine путем реализации дополнительных правил перезаписи для других целевых функций. Чтобы расширить функциональность, задайте новый слот target combine. Чтобы задать новый слот, необходимо сначала оставить без защиты идентификатор, который оставляет без защиты использование combine. Впоследствии, команда combine(f, target) приводит к вызову combine::target(f) соответствующей стандартной программы слота.
По умолчанию combine обрабатывает подвыражение g(x1,x2,...) f путем вызова себя рекурсивно для операндов x1, x2, и т.д. Пользователи могут изменить это поведение для своей собственной математической функции, данной функцией environment g путем реализации слота combine g. Чтобы обработать подвыражение g(x1,x2,...), combine затем вызывает стандартную программу слота g::combine с последовательностью аргумента x1,x2,... g.