!!, fact2Двойная функция факториала
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
n !!
fact2(n)
fact2(n) представляет двойной факториал целого числа. Двойной факториал задан
что касается даже положительных целых чисел и
для нечетных положительных целых чисел.
Вызов стенографии n!! эквивалентен fact2(n).
0!! и (-1)!! оба возвращают 1.
Если n является целым числом, больше или равным -1 и меньшим, чем значение, данное Pref::autoExpansionLimit (), то целое число возвращено. Если n является целым числом, меньшим, чем -1 или численное значение нецелого числа затем, ошибка происходит. Если n является символьным выражением, то на символьный звонок fact2 отвечают.
Используйте expand(n!!), чтобы вычислить явный результат для больших целых чисел n, равный или больше, чем Pref::autoExpansionLimit ().
Выражения, включающие символьные вызовы fact2, могут быть переписаны с точки зрения функции gamma rewrite(expression, gamma). Cf. Пример 2.
Обратите внимание на то, что двойной факториальный n!! не равняется выполненному с помощью итераций факториальному (n!)!.
Целые числа производятся, если аргумент является целым числом, больше, чем или равный - 1:
fact2(-1), fact2(0), fact2(5), fact2(16)
На символьный звонок отвечают, если аргумент является символьным выражением:
fact2(n), fact2(4.7*I*n)
Вызовы fact2(n) и n!! эквивалентны:
5!! = fact2(5), fact2(n^2 + 3)
Функциональный rewrite может использоваться, чтобы переписать выражения, включающие fact2 с точки зрения функции gamma. В большинстве случаев Simplify должен использоваться, чтобы получить простой результат:
rewrite(n!!, gamma)
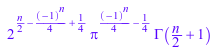
rewrite(fact2(2*n)/fact2(2*n - 1), gamma)
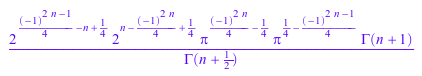
assume(n, Type::Integer): Simplify(%2)
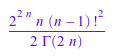
Для эффективности двойной факториал должен быть переписан с точки зрения gamma, если оценка с плавающей точкой для больших аргументов желаема. Следующий вызов производит огромное точное целое число, которое наконец преобразовано в плавание:
float(fact2(2^17))
Следующий вызов намного быстрее, потому что никакой точный промежуточный результат не вычисляется:
float(subs(rewrite(fact2(n), gamma), n = 2^17))
|
Арифметическое выражение, представляющее целое число, больше, чем или равный - 1. |
Арифметическое выражение.
n