igammaНеполная гамма функция
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
igamma(a, x)
igamma(a, x) возвращает верхнюю неполную гамма функцию
.
Функция MATLAB® gammainc возвращает упорядоченный ниже неполная гамма функция: igamma(a, x) = gamma(a)(1 - gammainc(x, a)). Смотрите gamma и страницы ссылки на функцию gammainc в документации MATLAB.
Чтобы найти более низкую неполную гамма функцию для аргументов a и x, вычтите igamma(a, x) из gamma(a).
Значение с плавающей точкой возвращено, если по крайней мере один из аргументов является значением с плавающей точкой, и оба значения являются числовыми. В противном случае на символьные звонки igamma и/или других специальных функций можно ответить.
Следующие упрощения и переписывающие правила реализованы:
.
Для действительных численных значений a Type::Real, удовлетворяющего |a | ≤ Pref:: autoExpansionLimit (), функциональное отношение
используется рекурсивно, чтобы переключить первый аргумент к интервалу 0 ≤ a ≤ 1. Таким образом переписывание с точки зрения Ei, erfc и exp происходит, если a является целочисленным кратным
. Cf. Пример 1. Используйте expand, если эти преобразования также желаемы для |a |> Pref:: autoExpansionLimit ().
Специальное значение igamma(a, infinity) = 0 для
реализовано.
Когда названо аргументом с плавающей точкой, функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы демонстрируем некоторые вызовы с точными и символьными входными данными:
igamma(2, 3), igamma(1/7, x), igamma(sqrt(2), 3)
igamma(a, 4), igamma(1 + I, x^2 + 1), igamma(a, infinity)
Если первый аргумент a является действительным численным значением с |a | ≤ Pref:: autoExpansionLimit (), функциональные отношения используются рекурсивно, пока igamma не вызван первым аргументом от интервал 0 ≤ a ≤ 1:
igamma(-1/10, 1), igamma(7/4, 1)
Если первый аргумент является целочисленным кратным
, то полная перезапись с точки зрения Ei, erfc, и exp происходит:
igamma(-3, x), igamma(-5/2, x), igamma(8, x), igamma(13/2, 4)
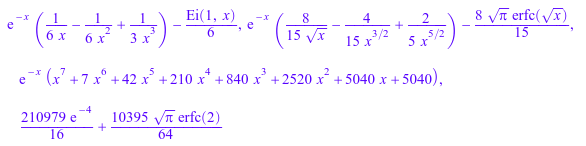
Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:
igamma(0.1, 4.0), igamma(7, 0.5), igamma(100, 100.0)
Функциональное отношение между igamma с различными первыми аргументами используется, чтобы “нормировать” возвращенные выражения:
igamma(-8, x), igamma(7/3, x)
|
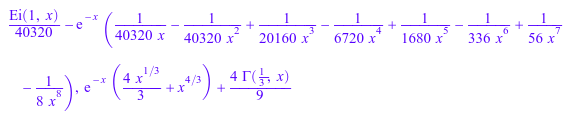
Арифметическое выражение.
a, x