psiФункция Digamma/polygamma
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
psi(x) psi(x,n)
psi(x) представляет дигамма-функцию, т.е. логарифмическую производную![]() функции
функции gamma.
psi(x, n) представляет n-th полигамма функция, т.е. n-th производная![]() .
.
psi(x, 0) эквивалентен psi(x).
Функция digamma/polygamma задана для всех сложных аргументов x кроме особых точек 0, - 1, - 2, ….
Если x является значением с плавающей точкой, то значение с плавающей точкой возвращено.
Упрощения реализованы для рациональных чисел x. В частности, если x = numer(x)/k со знаменателями k = 1, 2, 3, 4 или 6, явные результаты, выраженные с точки зрения ЭЙЛЕРА, PI и ln, возвращен. В целом, для любого рационального x с |x| (n + 1) ≤ 6 Pref::autoExpansionLimit() = 6000 (см. Pref::autoExpansionLimit), функциональное уравнение
![]() ,
,
используется, чтобы получить результат с аргументом x от интервала![]() . Используйте
. Используйте expand(psi(x, n)), чтобы получить такой сдвиг аргумента для больших значений x.
Некоторые явные формулы реализованы включая
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Специальные значения ψ (∞) = ∞ и![]() для n> 0 реализованы.
для n> 0 реализованы.
Для всех других аргументов возвращен символьный вызов функции psi.
Атрибут плавающий дигамма-функции, psi(x) является функцией ядра, т.е. оценкой с плавающей точкой, быстр. Атрибут плавающий полигамма функции psi(x, n) с n > 0 является библиотечной функцией. Обратите внимание на то, что psi(float(x)) и psi(float(x), n), а не float(psi(x)) и float(psi(x, n)) должны использоваться для оценки плавающей, потому что, для рациональных значений x, вычисления символьного результата psi(x), psi(x, n) может быть дорогостоящим. Далее, оценка плавающая символьного результата может быть численно нестабильной.
Атрибут expand использует функциональное уравнение
![]() ,
,
n th производная отражательной формулы
![]() ,
,
и формула умножения Gauß для того![]() , когда k является положительным целым числом, чтобы переписать
, когда k является положительным целым числом, чтобы переписать psi(x, n). Для числового x функциональное уравнение используется, чтобы переключить аргумент к области значений 0 < x < 1. Пример Cf. в качестве примера 3 и Пример 4.
Когда названо значением с плавающей точкой x, функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы демонстрируем некоторые вызовы с точными и символьными входными данными:
psi(-3/2), psi(4, 1), psi(3/2, 2)
![]()
psi(x + sqrt(2), 4), psi(infinity, 5)
![]()
Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:
psi(-5.2), psi(1.0, 3), psi(2.0 + 3.0*I, 10)
![]()
psi сингулярен для неположительных целых чисел:
psi(-2)
Error: Singularity. [psi]
Для положительных целых чисел и рациональных чисел x со знаменателями 2, 3, 4 и 6, соответственно, результат выражается с точки зрения ЭЙЛЕРА, PI, ln и zeta если |x| (n + 1) ≤ 6 Pref::autoExpansionLimit() = 6000:
Pref::autoExpansionLimit()
![]()
psi(-5/2), psi(-3/2, 1), psi(13/3, 2), psi(11/6, 4)

Для больших аргументов используйте expand, чтобы получить такие выражения:
psi(1001, 5)
![]()
expand(%)
6
8 PI
-----
63
- 133533.../1093808...Функции diff, expand, float, limit и series обрабатывают выражения, включающие psi:
diff(psi(x^2 + 1, 3), x), float(ln(3 + psi(sqrt(PI))))
![]()
expand(psi(2*x + 3, 2))
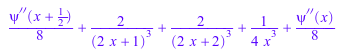
limit(x*psi(x), x = 0), limit(psi(x, 3), x = infinity)
![]()
series(psi(x), x = 0), series(psi(x, 3), x = infinity, 3)

| |
|
Неотрицательное целое число |
Арифметическое выражение.
x