Pref:: autoExpansionLimitУстановите предел для автоматических расширений
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Pref::autoExpansionLimit(n)
Pref::autoExpansionLimit(NIL)
Pref::autoExpansionLimit()
Pref::autoExpansionLimit(n) устанавливает предел для размера аргументов, до которых функции bernoulli, Ei, euler, fact, fact2, gamma, harmonic, igamma, psi и zeta приводят к явным результатам. Cf. Пример 1.
Это также устанавливает предел для экспоненты, до которой действительные и мнимые части степеней вычисляются явным образом. Cf. Пример 2.
Используйте expand для больших аргументов, если явные результаты желаемы. Cf. Пример 1.
Вызов Pref::autoExpansionLimit() возвращает текущее значение предела, не изменяя его.
Вызов Pref::autoExpansionLimit(NIL) сбрасывает предел своему значению по умолчанию 1000.
Функции bernoulli, euler, gamma, zeta и т.д. автоматически приводит к явным результатам, если аргументы не являются слишком большими:
bernoulli(22), euler(24), gamma(26), zeta(28)

Эти функции дают символьные ответы, когда аргумент больше, чем предел, установленный Pref::autoExpansionLimit:
Pref::autoExpansionLimit()
![]()
bernoulli(1002), euler(2002), gamma(3001), zeta(4001)
![]()
Мы уменьшаем этот предел:
Pref::autoExpansionLimit(20):
bernoulli(22), euler(24), gamma(26), zeta(28)
![]()
Мы можем использовать expand, чтобы получить явные результаты:
expand(bernoulli(22)), expand(euler(24)), expand(gamma(26)), expand(zeta(28))

Мы восстанавливаем значение по умолчанию:
Pref::autoExpansionLimit(NIL):
Если разложение по формуле бинома необходимо, закрытая формула для действительной части выражения может стать довольно большой:
Re((a+sqrt(2)*I)^6) assuming a in R_
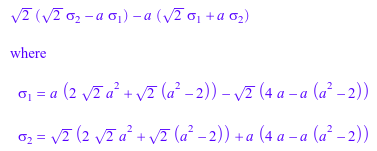
Таким образом, для экспонент вне Pref::autoExpansionLimit(), никакое расширение не выполняется:
Re((a+sqrt(2)*I)^123456) assuming a in R_
![]()
|
Предел: положительное числовое действительное значение |
Ранее заданный предел.