monomialsОтсортированный список одночленов полинома
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
monomials(p, <order>) monomials(f, <vars>, <order>)
monomials(p, order) возвращает список ненулевых одночленов полиномиального p. Список сортируется относительно термина, заказывая order.
monomials возвращает список всех нетривиальных одночленов данного полинома. Одночлены сортируются согласно термину данное упорядоченное расположение. Список пуст, если полином является нулем.
Многочленное выражение f сначала преобразовано в полином с переменными, данными vars. Если никакие переменные не даны, они разыскиваются в f. Смотрите poly о деталях преобразования. Результат возвращен как список многочленных выражений. FAIL возвращен, если f не может быть преобразован в полином.
Результат monomials не полностью оценен. Это может быть оценено функциями mapcoeffs и eval. Cf. Пример 4.
Мы даем некоторым сам объяснение примеров:
p := poly(100*x^100 + 49*x^49 + 7*x^7, [x]): monomials(p)
![]()
monomials(poly(0, [x]))
![]()
delete p:
Мы демонстрируем эффект различных порядков термина:
p := poly(5*x^4 + 4*x^3*y*z^2 + 3*x^2*y^3*z + 2, [x, y, z]): monomials(p)

monomials(p, DegreeOrder)
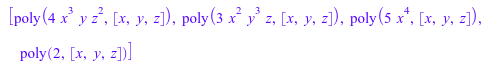
monomials(p, DegInvLexOrder)

delete p:
Этот пример показывает определяемое пользователем упорядоченное расположение термина. Здесь мы используем противоположный лексикографический порядок на 3 indeterminates:
order := Dom::MonomOrdering(RevLex(3)): p := poly(5*x^4 + 4*x^3*y*z^2 + 3*x^2*y^3*z + 2, [x, y, z]): monomials(p, order)
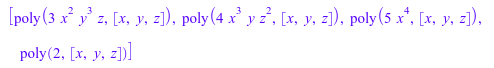
delete order, p:
Мы демонстрируем стратегию оценки monomials:
p := poly(3*x^3 + 6*x^2*y^2 + 2, [x]): y := 4: monomials(p)
![]()
Оценка осуществляется eval:
map(%, mapcoeffs, eval)
![]()
delete p, y:
| |
| |
|
Список indeterminates полинома: обычно, идентификаторы или индексированные идентификаторы |
|
Термин упорядоченное расположение: |
Список полиномов того же типа как p. Список выражений возвращен, если выражение дано. Список пуст, если полином является нулем.
p